 |
Главная |
Составление уравнений состояния цепи
|
из
5.00
|
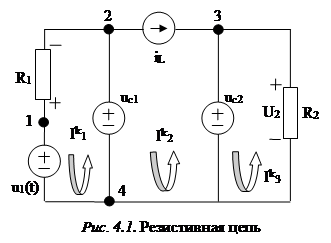
Для составления уравнений состояния цепи воспользуемся методом вспомогательных источников: заменим индуктивные элементы источниками тока, а конденсаторы – источниками напряжения (Рис. 4.1.). Расчет получившейся резистивной цепи будем осуществлять методом контурных токов (МКТ):
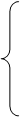 |
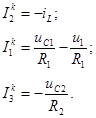
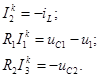
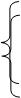
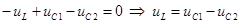
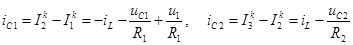
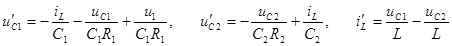
Уравнения состояния:
Произведем машинный расчет характеристического полинома цепи:
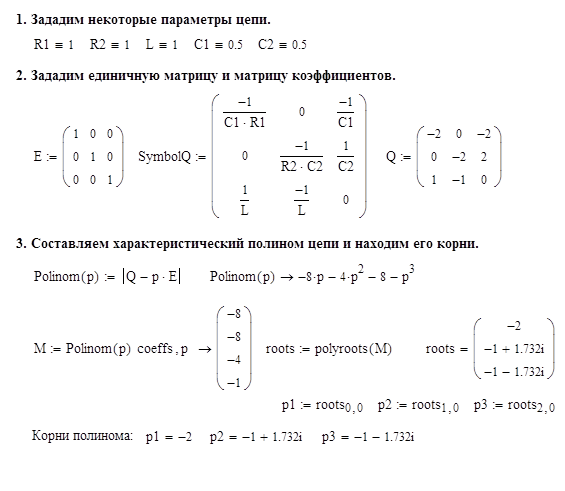
Проконтролируем полученные результаты способом, описанным в [3, стр. 28]:
1. Корни характеристического полинома цепи совпали с корнями знаменателя передаточной функции, который согласно [1, стр. 157] также является характеристическим полиномом цепи.
2. Рассмотрим эквивалентные схемы замещения исходной цепи (Рис. 4.2).
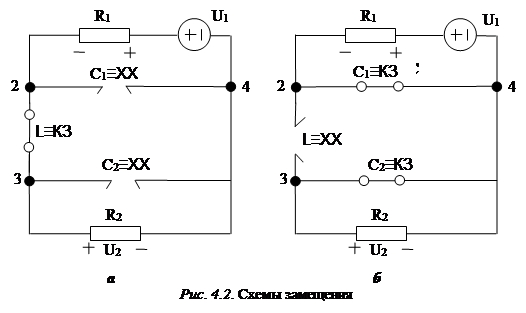
Случай а - вынужденный режим ( 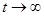 ):
): 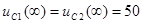 ,
, 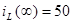 . Такие же вынужденные значения получаем по уравнениям состояния цепи, приравняв левую их часть к нулю.
. Такие же вынужденные значения получаем по уравнениям состояния цепи, приравняв левую их часть к нулю.
Случай б ( 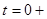 ):
): 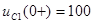 ,
,  ,
, 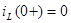 .
.
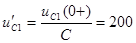 ,
, 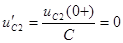 ,
, 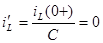 .
.
Такие же значения производных получаем из уравнений состояния при 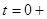 .
.
Проведенная проверка позволяет говорить о правильности полученного выше результата.
5. Определение переходной  и импульсной
и импульсной 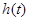 характеристик
характеристик
Согласно [1, стр. 156] передаточная функция цепи 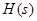 есть изображение по Лапласу импульсной характеристики цепи
есть изображение по Лапласу импульсной характеристики цепи 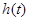 :
:
H(s) ¸h(t)
Также исходя из [1, стр. 156], переходная характеристика цепи 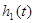 определяется из выражения:
определяется из выражения:
h1(t) ¸H1(s)=H(s)/s
Таким образом, импульсную и переходную характеристики цепи можно найти, взяв оригинал от изображения 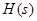 и
и 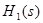 соответственно (для этого следует использовать теорему разложения, описанную в [1, стр. 140]). Произведем машинный расчет для данного случая (при этом необходимо полученный результат домножить на
соответственно (для этого следует использовать теорему разложения, описанную в [1, стр. 140]). Произведем машинный расчет для данного случая (при этом необходимо полученный результат домножить на 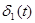 для
для 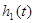 , на
, на 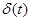 для
для 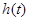 ):
):
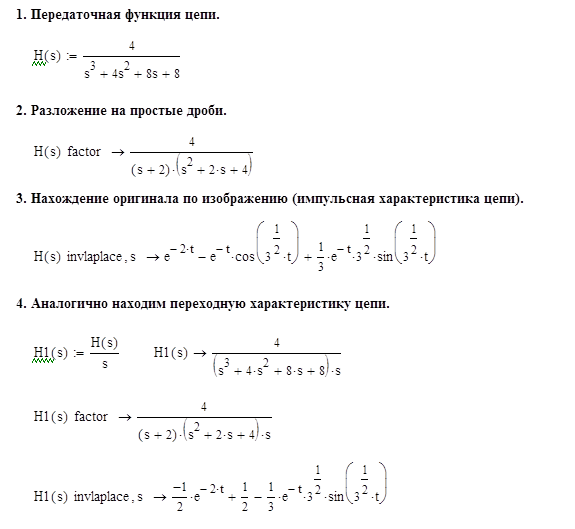
Проконтролируем полученные результаты способом, описанным в [3, стр. 33]: контролю подвергнем конечное и начальное значения полученной переходной характеристики, использовав теоремы о конечном и начальном значении:
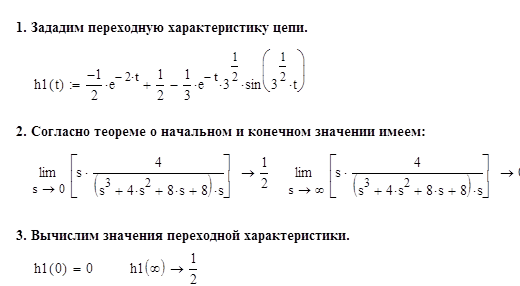
Условие совпадения 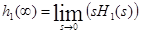 и
и 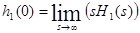 выполнено, что позволяет говорить о правильности полученного выше результата.
выполнено, что позволяет говорить о правильности полученного выше результата.
Построим графики переходной (Рис. 5.2) и импульсной (Рис. 5.1) характеристик цепи, изобразив на графиках кроме этого еще и составляющие аналитического расчета этих характеристик (см. следующий лист).
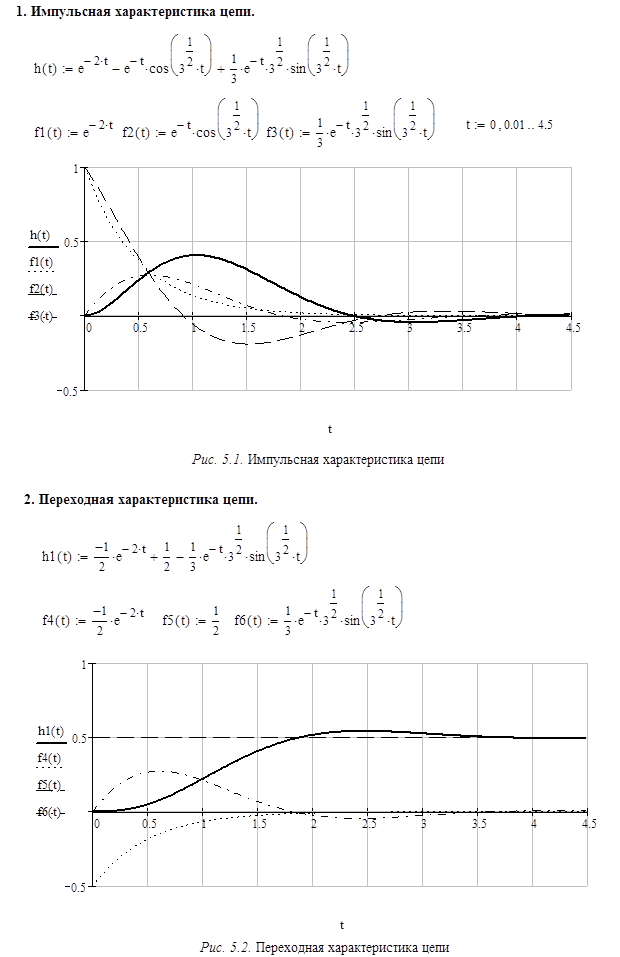
Согласно Рис. 5.2. длительность переходного процесса составляет примерно 3, что согласуется с нашими предположениями о значении данной величины в п.2 курсового расчета (см. выше).
Найдем теперь переходную и импульсную характеристики цепи по уравнениям состояния, полученным в п. 4 курсового расчета. Входное воздействие: 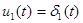 , начальные условия – нулевые. Рассчитаем по полученным в п.4 уравнениям состояния реакцию – выходное напряжение
, начальные условия – нулевые. Рассчитаем по полученным в п.4 уравнениям состояния реакцию – выходное напряжение 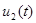 . Запишем сначала уравнения состояния в матричной форме:
. Запишем сначала уравнения состояния в матричной форме:
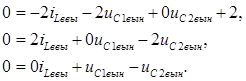
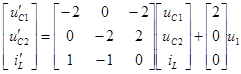
Общий вид уравнения: 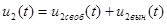 . Вынужденную составляющую решения находим из уравнений состояния, приведенных выше, приравняв левую часть к нулю. Приняв во внимание, что
. Вынужденную составляющую решения находим из уравнений состояния, приведенных выше, приравняв левую часть к нулю. Приняв во внимание, что 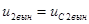 , проведем машинный расчет для данного случая:
, проведем машинный расчет для данного случая:
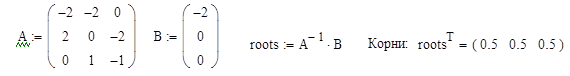
Таким образом, 
Свободная составляющая решения:  . Частоты
. Частоты 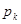 собственных колебаний согласно [1, стр. 157] есть корни характеристического полинома, которые были найдены в п. 4 курсового расчета. Длительность переходного процесса:
собственных колебаний согласно [1, стр. 157] есть корни характеристического полинома, которые были найдены в п. 4 курсового расчета. Длительность переходного процесса: 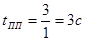 . Найдем теперь постоянные интегрирования
. Найдем теперь постоянные интегрирования 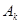 , для чего определим начальные значения
, для чего определим начальные значения 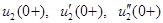 .
.
Начальное значение по закону коммутации 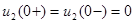 . Начальное значение первой производной найдем по одному из уравнений состояния:
. Начальное значение первой производной найдем по одному из уравнений состояния: 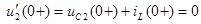 .
.
Начальное значение второй производной: 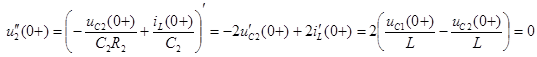
Для определения постоянных интегрирования решим систему уравнений:
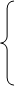 |
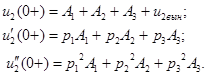
Машинный расчет корней данной системы уравнений:
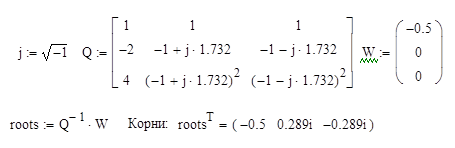
Таким образом, значение постоянных интегрирования 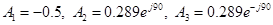 .
.
Получаем реакцию:
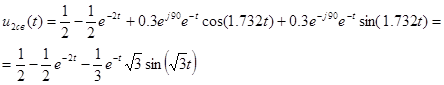
Таким образом: 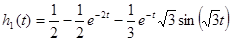 .
.
Для получения импульсной характеристики цепи 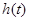 продифференцируем переходную характеристику:
продифференцируем переходную характеристику:
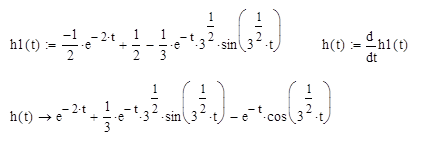
Данные выражения, что и следовало ожидать, совпадают с результатами расчета по Лапласу переходной и импульсной характеристики цепи.
|
из
5.00
|
Обсуждение в статье: Составление уравнений состояния цепи |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

