 |
Главная |
Аналитическое описание алгоритма вычислений
|
из
5.00
|
Имитационное моделирование стохастических систем основано на реализации алгоритмов, воспроизводящих процесс функционирования системы во времени. При этом имитируются элементарные явления, составляющие процесс. Как правило, эти явления носят случайный характер, что и определяет необходимость получения случайных чисел. При этом имеется в виду два основных аспекта имитационного моделирования с применением вычислительных машин :
- необходимость генерирования с помощью специальных программных средств равномерно распределенных псевдослучайных чисел;
-использование этих случайных чисел для программной генерации случайных величин с требуемыми параметрами и характеристиками.
Базовым генератором для получения последовательностей случайных чисел, является генератор равномерно распределенной случайной величины на интервале (0,1). Такая непрерывная случайная величина Х имеет функцию распределения
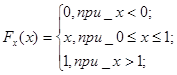
и функцию плотности распределения вероятности

Датчик случайных чисел, основанный на использовании алгоритма Лемера, является частным случаем линейного метода (наиболее широко применяемый в настоящее время программный генератор равномерно распределенных чисел):

где  , а также получаемые случайные числа
, а также получаемые случайные числа  являются целыми числами. Образование равномерно распределенных чисел на интервале (0,1) реализуется с помощью выражения
являются целыми числами. Образование равномерно распределенных чисел на интервале (0,1) реализуется с помощью выражения

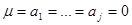
и полагая, что  получаем
получаем

В алгоритме Лемера задаются два соответствующим образом подобранных целых числа: множитель a и модуль m. Последовательность случайных чисел вычисляется следующим образом.
1) Число  известно с предыдущего шага. Вычисляется произведение
известно с предыдущего шага. Вычисляется произведение  .
.
2) Число  делится на m. Получается целое число и целочисленный остаток
делится на m. Получается целое число и целочисленный остаток  , что можно представить в виде:
, что можно представить в виде:


3) Так как  является числом между 0 и m, то нужно его еще раз разделить на m, чтобы получить число между 0 и 1 , то есть
является числом между 0 и m, то нужно его еще раз разделить на m, чтобы получить число между 0 и 1 , то есть

Последовательность случайных чисел, полученные мультипликативным методом, периодически повторяются.
Наиболее часто встречающимся видом распределения является нормальное распределение. В связи с этим при моделировании различных явлений возникает потребность иметь в распоряжении последовательность случайных чисел, отвечающих нормальному закону распределения с функцией плотности

где m- математическое ожидание,
σ- среднеквадратичное отклонение.
 Случайная величина с нормальным распределением N(0,1) может быть реализована с помощью классических общих методов моделирования. Кроме этих методов разработаны специальные методы, позволяющие получать с большой скоростью достаточно длинные последовательности случайных чисел, отвечающих нормальному закону распределения N(µ,σ2) с математическим ожиданием m=µ и дисперсией D= σ2. Реализация выполняется в два этапа:
Случайная величина с нормальным распределением N(0,1) может быть реализована с помощью классических общих методов моделирования. Кроме этих методов разработаны специальные методы, позволяющие получать с большой скоростью достаточно длинные последовательности случайных чисел, отвечающих нормальному закону распределения N(µ,σ2) с математическим ожиданием m=µ и дисперсией D= σ2. Реализация выполняется в два этапа:
1) Выполняют реализацию случайной величины с плотностью N(0,1):x1,x2,…,xn;
2) При помощи линейного преобразования

получают последовательность случайных чисел, отвечающих распределению N(µ,σ2): у1,у2,…,уn.
Один из самых известных методов программной реализации нормально распределенной случайной величины основан на центральной теореме: распределение суммы независимых случайных величин приближается к нормальному при неограниченном увеличении n, если выполняются следующие условия:
1) все эти величины имеют конечные математические ожидания и дисперсии;
2) ни одна из величин по своему значению резко не отличается от всех остальных.
Согласно этой теореме можно сконструировать алгоритм реализации случайной величины Х на основе аппроксимации распределения N(0,1) суммой независимых случайных величин R1,R2,…,Rn, равномерно распределенной на интервале [0,1). Так как каждая из них имеет математическое ожидание M(Ri)=1/2 и дисперсию D(Ri)=1/12, i=1,2,…,n, то

Согласно центральной предельной теореме распределение случайной величины

при достаточно больших n приближается к N(0,1). Практика показывает , что при n=12 аппроксимация уже удовлетворительна. Тогда формула принимает вид :

 Алгоритм
Алгоритм

Описание форматов SFR
1. Регистр режима таймера/счётчика TMOD:
| М1 | М0 |
Биты М1 и М0 определяют режим работы таймера/счётчика:
| М1 | М0 | |
| 0 | 0 | Режим 0 |
| 0 | 1 | Режим 1 |
| 1 | 0 | Режим 2 |
| 1 | 1 | Режим 3 |
В режиме 0 TL0 работает как 5-битный предделитель частоты.
Режим 1 – 16-битный таймер-счётчик. TH0 и TL0 включены последовательно.
Режим 2 – 8-битный автоперезагружаемый таймер/счётчик. TH0 хранит значение, которое должно быть перезагружено в TL0 каждый раз по переполнению.
Режим 3 – таймер/счётчик 1 останавливается. Таймер/счётчик: TL0 работает как 8-битный таймер/счётчик, и его режим определяется управляющими битами таймера 0. TH0 работает только как 8-битный таймер, и его режим определяется управляющими битами таймера 1 .
Установим таймер/счётчик 0 в режим 1: загружаем в регистр TMOD #01H.
2. Регистр масок прерывания IE.
| EA | ET0 |
EA (IE.7) – снятие блокировки прерываний. Сбрасывается программно для запрета всех прерываний независимо от состояний IE4 – IE0.
ET0 – бит разрешения прерывания от таймера 1. Установка/сброс программой для разрешения/запрета прерываний.
(IE)=82h.
3. Регистр управления/статуса таймера TCON.
| TR0 |
TR0 – бит управления таймера 0. Устанавливается/сбрасывается программой для пуска/остановки таймера/счётчика.
(TCON)=10H.
4. Таймер/счётчик 0: регистр TL0 – младший байт,
регистр TH0 – старший байт.
Коды, загружаемые в эти регистры, выбираются исходя из частоты дискретизации. Частота дискретизации hд в данной работе принимается равной 100 Гц. Следовательно, прерывания будут происходить через каждые 10 мс.
1000010=271016.
10000h-2710h=0D8F0h.
Кроме того, необходимо учесть количество импульсов, которое поступит на вход счётчика к моменту записи в него младшего байта (допустим это составит 12мкс) и время, потраченное на переход от запроса прерывания к его обработке, например, 9мкс:
0D8F0H+2110=0D905h.
(TL0)=05h, (TH0)=0D9h.
|
из
5.00
|
Обсуждение в статье: Аналитическое описание алгоритма вычислений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

