 |
Главная |
Геометрия Лобачевского в реальном мире.
|
из
5.00
|
Если геометрия Евклида является только частью геометрии Лобачевского, то выходит, что наш мир – не мир Евклида, как принято считать? Почему же мы не замечаем разницы?
Как пример можно привести тот факт, что видимый звездный свод это ни что иное, как предельная плоскость. Астрономам после признания достижений Лобачевского пришлось пересчитывать все расстояния между звездами – и ошибки достигали 1/6.
 Но вернемся на землю. Есть такое понятие – гауссова кривизна пространства. Если мы возьмем кривую поверхность, проведем к какой-то точке касательную, проведем в точку касания отрезок, перпендикулярный касательной плоскости, то мы получим нормаль. Проведя через нормаль плоскость, мы можем найти окружность, наиболее плотно прилегающую к поверхности. Так как мы можем провести сколько угодно плоскостей, то мы можем найти окружности с минимальным и максимальным радиусом. Подставив их в выражение
Но вернемся на землю. Есть такое понятие – гауссова кривизна пространства. Если мы возьмем кривую поверхность, проведем к какой-то точке касательную, проведем в точку касания отрезок, перпендикулярный касательной плоскости, то мы получим нормаль. Проведя через нормаль плоскость, мы можем найти окружность, наиболее плотно прилегающую к поверхности. Так как мы можем провести сколько угодно плоскостей, то мы можем найти окружности с минимальным и максимальным радиусом. Подставив их в выражение  , мы получим Гауссову кривизну пространства. Если К>0, то поверхность в этой точке эллиптическая. Если К<0, то гиперболическая. Если К=0, то параболическая.
, мы получим Гауссову кривизну пространства. Если К>0, то поверхность в этой точке эллиптическая. Если К<0, то гиперболическая. Если К=0, то параболическая.
Как мы уже знаем, на поверхностях с отрицательной кривизной работает геометрия Лобачевского. Но именно такую кривизну имеют графики интенсивности всех электромагнитных полей! Состояние поверхности плазмы также описывается геометрией Лобачевского.
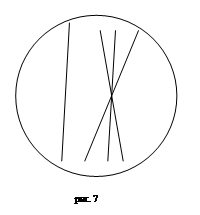
Но наглядно геометрию Лобачевского можно устроить и на бумаге. Если нарисовать окружность, то мы можем, не выходя за её пределы, провести сколько угодно прямых, не пересекающих данную (рис. 7). Взяв сферу, можно построить стереометрическую модель. Такая модель называется моделью Клейна.
Все эти модели служат одной цели – полнее представить наш мир, не прибегая к вселенским масштабам.
Заключение.
Когда Евклид формулировал пятый постулат, вряд ли он знал, какую бурю тот вызовет. Когда Лобачевский отказался от пятого постулата, он не знал, что его «воображаемая геометрия» на поверку окажется реальной.
Нельзя сказать, что неевклидова геометрия единственно правильна. На данный момент к ней нет никаких претензий. Но, может быть, через много лет она устареет – или это произойдет быстрее? Так или иначе, но наука никогда не будет стоять на месте, и когда – нибудь и этот проект окажется макулатурой.
Но думаю, что этого времени он успеет исполнить свое предназначение – рассказать и заинтересовать читателя настоящей геометрией нашего мира. Именно из-за популярного характера в нем нет ни строгих доказательств, ни полного описания неевклидовой геометрии. Но для поверхностного ознакомления с ней он вполне годен.
Приложение.
 При доказательства используют рисунок 1. Пусть ОХ перпендикулярно ОY.
При доказательства используют рисунок 1. Пусть ОХ перпендикулярно ОY.
 Через точку А прямой ОY проведем прямую АА’ , параллельную ОХ, и построим предельную линию с осью ОХ, проходящую через точку О. Дугу
Через точку А прямой ОY проведем прямую АА’ , параллельную ОХ, и построим предельную линию с осью ОХ, проходящую через точку О. Дугу  , заключенную между осями ОХ и АА’, обозначим через s, отрезки ОА и АВ – соответственно через u и v. Проведем прямую ММ’, параллельную ОХ и ОY. Предельную дугу ОС, заключенную между ОХ и ММ’, обозначим через s. Нашей задачей является вывод следующих формул:
, заключенную между осями ОХ и АА’, обозначим через s, отрезки ОА и АВ – соответственно через u и v. Проведем прямую ММ’, параллельную ОХ и ОY. Предельную дугу ОС, заключенную между ОХ и ММ’, обозначим через s. Нашей задачей является вывод следующих формул:  (А) и
(А) и  (В).
(В).
Построим прямую NN’, параллельную ОY и перпендикулярную АА’, и через точку N проведем предельную дугу  , концентрическую дуге
, концентрическую дуге 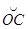 . Так как прямая М’М параллельна NN’ и АА’, то NР = s. Далее, так как ÐОАА’ = П(u)*, Ð YАN, то АN = u, т.е. NВ = u + v. Применяя формулу
. Так как прямая М’М параллельна NN’ и АА’, то NР = s. Далее, так как ÐОАА’ = П(u)*, Ð YАN, то АN = u, т.е. NВ = u + v. Применяя формулу  к концентрическим дугам
к концентрическим дугам  = s и
= s и 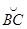 = s - s, получаем
= s - s, получаем  (3). Отложим теперь отрезок ОА = u и проведем прямую АА’, параллельную ОХ, и прямую ММ’, параллельную ОХ и ОY. Строим прямую NN’, перпендикулярную АА’ и параллельную ОY (рис. 2). Через точку О проведем ортогонально к ОХ предельную дугу
(3). Отложим теперь отрезок ОА = u и проведем прямую АА’, параллельную ОХ, и прямую ММ’, параллельную ОХ и ОY. Строим прямую NN’, перпендикулярную АА’ и параллельную ОY (рис. 2). Через точку О проведем ортогонально к ОХ предельную дугу  = s + s, через точку N – концентрическую дугу
= s + s, через точку N – концентрическую дугу  = s. Так как Ð ОАА’ = П(ОА) = П(АN), то АN = ОА = u, т.е. ВN = u – v. Итак,
= s. Так как Ð ОАА’ = П(ОА) = П(АN), то АN = ОА = u, т.е. ВN = u – v. Итак, 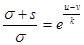 (4). Складывая отношения (3) и (4), получаем формулу (А). вычитая (3) из (4), имеем
(4). Складывая отношения (3) и (4), получаем формулу (А). вычитая (3) из (4), имеем  . Подставляя сюда из (А)
. Подставляя сюда из (А)  , получаем соотношение (В).
, получаем соотношение (В).
*Имеется ввиду, что отрезок u определяется углом параллельности ÐОАА’ .
**Гиперболические функции определяются так:
1. Синус: 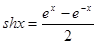 .
.
2. Косинус:  .
.
3. Тангенс:  .
.
Использованная литература.
Смилга В.П. В погоне за красотой./. Н-п издание. – М.: Молодая гвардия, 1968. – 200 стр. с илл.
Колесников М. Лобачевский./. Серия «Жизнь замечательных людей». – М.: Молодая гвардия, 1965. – 320 стр. с илл.
Широков П.А. Краткий очерк основ геометрии Лобачевского./. – М.: Наука, 1983. – 76 стр.
|
из
5.00
|
Обсуждение в статье: Геометрия Лобачевского в реальном мире. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

