Аффинные преобразования

 

Цель работы: изучение алгоритмов параллельного сдвига, растяжения – сжатия и поворота графического объекта на плоскости и в пространстве.

Любое преобразование объектов представляется как сумма элементарных действий. Рассмотрим частные случаи аффинного преобразования. На рисунках 7.1–7.3 представлены эти действия и соответствующая матрица преобразования.

 

0

dx

x

dy

y

0

X

Y

Рисунок 7.1 – Параллельный сдвиг координат

 

 

Система уравнений	Матрица преобразования

 

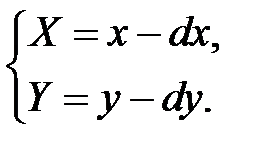
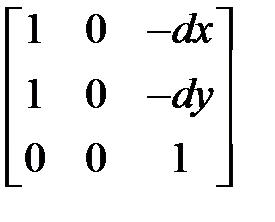
0

x

y

X

Y

Рисунок 7.2 – Растяжение-сжатие осей координат

 

Система уравнений	Матрица преобразования

 

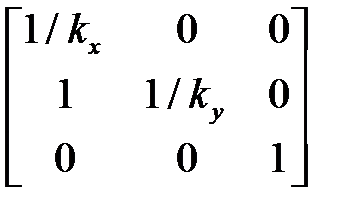
Коэффициенты k_x и k_y могут быть отрицательными. Например, k_x = –1, что соответствует зеркальному отражению относительно оси у.

 

 

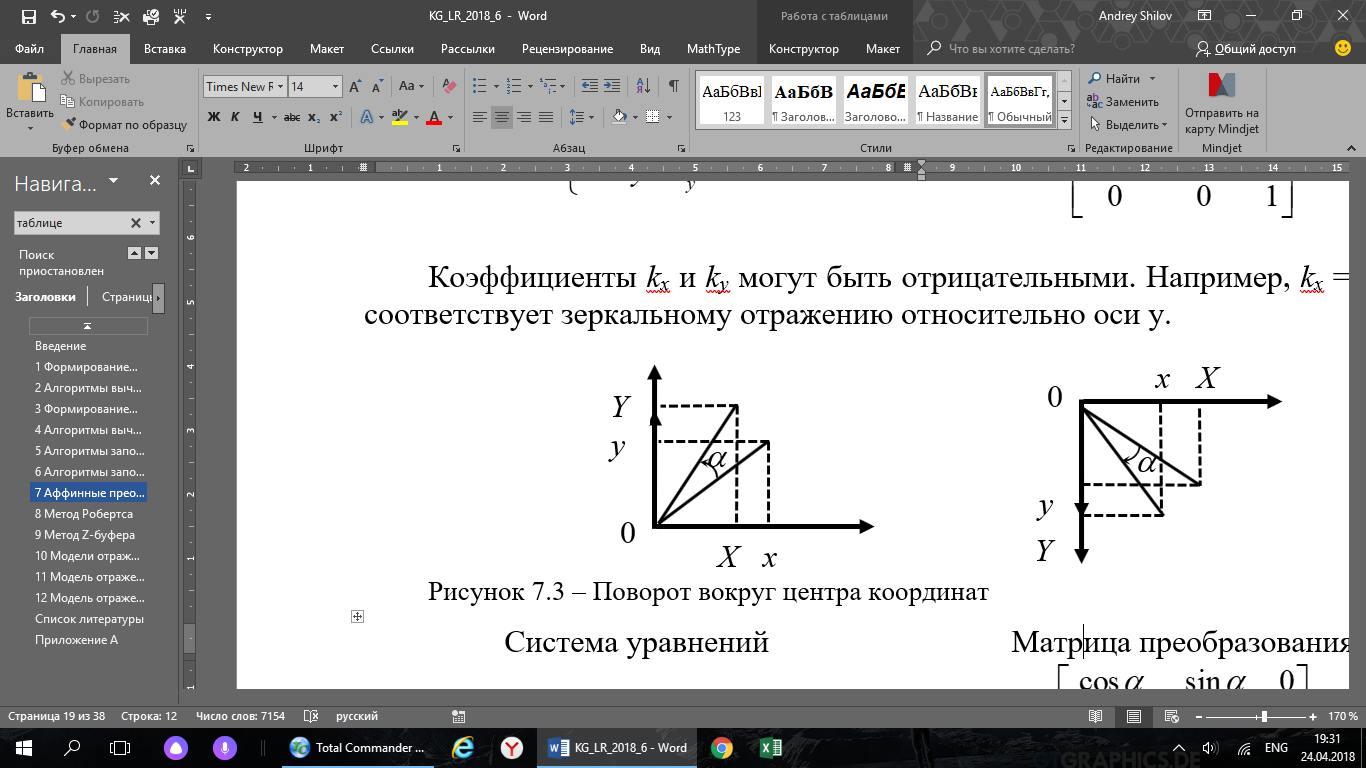
Рисунок 7.3 – Поворот вокруг центра координат

Система уравнений

Матрица преобразования

 

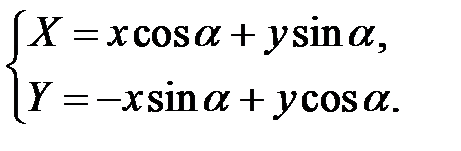
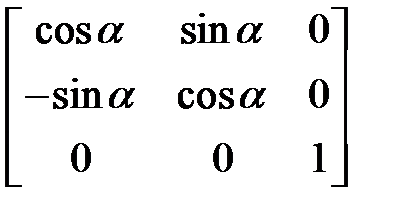
Практическое задание.

 

Составить алгоритм и программу для перемещения, сжатия-растяжения и поворота объекта № 1. При разработке программы умножение матриц производить с помощью соответствующей подпрограммы, без использования функций листа.

Содержание отчета: блок-схема данной программы; краткие ответы на вопросы, приведенные в таблице 7.1; распечатка листа Excel с результатами.

 

Таблица 7 – Вопросы для защиты

 

Вопросы	Рейтинг
Какие преобразования координат называют «аффинными»	1
Записать линейные преобразования в матричной форме	1
Привести формулу для вычисления элементов матрицы С=А*В	1
Привести формулы параллельного сдвига координат точки	1
Привести формулы растяжение-сжатие координат точки	1
Привести формулы для поворота координат точки	1
Перечислить свойства аффинного преобразования	1
Пояснить схему алгоритма преобразования координат в плоскости	2

 

Метод Робертса

 

Цель работы: изучение алгоритма удаления невидимых граней методом Робертса.

Алгоритм Робертса представляет собой первое известное решение задачи об удалении невидимых линий. Это математически элегантный метод, работающий в объектном пространстве. Алгоритм прежде всего удаляет из каждого тела те ребра или грани, которые экранируются самим телом.

Пусть F – некоторая грань многогранника. Плоскость, несущая эту грань, разделяет пространство на два подпространства. Назовем положительным то из них, в которое смотрит внешняя нормаль к грани. Если точка наблюдения – в положительном подпространстве, то грань – лицевая, в противном случае – нелицевая. Если многогранник выпуклый, то удаление всех нелицевых граней полностью решает задачу визуализации с удалением невидимых граней.

Для определения, лежит ли точка в положительном подпространстве, используют проверку знака скалярного произведения , где 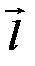 – вектор, направленный к наблюдателю, фактически определяет точку наблюдения;  – вектор внешней нормали грани. Если  > 0, т. е. угол между векторами острый, то грань является лицевой. Если  < 0, т. е. угол между векторами тупой, то грань является нелицевой.

В алгоритме Робертса требуется, чтобы все изображаемые тела или объекты были выпуклыми. Невыпуклые тела должны быть разбиты на выпуклые части. В этом алгоритме выпуклое многогранное тело с плоскими гранями должно представиться набором пересекающихся плоскостей. Уравнение произвольной плоскости в трехмерном пространстве имеет вид

 

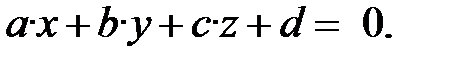                           (8.1)

 

В матричной форме этот результат выглядит так:

 

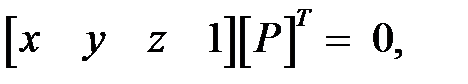                        (8.2)

 

где [P]^T = [a b c d] представляет собой плоскость. Поэтому любое выпуклое твердое тело можно выразить матрицей тела, состоящей из коэффициентов уравнений плоскостей, т. е.

 

                             (8.3)

 

где каждый столбец содержит коэффициенты одной плоскости.

Напомним, что любая точка пространства представима в однородных координатах вектором [S] = [х у z 1]. Более того, если точка [S] лежит на плоскости, то [S]·[P]^T = 0. Если же [S] не лежит на плоскости, то знак этого скалярного произведения показывает, по какую сторону от плоскости расположена точка. В алгоритме Робертса предполагается, что точки, лежащие внутри тела, дают отрицательное скалярное произведение, т. е. нормали направлены наружу. Чтобы проиллюстрировать эти идеи, рассмотрим следующий пример. Рассмотрим единичный куб с центром в начале координат (рисунок 8.1).

 

 

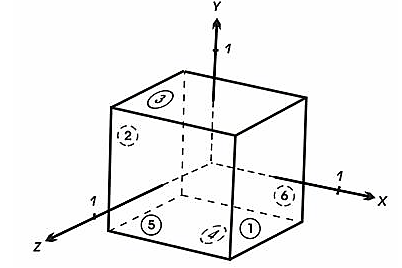
Рисунок 8.1 – Куб с центром в начале координат

 

Шесть плоскостей, описывающих данный куб, таковы:

 

x₁ = 1/2, x₂ = –1/2, y₃ = 1/2, y₄ = –1/2, z₅ = 1/2, z₆ = –1/2.

 

Более подробно уравнение правой плоскости можно записать как

x₁ + 0×y₁ + 0×z₁ – (1/2) = 0 или 2x₁ – 1 = 0.

 

Полная матрица тела такова:

 

  (8.4)

 

Экспериментально проверим матрицу тела с помощью точки, о которой точно известно, что она лежит внутри тела. Если знак скалярного произведения для какой-нибудь плоскости больше нуля, то соответствующее уравнение плоскости следует умножить на –1. Для проверки возьмем точку внутри куба с координатами x = 1/4, y = 1/4, z = 1/4. В однородных координатах эта точка представляется в виде вектора

 

[S] = [1/4 1/4 1/4 1] = [1 1 1 4].

 

Скалярное произведение этого вектора на матрицу объема равно

 

 

 

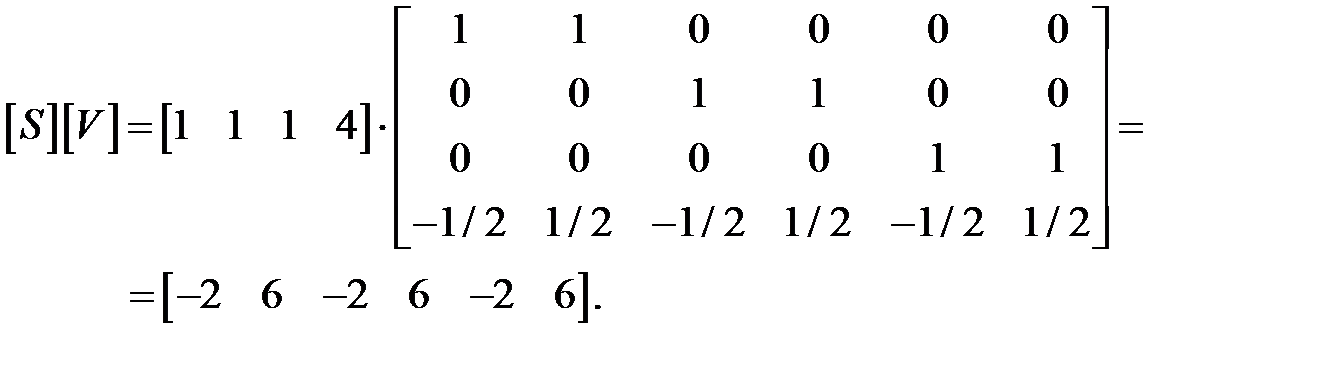
Здесь результаты для второго, четвертого и шестого уравнения плоскостей (столбцов) положительны и, следовательно, составлены некорректно. Умножая эти уравнения (столбцы) на –1, получаем корректную матрицу тела для куба:

 

.

 

В приведенном примере корректность уравнений плоскостей была проверена экспериментально. Разумеется, это не всегда возможно. Существует несколько полезных методов для более общего случая. Хотя уравнение плоскости содержит четыре неизвестных коэффициента, его можно нормировать так, чтобы d = 1. Следовательно, трех неколлинеарных точек достаточно для определения этих коэффициентов. Нормированное уравнение в матричной форме при подстановке координат трех неколлинеарных точек (x₁, y₁, z₁), (x₂, y₂, z₂), (х₃, у₃, z₃) имеет следующий вид:

 

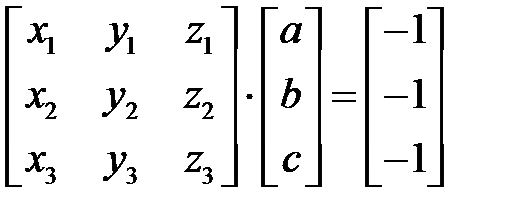 или 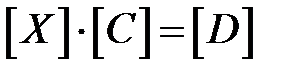.      (8.5)

 

Решение этого уравнения дает значения коэффициентов уравнения плоскости:

 

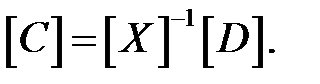                                       (8.6)

 

Другой способ используется, если известен вектор нормали к плоскости, т. е. 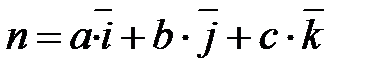 , где i, j, k – единичные векторы осей х, у, z соответственно. Тогда уравнение плоскости примет вид  .

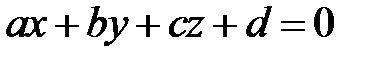Перед началом работы алгоритма удаления невидимых линий или поверхностей для получения желаемого вида сцены часто применяется трехмерное видовое преобразование. Матрицы тел для объектов преобразованной сцены можно получить преобразованием исходных матриц тел.

Если [T] – матрица размером 4 x 4 видового преобразования, то
[VT] = [T]^-1[V].

Итак, преобразованная матрица тела получается умножением исходной матрицы тела слева на обратную матрицу видового преобразования.

Тот факт, что плоскости имеют бесконечную протяженность и что скалярное произведение точки (вектора к точке) на матрицу тела положительно, если точка лежит вне этого тела, позволяет предложить метод, в котором матрица тела используется для определения граней, которые экранируются самим этим телом.

Положительное скалярное произведение дает только такая плоскость (столбец) в матрице тела, относительно которой точка лежит снаружи, т. е. в положительном подпространстве.

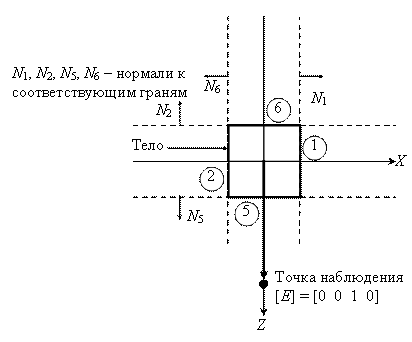
Рисунок 8.2 – Точка наблюдения вне тела

 

Условие [Е]·[V] < 0 определяет, что плоскости – нелицевые, а их грани – задние. Заметим, что для аксонометрических проекций (точка наблюдения в бесконечности) это эквивалентно поиску положительных значений в третьей строке матрицы тела. Найдем произведение [Е]·[V] для нашего примера (см. рисунок 8.2):

 

 

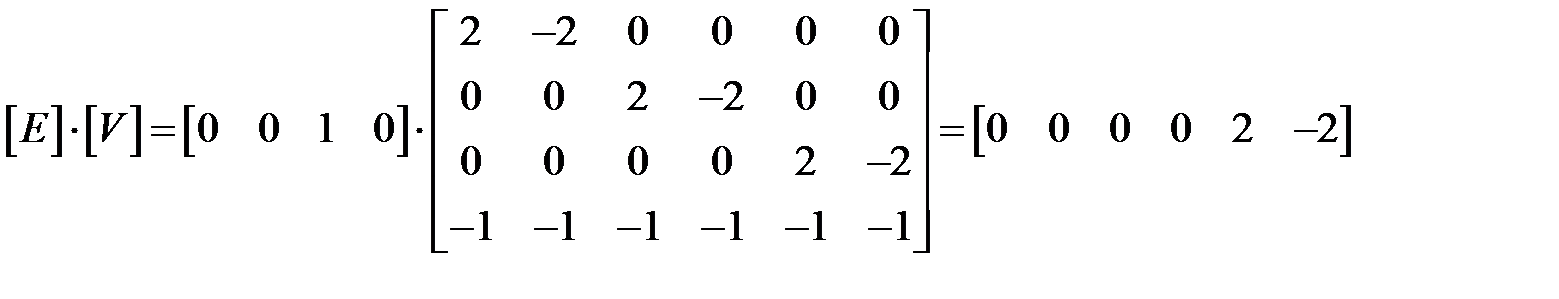
Отрицательное число в шестом столбце показывает, что грань с этим номером нелицевая. Положительное число в пятом столбце показывает, что грань лицевая. Нулевые результаты соответствуют плоскостям, параллельным направлению взгляда.

Положительный результат вектора E и вектора нормали можно интерпретировать как острый угол между этими векторами, отрицательный результат – как тупой угол. Если угол между векторами острый, то грань является лицевой; если угол тупой, то грань – нелицевая.

 

Практическое задание

 

Составить алгоритм и программу для поворота объекта № 3 вокруг вертикальной оси 0Z. При разработке программы умножение матриц производить с помощью соответствующей подпрограммы, без использования функций листа.

Содержание отчета: блок-схема данной программы; краткие ответы на вопросы, приведенные в таблице 8.1; распечатка листа Excel с результатами.

 

Таблица 8.1 – Вопросы для защиты

 

Вопрос	Рейтинг
Привести уравнение плоскости в трехмерном пространстве в алгебраическом и матричном виде	1
Привести пример и пояснить создание матрицы выпуклого тела	1
Как определяется, с какой стороны плоскости находится точка с координатами X 0, Y 0, Z 0	1
Привести формулы видового преобразования тела	1
Пояснить схему алгоритма Робертса	2
Пояснить схему алгоритма поворота объекта № 3 вокруг оси 0Z	2

 

9 Метод Z-буфера

 

Цель работы: изучение алгоритма удаления невидимых граней методом
Z-буфера.

Алгоритм, использующий Z-буфер, это один из простейших алгоритмов удаления невидимых поверхностей. Работает этот алгоритм в пространстве изображения. Идея Z-буфера является простым обобщением идеи о буфере кадра. Буфер кадра используется для запоминания атрибутов (интенсивности) каждого пиксела в пространстве изображения, Z-буфер – это отдельный буфер глубины, используемый для запоминания координаты z или глубины каждого видимого пиксела в пространстве изображения. В процессе работы глубина или значение z каждого нового пиксела, который нужно занести в буфер кадра, сравнивается с глубиной того пиксела, который уже занесен в Z-буфер. Если это сравнение показывает, что новый пиксел расположен впереди пиксела, находящегося в буфере кадра, то новый пиксел заносится в этот буфер и, кроме того, производится корректировка Z-буфера новым значением z. Если же сравнение дает противоположный результат, то никаких действий не производится. По сути, алгоритм является поиском по х и у наибольшего значения функции z(х, у).

Формальное описание алгоритма Z-буфера таково:

1) заполнить буфер кадра фоновым значением интенсивности или цвета;

2) заполнить Z-буфер минимальным значением z;

3) преобразовать каждый многоугольник в растровую форму в произвольном порядке;

4) для каждого Пиксел(x, y) в многоугольнике вычислить его глубину z(х, у);

5) сравнить глубину z(х, у) со значением Z-буфер(х, у), хранящимся в
Z-буфере в этой же позиции;

6) если z(х, у) > Z-буфер(х, у), то записать атрибут этого многоугольника (интенсивность, цвет и т. п.) в буфер кадра и заменить Z-буфер(х, у) на z(х, у). В противном случае никаких действий не производить.

Если известно уравнение плоскости, несущей каждый многоугольник, то вычисление глубины каждого пиксела на сканирующей строке можно проделать пошаговым способом. Грань при этом рисуется последовательно (строка за строкой). Для нахождения необходимых значений используется линейная интерполяция (рисунок 9.1).

 

 

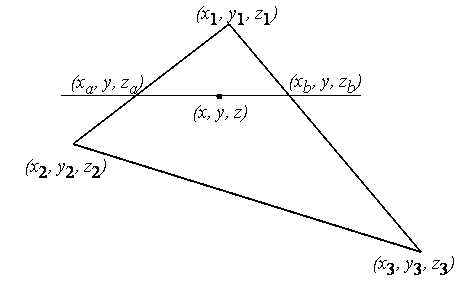
Рисунок 9.1 – Сканирующая строка по грани

 

Для рисунка y меняется от y₁ до y₂ и далее до y₃, при этом для каждой строки определяется x_a, z_a, x_b, z_b:

 

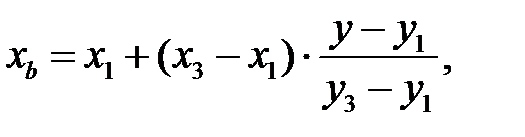
		(9.1)
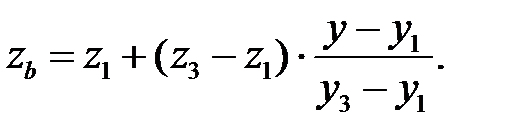
		(9.2)

 

На сканирующей строке x меняется от x_a до x_b и для каждой точки строки определяется глубина z:

 

                  (9.3)

 

Реализация алгоритма вдоль сканирующей строки позволяет совместить алгоритм Z-буфера с алгоритмами растровой развертки ребер и алгоритмами закраски грани.

 

Практическое задание

 

Составить алгоритм и программу для визуализации сцены пересечения объекта № 3 и куба.

Содержание отчета: блок-схема данной программы; краткие ответы на вопросы, приведенные в таблице 9.1; распечатка листа Excel с результатами.

 

Таблица 9 – Вопросы для защиты

 

Вопрос	Рейтинг
Какая информация содержится в массиве листа «Z-буфер»	1
Привести формулу для определения глубины z(x, у)	1
Какая информация содержится в массиве листа «кадр»	1
Пояснить схему алгоритма для визуализации сцены пересечения объекта № 3 и куба	2