ЗАДАЧА БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ

Итак, мы будем рассматривать задачу безусловной оптимизации

 

f(x)min,                                                                                        (1)

 

где f: RmR. Точка x* Rm называется решением задачи (1) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> (или точкой глобального безусловного минимума функции f), если

 

f(x*) f(x)                                                                                       (2)

 

при всех x Rm. Если неравенство (2) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> выполнено лишь для x, лежащих в некоторой окрестности Vx* точки x*, то точка x* называется локальным решением задачи (1) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html>, или точкой локального безусловного минимума функции f. Если неравенство (2) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> строгое при всех x x*, то говорят о строгом глобальном и, соответственно, строгом локальном минимумах. Решение задачи (1) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> иногда обозначают argmin f(x) (или, более полно, argmin Rm f(x); когда речь идет о задачах безусловной оптимизации в обозначениях argminx Rm f(x) и minx Rm f(x) мы будем всегда опускать индекс "x Rm"). Обычно из контекста ясно о каком минимуме (локальном, глобальном и т. д.) идет речь.

Аналогичные понятия (максимумов) определяются для задачи

(x) max.

 

. ГРАДИЕНТНЫЕ МЕТОДЫ

 

2.1 Общие соображения и определения

 

Градиентные методы оптимизации относятся к численным методам поискового типа. Они универсальны, хорошо приспособлены для работы с современными цифровыми вычислительными машинами и в большинстве случаев весьма эффективны при поиске экстремального значения нелинейных функций с ограничениями и без них, а также тогда, когда аналитический вид функции вообще неизвестен. Вследствие этого градиентные, или поисковые, методы широко применяются на практике.Сущность указанных методов заключается в определении значений независимых переменных, дающих наибольшие изменения целевой функции. Обычно для этого двигаются вдоль градиента, ортогонального к контурной поверхности в данной точке. Различные поисковые методы в основном отличаются один от другого способом определения направления движения к оптимуму, размером шага и продолжительностью поиска вдоль найденного направления, критериями окончания поиска, простотой алгоритмизации и применимостью для различных ЭВМ. Техника поиска экстремума основана на расчетах, которые позволяют определить направление наиболее быстрого изменения оптимизируемого критерия.

Наиболее распространенные и эффективные методы приближенного решения задачи безусловной оптимизации

 

f(x) min,                                                                                       (1)

 

где f: Rm R, укладываются в следующую грубую схему. Начиная с некоторого x0 Rm, строится последовательность {xn} Rm такая, что

 

f(xn+1) < f(xn)                                                                             (2)

при всех n N. Такие последовательности иногда называют релаксационными, а методы построения релаксационных последовательностей - итерационными методами или методами спуска. Последовательность, удовлетворяющую (<http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>), строят в надежде, что уменьшая на каждом шаге (переходе от xn к xn+1) значение функции, мы приближаемся к минимуму (по крайней мере, локальному).

Мы будем говорить, что метод, начиная с данного x0 Rm,

а) условно сходится, если последовательность {xn} релаксационна <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> и

(xn) при n;

 

б) сходится, если

 

xn x* = argmin f(x) при n;

 

в) линейно сходится (или сходится со скоростью геометрической прогрессии, или имеет первый порядок сходимости), если при некоторых C > 0 и q [0, 1)

 

||xn  x*|| Cqn;                                                                            (3)

 

г) сверхлинейно сходится, если для любого q (0, 1) и некоторого (зависящего от q) C выполнено неравенство (3) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>;

д) квадратично сходится (или имеет второй порядок сходимости), если при некоторых C > 0 и q [0, 1) и всех n  <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/1.html>

 

||xn  x*|| Cq2n.

 

Если эти свойства выполняются только для x0 достаточно близких к x*, то как всегда добавляется эпитет "локально".

2.2 Эвристические соображения, приводящие к градиентным методам

 

Выше уже отмечалось <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html>, что если x не является точкой локального минимума функции f, то двигаясь из x в направлении, противоположном градиенту (еще говорят, в направлении антиградиента), мы можем локально уменьшить значение функции. Этот факт позволяет надеяться, что последовательность {xn}, рекуррентно определяемая формулой

 

xn+1 = xn f (xn),                                                                       (4)

 

где - некоторое положительное число, будет релаксационной <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>.

К этой же формуле приводит и следующее рассуждение. Пусть у нас есть некоторое приближение xn. Заменим в шаре B(xn, ) с центром в точке xn функцию fее линейным (вернее, афинным) приближением:

 

f(x) (x) f(xn) + (f (xn), x  xn)

 

(функция аппроксимирует f в окрестности точки xn с точностью o(x - xn) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html>). Разумеется, (линейная) безусловная задача (x) min неразрешима, еслиf (xn) (см. задачу 1.3 <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/1.html>). В окрестности же B(xn,) функция имеет точку минимума. Эту точку естественно взять за следующее приближение xn+1.

 

2.3 Градиентный метод с постоянным шагом

 

В общем случае число в формуле (4) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> может на каждом шаге (т. е. для каждого n) выбираться заново:

 

xn+1 = xn nf (xn).                                                                     (5)

Именно методы, задаваемые формулой (<http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>), называются градентными. Если n = при всех n, то получающийся метод называется градиентным методом с постоянным шагом (с шагом.)

Поясним геометрическую суть градиентного метода. Для этого мы выберем способ изображения функции с помощью линий уровня. Линией уровня функции f(изолинией) называется любое множество вида {x Rm: f(x) = c}. Каждому значению c отвечает своя линия уровня (см. рис. <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>).

 

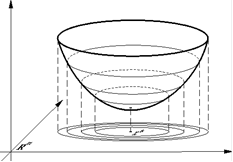
Рис.

 

Геометрическая интерпретация градиентного метода с постоянным шагом изображена на рис. <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> На каждом шаге мы сдвигаемся по вектору антиградиента, "уменьшенному в раз".

 

Рис.

 

2.4 Один пример исследования сходимости

 

Изучим сходимость градиентного метода с постоянным шагом <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> на примере функции

f(x) = |x|p,

 

где p > 1 (случай p 1 мы не рассматриваем, поскольку тогда функция f не будет гладкой, а мы такой случай не исследуем). Очевидно, задача (1) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> с такой функцией f имеет единственное решение x* = 0. Для этой функции приближения xn градиентного метода имеют вид:

 

xn+1 = xn |xn|p1sign xn.                                                       (6)

 

Пределом этой последовательности может быть только 0. Действительно, если x** = limn xn 0, то, переходя к пределу в (6) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> при n, получаем противоречащее предположению x** 0 равенство

 

x** = x** p|x**|p1sign x**

 

откуда x** = 0. Очевидно также, что если x0 = 0, то и xn = 0 при всех n.

Покажем, что если p < 2, то при любом шаге > 0 и любом начальном приближении x0 (за исключением не более чем счетного числа точек) приближения (6) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>не являются сходящимися. Для этого заметим, что если 0 < |xn| < (2/p)1/2(2p), то

 

|xn+1| > |xn|.                                                                                (7)

 

Поэтому, если xn не обращается в нуль, то она не может сходиться к нулю и, следовательно, не может сходиться вообще.

Таким образом, осталось доказать (7) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>. В силу (6) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>

 

|xn+1| = |xn p|xn|p1 ·sign xn| = |xn|·| 1 p|xn|p2·sign xn|.

 

Остается заметить, что если 0 < |xn| < (2/p)1/(2p), то, как нетрудно видеть, |1  |xn|p2·sign xn| > 1, что и требовалось.

Таким образом, есть функции, для которых градиентный метод не сходится даже при сколь угодно малом шаге и есть функции, для которых он сходится только при достаточно малых шагах. В следующих пунктах мы приведем ряд теорем о сходимости градиентного метода.

 

2.5 Теорема об условной сходимости градиентного метода с постоянным шагом

 

Пусть в задаче (1) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> функция f ограничена снизу, непрерывно дифференцируема и, более того, f удовлетворяет условию Липшица <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html>:

 

||f (x)  f (y)|| ||x  y|| при всех x, y Rm.

 

Тогда при (0, 2/) градиентный метод с постоянным шагом <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> условно сходится <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>.

Доказательство.

Положим zn = f (xn) и обозначим f(xn + tzn) через (t). Тогда, как легко видеть,

 

(t) = (f (xn + tzn), zn)

 

и поэтому по формуле Ньютона - Лейбница для функции

(xn+1)  f(xn) = f(xn + zn)  f(xn) = (1) (0) =1 0(s) ds = 1(f (xn+ szn), zn) ds.

 

Добавив и отняв (f (xn), zn) = 01(f (xn), zn) dsи воспользовавшись неравенством (x, y) ||x|| · ||y||, получим

 

f(xn+1)  f(xn) = (f (xn), zn) +1 0 (f (xn + szn) f (xn), zn) ds

(f (xn), f (xn)) + 1||f (xn + szn)  f(xn)|| · ||zn|| ds.

 

Учитывая условие Липшица для f , эту цепочку можно продолжить:

(xn+1)  f(xn) ||f (xn)||2 + ||zn||2 0s ds =||f (xn)||2 +2 2||f (xn)||2 = ||f (xn)||2

 

Поскольку 1 /2 > 0, последовательность {f(xn)} не возрастает и, следовательно, релаксационность <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> {xn} доказана. А так как в силу условий теоремы f еще и ограничена снизу, последовательность {f(xn)} сходится. Поэтому, в частности, f(xn+1)  f(xn) 0 при n. Отсюда и из (8) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> получаем

 

||f (xn)||2 1 1 - 2 -1 [f(xn)  f(xn+1)] 0 при n

 

2.6 Замечания о сходимости

 

Подчеркнем, что теорема 3.5 <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> не гарантирует сходимости <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> метода, но лишь его условную сходимость <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>, причем, локальную <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>. Например, для функции f(x) =(1 + x2)1 на R последовательность {xn} градиентного метода с постоянным шагом <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>, начинающаяся с произвольного x0 стремится к.

Поскольку в теореме 3.5 <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> градиент непрерывен, любая предельная точка последовательности {xn} является стационарной <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html>. Однако эта точка вовсе не обязана быть точкой минимума, даже локального. Например, рассмотрим для функции f(x) = x2sign x градиентный метод с шагом (0, 1/2). Тогда, как легко видеть, если x0 > 0, то xn 0 при n. Точка же x = 0 не является локальным минимумом функции f.

Заметим также, что описанный метод не различает точек локального <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> и глобального минимумов <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html>. Поэтому для того, чтобы сделать заключение о сходимости xnк точке x* = argmin f(x) приходится налагать дополнительные ограничения, гарантирующие, в частности, существование и единственность решения задачи (1) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>. Один вариант таких ограничений описывается ниже.

 

2.7 Теорема о линейной сходимости градиентного метода с постоянным шагом

 

Пусть выполнены условия теоремы 3.5 <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> и, кроме того, f дважды непрерывно дифференцируема и сильно выпукла с константой <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html>. Тогда при (0, 2/)градиентный метод с шагом  сходится со скоростью геометрической прогрессии <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> со знаменателем q = max{|1 |, |1  |}:

 

||xn  x*|| qn||x0  x*||.

 

Доказательство.

Решение x* = argmin f(x) существует и единственно в силу теорем 2.9 <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> и 2.10 <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html>. Для функции F(x) = f (x) воспользуемся аналогом формулы Ньютона - Лейбница

 

F(y) = F(x) + 1 0F [x + s(y  x)](y x) ds,

 

или, для x = x* и y = xn, учитывая, что f (x*) = <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/1.html>,

 

f (xn) = 1 0 f [x* + s(xn  x*)](xn  x*) ds

 

(здесь мы, как и выше, воспользовались задачей 2.3 <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html>). Далее, в силу утверждения (2.5) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> из п. 2.3 f (x) при всех x Rm. Кроме того по условию f (x) при тех же x. Поэтому, так как

 

||h||2 (f [x* + s(xn x*)]h, h) ||h||2

 

выполнено неравенство

||h||2 1 f [x* + s(xn x*)] ds h, h ||h||2

 

Интеграл, стоящий в этом неравенстве, определяет линейный (симметричный <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> в силу симметричности f) оператор на Rm, обозначим его Ln. Неравенство (10) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>означает, что Ln В силу (9) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> градиентный метод (4) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> записывается в виде

+1 = xn Ln(xn  x*)

 

Но тогда ||xn+1  xn|| = ||xn x* Ln(xn  x*)|| = ||(I Ln)(xn  x*)|| ||I Ln|| ||xn  x*||.

 

Спектр (I Ln) оператора I Ln состоит из чисел вида i = 1 i

 

где i (Ln). В силу (10) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> и неравенства (2.3) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html>

и следовательно ||I  Ln|| max{|1 |, |1 |} = q.

Таким образом, ||xn+1  xn|| q||xn  x*||.

 

2.8 Об оптимальном выборе шага

 

Константа q, фигурирующая в теореме 2.7 <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> и характеризующая скорость сходимости метода, зависит от шага . Нетрудно видеть, что величина

= q() = max{|1 |, |1 |}

 

минимальна, если шаг выбирается из условия |1 | = |1  | (см. рис. 7 <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>), т. е. если = * = 2/(+ ). При таком выборе шага оценка сходимости будет наилучшей и будет характеризоваться величиной q = q*

квадратичный градиентный линейный шаг

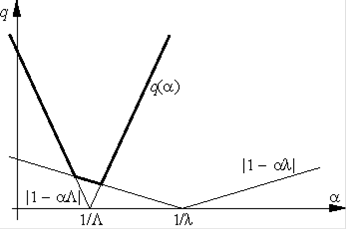
Рис.

 

Напомним, что в качестве и могут выступать равномерные по x оценки сверху и снизу собственных значений оператора f (x). Если <<, тоq* 1 и метод сходится очень медленно. Геометрически случай << соответствует функциям с сильно вытянутыми линиями уровня (см. рис. 8 <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>). Простейшим примером такой функции может служить функция на R2, задаваемая формулой

 

f(x1, x2) = x21+ x22с <<

 

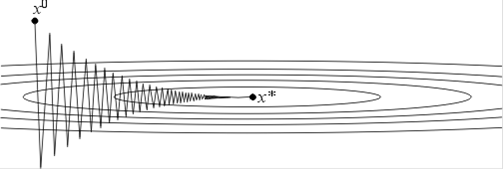
Рис.

 

Поведение итераций градиентного метода для этой функции изображено на рис. 8 <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> - они, быстро спустившись на "дно оврага", затем медленно "зигзагообразно" приближаются к точке минимума. Число = / (характеризующее, грубо говоря, разброс собственных значений оператора f (x)) называютчислом обусловленности функции f. Если >> 1, то функции называют плохо обусловленными или овражными. Для таких функций градиентный метод сходится медленно.

Но даже для хорошо обусловленных функций проблема выбора шага нетривиальна в силу отсутствия априорной информации о минимизируемой функции. Если шаг выбирается малым (чтобы гарантировать сходимость), то метод сходится медленно. Увеличение же шага (с целью ускорения сходимости) может привести к расходимости метода. Мы опишем сейчас два алгоритма автоматического выбора шага, позволяющие частично обойти указанные трудности.

 

2.9 Градиентный метод с дроблением шага

 

В этом варианте градиентного метода величина шага n на каждой итерации выбирается из условия выполнения неравенства

(xn+1) = f(xn nf (xn)) f(xn) n||f (xn)||2

 

где (0, 1) - некоторая заранее выбранная константа.

Условие (11) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> гарантирует (если, конечно, такие n удастся найти), что получающаяся последовательность будет релаксационной <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>. Процедуру нахождения такого n обычно оформляют так. Выбирается число (0, 1) и некоторый начальныйшаг 0. Теперь для каждого n полагают n = 0 и делают шаг градиентного метода. Если с таким n условие (11) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> выполняется, то переходят к следующему n. Если же (11) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> не выполняется, то умножают n на ("дробят шаг") и повторяют эту процедуру до тех пор пока неравенство (9) не будет выполняться. В условиях теоремы 3.5 <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> эта процедура для каждого n за конечное число шагов приводит к нужному n.

Можно показать, что в условиях теоремы 3.7 <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> градиентный метод с дроблением шага <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> линейно сходится <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>. Описанный алгоритм избавляет нас от проблемы выбора на каждом шаге, заменяя ее на проблему выбора параметров, и 0, к которым градиентный метод менее чувствителен.

При этом, разумеется, объем вычислений возрастает (в связи с необходимостью процедуры дробления шага), впрочем, не очень сильно, поскольку в большинстве задач основные вычислительные затраты ложатся на вычисление градиента.

 

Метод наискорейшего спуска

 

Этот вариант градиентного метода основывается на выборе шага из следующего соображения. Из точки xn будем двигаться в направлении антиградиента <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> до тех пор пока не достигнем минимума функции f на этом направлении, т. е. на луче L = {x Rm: x = xn f (xn); 0}:

 

n = argmin [0,)f(xn f (xn))

 

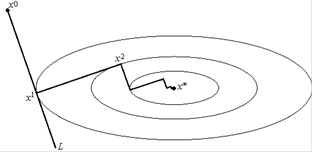
Рис.

 

Другими словами, n выбирается так, чтобы следующая итерация была точкой минимума функции f на луче L. Такой вариант градиентного метода называется методом наискорейшего спуска. Заметим, кстати, что в этом методе направления соседних шагов ортогональны. В самом деле, поскольку функция: f(xn f (xn)) достигает минимума при = n, точка n является стационарной точкой <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> функции:

 

0 = (n) =d d f(xn f (xn)) = n = (f (xn nf (xn)), f (xn)) = (f (xn+1), f (xn)).

 

Метод наискорейшего спуска <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> требует решения на каждом шаге задачи одномерной оптимизации (12 <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>). Такие задачи будут обсуждаться ниже <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/5.html>. Практика показывает, что этот метод часто требует меньшего числа операций, чем градиентный метод с постоянным шагом <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>.

В общей ситуации, тем не менее, теоретическая скорость сходимости метода наискорейшего спуска не выше скорости сходимости градиентного метода с постоянным (оптимальным) шагом.

 

 

3. МЕТОД НЬЮТОНА

 

3.1 Эвристические соображения, приводящие к методу Ньютона безусловной оптимизации

 

Если исходить из того, что необходимым этапом нахождения решения задачи

(x) min

 

где f: Rm R, является этап нахождения стационарных точек <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html>, т. е.точек, удовлетворяющих уравнению

 

F(x) f (x) = <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/1.html>

 

(обозначение F для f  мы будем сохранять на протяжении всего параграфа), то можно попытаться решать уравнение (2) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> известным методом Ньютона решения нелинейных уравнений

 

xn+1 = xn  [F (xn)]1F(xn)

 

Для задачи (1) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> этот метод называется методом Ньютона безусловной оптимизации и задается формулой

+1 = xn  [f (xn)]1f (xn)

 

Формула (3) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> может быть выведена, исходя из следующих соображений. Пусть xn - некоторое приближенное решение уравнения (2) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>. Тогда если заменить функцию F в уравнении (2) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> ее линейным приближением(x) (x) F(xn) + F (xn)(x  xn)

 

и взять в качестве следующего приближения решение уравнения то мы получим формулу (3) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>.

Применительно к задаче (1) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> эти соображения выглядят так. Пусть так же, как и в п. 3.2 <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> у нас уже есть некоторое приближенное решение xn задачи (1) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>. Заменим в ней функцию f ее приближением второго порядка:

 

f(x) (x) f(xn) + (f (xn), x  xn) +1 2    (f (xn)(x  xn), x  xn)

 

и в качестве следующего приближения возьмем решение задачи

 

(x) min

 

Геометрическая интерпретация формул (3) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> и (4) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> приведена на рис. 10а и 10б. <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>

 

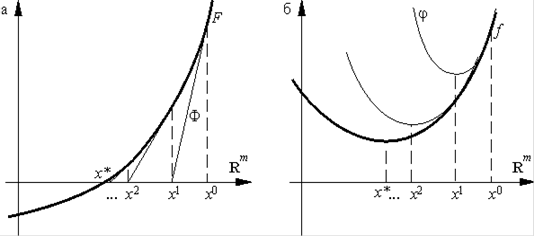
Рис.

 

Метод Ньютона относится к методам второго порядка, поскольку для вычисления каждой итерации требуется знание второй производной функции f. По тем же соображениям градиентный метод относят к методам первого порядка. Подчеркнем, что здесь речь идет не о порядке сходимости метода, а о порядке используемых методом производных минимизируемой функции.

 

3.2. Теорема о локальной сверхлинейной сходимости метода Ньютона

 

Пусть f дважды непрерывно дифференцируема, а x* - невырожденная стационарная точка <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html>. Тогда найдется окрестность Vx* точки x* такая, что приближения (4) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>, начатые из произвольной начальной точки x0  Vx*, сверхлинейно сходятся <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> к x*.

Доказательство.

Очевидно, F = f C1 и поэтому

x x* ||F (x)  F (x*)|| = 0.

 

Поскольку F (x*) невырожден, в силу (7) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> при x достаточно близких к x* невырожден и оператор F (x) и более того,

x x* ||[F (x)]1  [F (x*)]1|| = 0.

 

Поэтому, в частности, при x достаточно близких к x*

 

||[F (x)]1|| C

 

Далее, в силу того, что F дифференцируема, а x* - стационарная точка,

 

F(x) = F(x*) + F (x*)(x  x*) + o(x - x*) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> = F (x*)(x  x*) + o(x - x*) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html>,

 

Но тогда в силу

 

x x* [F (x)]1F(x) = [F (x)]1F (x)(x  x*)  [F (x)]1F(x) = [F (x)]1[F (x)(x  x*) F(x)] = o(x  x*).

или

x  [F (x)]1F(x)  x* = o(x  x*).

 

В частности, при x = xn

 

xn+1 x* = xn [F (xn)]1F(xn) x* (xn x*) = o(xn x*)

 

Возьмем теперь в качестве Vx*, например, окрестность {x Rm: ||(x  x*)|| ||x  x*||/2}. В силу (9) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>, очевидно, если x0 Vx*, то

 

||xn+1  x*|| 1

||xn  x*|| ... 1

2n+1 ||x0  x*||

 

и, следовательно, xn x* при n. Более того, для произвольного q (0, 1) найдется > 0 такое, что ||(x  x*)|| q||x  x*|| при ||x  x*||. Но тогда, если||xn  x*||, то ||xn+1  x*|| q||xn  x*||. Из последнего утверждения очевидным образом вытекает нужное соотношение ||xn  x*|| Cqn.

 

3.3 Обсуждение метода Ньютона

 

Таким образом, метод Ньютона <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>, с одной стороны, может сходиться с более высоким чем градиентный метод <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> порядком <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>, а, с другой стороны, для его сходимости требуются достаточно хорошие начальные приближения (по крайней мере так требуется в доказанной теореме).

Простой геометрический пример (см. рис. <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>) подтверждает эту особенность метода (мы приводим пример для уравнения (2) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>; соответствующий пример для задачи (1) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> получается "интегрированием").

 

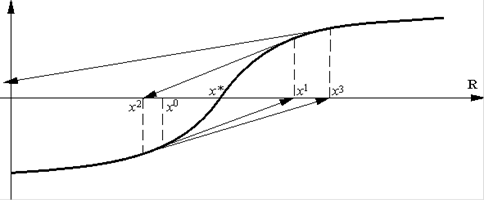
Рис.

 

Разумеется, как метод второго порядка <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>, метод Ньютона требует большего объема вычислительной работы, поскольку приходится вычислять вторые производные функции f.

К этому сводятся основные преимущества (высокий порядок сходимости) и недостатки (локальный характер сходимости и больший объем вычислений) метода Ньютона.

Если функция f дополнительно сильно выпукла, то можно утверждать сходимость именно к решению <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> задачи (1) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>, а не только к стационарной точке <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> функции f, и, кроме того, оценить радиус окрестности, из которой приближения Ньютона сходятся.

 

3.4 Теорема о квадратичной сходимости метода Ньютона

 

Пусть f C2 и, более того, f удовлетворяет условию Липшица <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> с константой L. Пусть f сильно выпукла с константой <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html>. Пусть Vx* - окрестность решения задачи (1) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>, состоящая из точек x Rm таких, что

||f (x)|| <2 2 L

 

Тогда для x0 Vx* метод Ньютона <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> квадратично сходится <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>:

 

||xn  x*|| 2

L q2n,

 

где q = L||f (x0)||/2 2 < 1.

Доказательство.

По теореме 2.9 <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> и 2.10 <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> в условиях нашей теоремы решение x* задачи (1) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> существует и единственно. Воспользуемся аналогом формулыНьютона - Лейбница для функции f:

(xn + h)  f (xn) = 1 0f (xn + sh)h ds

 

Вычитая из обеих частей этого равенства f(xn)h = 01f (xn)h dsи учитывая, что f удовлетворяет условию Липшица <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html>, получаем (ср. <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>).

 

||f (xn + h) f (xn)  f (xn)h|| 1 0 [f (xn + sh) f (xn)]h ds

1 0 ||f (xn + sh)  f (xn)|| · || h|| ds 1 0||h||2ds =L

||h||2.

 

Положим в полученной оценке h = [f (xn)]1f (xn):

 

||f (xn + h) f (xn) + f (xn)[f (xn)]1f (xn)|| = || f (xn+1)|| L

||[f (xn)]1f (xn)||2 L

||[f (xn)]1||2·||f (xn)||2.

 

Поскольку f сильно выпукла, f (xn) и поэтому (см. пред. задачу <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>) ||[f (xn)]1|| 1. Продолжая неравенство (10) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>, получаем

 

||f (xn+1)|| L

||f (xn)||2.

 

С помощью (11) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> индукцией по n легко доказывается неравенство

 

||f (xn)|| L

2 2n1||f (x0)||2n =2

||f (x0)||

n =2 2

L q2n.

 

Наконец, в силу сильной выпуклости <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> f, так как x* - решение задачи (1) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> и, следовательно, f (x*) = <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/1.html>,

 

f(x*)  f(xn) (f (xn), x*  xn) + ||xn  x*|| 2,

или

(f (xn), xn  x*) || xn  x*|| 2.

Но тогда

||xn x*|| 2 (f (x*), xn  x*) ||f (x*)|| · ||xn  x*||,

откуда ||f (x*)|| || xn  x*||

 

Тогда из (12) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> следует нужное неравенство.

 

Продолжение обсуждения метода Ньютона

 

Из доказанной теоремы <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> следует, что чем меньше константа Липшица <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> отображения x f (x), т. е. чем ближе это отображение к константе, и, следовательно, чем ближе функция f к квадратичной, тем быстрее сходится метод Ньютона <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>. В частности, если f квадратична: f(x) = (Ax, x)/2 + (b, x) + c, то метод Ньютона конечен, а именно, сходится за один шаг, причем из любой начальной точки.

Если снизить требования гладкости на функцию f, например, отказаться от условия Липшица <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> для f, то скорость сходимости, вообще говоря, падает.

Как позволяет думать теорема 4.4 <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>, метод Ньютона даже для сильно выпуклых <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> функций в общем случае сходится лишь локально <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>. В следующем пункте мы описываем модификации этого метода, которые могут обладать свойством глобальной сходимости.

 

3.6 Методы Ньютона с регулировкой шага

 

Эти методы еще называют методами Ньютона - Рафсона, или демпфированными методами Ньютона. Они строятся по аналогии с градиентными методами с переменным шагом <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>. Общий вид их таков

+1 = xn n[f (xn)]1f (xn)

 

Длина шага может выбираться с помощью алгоритма дробления шага (см. п. 2.9 <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>), требуя, например, выполнения неравенства

(xn+1) = f(xn n[f xn)]1f (xn)) f(xn) n(f (xn), [f (xn)]1f (xn))

 

или, как в методе наискорейшего спуска <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> полагая

 

n = argmin0{f(xn [f (xn)]1f (xn))}

 

Можно показать, что -методы Ньютона Рафсона <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> для сильно выпуклых <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> функций глобально <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> квадратично сходятся <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> (по крайней мере для описанных выше алгоритмов выбора шага), причем вдали от точки минимума они сходятся линейно <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>.

 

3.7 Метод Левенберга - Маркардта

 

Этот метод основан на следующей идее. Чтобы избежать расходимости приближений метода Ньютона <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>, вызванных неудачным выбором начального приближения (см. рис. 11 <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>), можно попытаться запретить следующей итерации быть слишком далеко от предыдущей. Для этого следующую итерацию ищут из условия

+1 = argmin (x) argmin {f(xn) + (f (xn), x  xn) +1

(f (xn)(x  xn), x  xn) +ln

||x  xn||2}

 

где ln - некоторый параметр (вообще говоря, свой на каждом шаге). Первые три слагаемых в определении функции  представляют собой квадратичную аппроксимацию функции f, а последнее слагаемое - "штраф", не позволяющий точке xn+1 уходить далеко от точки xn (с идеями метода штрафов мы еще столкнемся ниже). Минимум <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> (по крайней мере, стационарная точка <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html>) функции  вычисляется в явном виде из следующего уравнения (относительно x)

 

<http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/1.html> = (x) = f (xn) + f (xn)(x xn) + ln(x xn).

 

Как легко видеть,

+1 = argmin (x) = xn  [f (xn) + lnI]1f (xn)

 

Последняя формула и есть метод Левенберга - Маркардта.

Очевидно, что если ln = 0, то (13) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> представляет собой метод Ньютона <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>, а если ln велико, то (поскольку [f (xn) + lnI]1 (ln)1I при больших ln) формула (13) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>близка к градиентному методу <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>. Поэтому, подбирая значения параметра ln, можно добиться, чтобы метод (13) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>, во-первых, сходился глобально <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>, и во-вторых,квадратично <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html>. Можно, например, выбирать ln из следующих соображений: угол между направлениями шага и антиградиента <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> должен быть острым, а значение функции на каждом шаге должно квалифицировано убывать. В этом случае ln должно удовлетворять следующим условиям (здесь мы обозначаем "антинаправление" шага [f (xn) + lnI]1f (xn) через yn)

 

(yn, f (xn))

||yn|| · || f (xn)||1

f(xn+1) f(xn) 2(yn, f (xn))

 

где 1 (0, 1) и 2 (0, 1/2) - параметры.

 

3.8 Еще один недостаток метода Ньютона. Модифицированный метод Ньютона

 

В некоторых задачах более существенным недостатком метода Ньютона является его большая вычислительная трудность: на каждом шаге требуется вычисление оператора (матрицы) f (xn) и его (ее) обращение, что при больших размерностях стóит в вычислительном плане очень дорого. Один из способов обхода этих трудностей состоит в "замораживании" оператора f (xn) - использовании на каждом шаге [f (x0)]1 взамен [f (xn)]1:

+1 = xn  [f (x0)]1f (xn)

Геометрическая интерпретация модифицированного метода Ньютона (14) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> изображена на рис. <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>

 

Рис.

 

Можно показать, что при естественных ограничениях модифицированный метод Ньютона сходится лишь линейно (это плата за уменьшение объема вычислений). Можно также не замораживать оператор [f (xn)]1 навсегда, а обновлять его через определенное число шагов, скажем k:

+1 = xn  [f (x[n/k]·k)]1f (xn)

 

здесь [a] в верхнем индексе обозначает целую часть числа a. Можно доказать, что если функция f сильно выпукла <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> и f удовлетворяет условию Липшица <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html>, то

 

||xn+k  x*|| C||xn  x*||k+1,

 

т. е. за k шагов порядок погрешности уменьшается в k + 1 раз, что соответствует следующей оценке погрешности на каждом шаге:

 

||xn+1  x*|| C||xn  x*||k k+1.

 

Другими словами, метод (15) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> является методом kk+1-го порядка сходимости. Таким образом, метод (15) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> занимает промежуточное положение между методом Ньютона <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> (k = 1) и модифицированным методом Ньютона <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> (14) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> (k =) как по скорости сходимости, так и по объему вычислений.

Другой способ уменьшения объема работы, связанного с вычислением функции f (xn) описывается в следующем пункте.

 

3.9 Метод секущих

 

Напомним, что метод секущих решения уравнения (2) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> заключается в приближенной замене функции F в этом уравнении не касательной y = F(xn) +F (xn)(x  xn), а секущей гиперплоскостью.

Например, в одномерном случае - прямой y = F(xn) + (F(xn)  F(xn1))(x xn) /(xn xn1). Эта замена приводит (в скалярном случае!) к следующему методу решения задачи (1) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>:

+1 = xn  xn  xn1

f (xn) f (xn1)(xn)

 

который и называется методом секущих.

Известно, что для достаточно гладких выпуклых функций <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/2.html> порядок сходимости <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> этого метода равен, где = (5 + 1)/2 1.618 - известная константа (называемая золотым сечением).

 

 

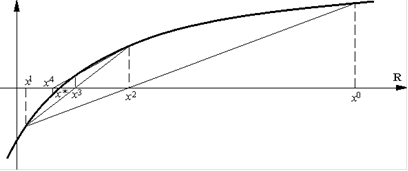
Рис.

 

В многомерном случае поступают следующим образом. Пусть xn, xn1, ..., xnm - уже вычисленные m + 1 итерации.

Для каждой компоненты fj функции f (j = 1, ..., m) построим в Rm+1 гиперплоскость Sj, проходящую через m + 1 точку (xi, fj(xi)) (i = n  m, ..., n) графика этой компоненты. Пусть P -"горизонтальная" проходящая через нуль гиперплоскость в Rm+1: P = {(x, y) Rm×R; y = 0}. В качестве xn+1 возьмем точку пересечения гиперплоскостей P иSj:

+1 P mj = 1 Sj

 

(в общем положении эта точка единственна).

Несложные рассуждения показывают, что xn+1 можно вычислять так. Пусть 0, ..., n - решение системы

i = 0 if (xni) = 0, m i = 0 i = 1.

Тогда

xn+1 = m i = 0 ixni

 

Затем описанные действия повторяются для точек xn+1, xn, ..., xnm+1.

Отметим, что поскольку на каждом шаге в системе (16) <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> меняется лишь один столбец, то ее решение на каждом шаге можно обновлять с помощью специальной процедуры, не требующей большого объема вычислений.

Отметим, что метод секущих <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html>, в отличие от ранее рассматривавшихся методов, не является одношаговым в том смысле, что для вычисления следующей итерации ему не достаточно информации, полученной на предыдущем шаге - нужна информация, полученная на m + 1 предыдущих шагах. Такие методы называются многошаговыми. В следующем параграфе мы рассмотрим ряд таких методов. Методы же Ньютона <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/4.html> и градиентный <http://www.ict.nsc.ru/ru/textbooks/akhmerov/mo/3.html> являются одношаговыми: для вычисления xn+1 требуется знать поведение функции и ее производных только в точке xn.

 

 

ЗАКЛЮЧЕНИЕ

 

Алгоритмы безусловной минимизации функций многих переменных можно сравнивать и исследовать как с теоретической, так и с экспериме<