 |
Главная |
Л. И. Мандельштамом и Н. Д. Папалекси.
|
из
5.00
|
Рассмотрим систему стандартного вида
 (s=1,2) (1)
(s=1,2) (1)
Уравнение Ван-дер-Поля также можно привести к системе стандартного вида:
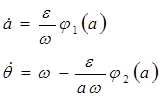 (2)
(2)
Сделаем замену
 ,
,
тогда:  (3)
(3)
Будем считать  =
=  .
.
Среднее значение функции  за период 2
за период 2  :
:

При этом усреднении интегрирование ведется по третьей переменной t в предположении, что 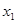 и
и  от t не зависят.
от t не зависят.

Наряду с точной системой рассматривается приближенная
 , (s=1,2).
, (s=1,2).
Обе системы, приближенная и точная, решаются при начальных условиях
 (4)
(4)
Для задач Коши (1) и (4), (3) и (4) справедлива следующая теорема:
Теорема. Пусть при всех t и в некоторой области переменных  функции
функции  непрерывны и ограничены. Функции
непрерывны и ограничены. Функции  также непрерывны и ограничены в области Г.
также непрерывны и ограничены в области Г.  — 2
— 2  -периодические по t. Функции
-периодические по t. Функции  и
и  — удовлетворяют условию Липшица по переменным
— удовлетворяют условию Липшица по переменным 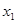 и
и  (при этих условиях существует и единственно решение). Тогда для
(при этих условиях существует и единственно решение). Тогда для 
 и L>0:
и L>0:
 (5)
(5)
0  (6)
(6)
Доказательство:
Решение задач Коши (1) и (4), (3) и (4) существует и единственно. Поэтому решение (1) и (4) будем искать методом приближений.

Обозначим
 (*)
(*)
Функция 
 — 2
— 2  -периодическая по
-периодическая по  .
.
Пусть
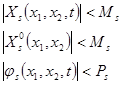 (7)
(7)
 удовлетворяет условиям Липшица по переменным
удовлетворяет условиям Липшица по переменным  и
и  . Проинтегрируем функцию
. Проинтегрируем функцию  :
:
 .
.
Интеграл  и
и  поэтому
поэтому

 (7a)
(7a)
В промежутке 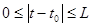 находятся те значения t, для которых будет существовать решение (1) - (4) и оно не выйдет за пределы области G. Это характеризуется так
находятся те значения t, для которых будет существовать решение (1) - (4) и оно не выйдет за пределы области G. Это характеризуется так

Из теоремы Пикара следует, что при всех таких t приближенное выражение сходится к решению задачи Коши:



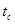 — целую часть от деления обозначим N. Тогда
— целую часть от деления обозначим N. Тогда  — дробная часть
— дробная часть 
 ,
,
где  — остаточный интервал.
— остаточный интервал.
С учетом возможности такого разбиения

Если рассмотреть  , то последнее выражение перепишется в виде:
, то последнее выражение перепишется в виде:
 =
=  ,
,
где с учетом (4)
 =
= 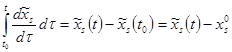
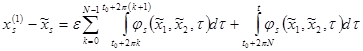
Рассмотрим интеграл при 
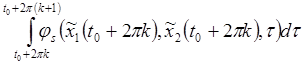
 и
и 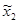 от
от 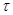 не зависят. Из равенств (7а) следует, что последнее выражение равно нулю
не зависят. Из равенств (7а) следует, что последнее выражение равно нулю  .
.
Вычислим

То есть

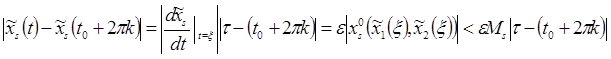

 (8)
(8)
Мы можем сказать, что в (8), все, что стоит под знаком суммы
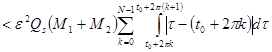
Так как
 ,
,
то последнее неравенство равносильно следующему:





 Поэтому:
Поэтому:

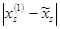 =
=  , (9)
, (9)
 где
где 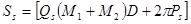

 (10)
(10)



 — удовлетворяет условию Липшица, поэтому мы можем воспользоваться этим, переходя к оценкам
— удовлетворяет условию Липшица, поэтому мы можем воспользоваться этим, переходя к оценкам

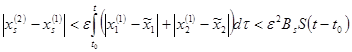 (11)
(11)



 (12)
(12)
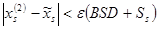
Пусть  , причем
, причем  , тогда:
, тогда:
 (13)
(13)
Оценим
 (14)
(14)
Фактически нужно оценить величину  .
.
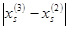
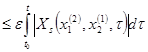
Используем условие Липшица для  , тогда последнее неравенство
, тогда последнее неравенство

(последняя оценка получена с помощью неравенства (11)).
 (15)
(15)
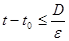
 (16)
(16)
Можно увидеть следующую закономерность
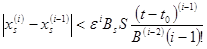 (17)
(17)
По методу математической индукции, для 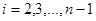 оценки верны. Покажем их справедливость и для
оценки верны. Покажем их справедливость и для 

Используя формулу (13), далее получим:
 (18)
(18)
Теперь в этом неравенстве перейдем к пределу при 
 (19)
(19)
Обозначим через
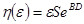
Так как мы пользовались условиями Липшица, нужно убедиться, что приближения не выходят из области G.
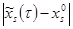 — по теореме Пикара это не выходит за пределы области G, то есть
— по теореме Пикара это не выходит за пределы области G, то есть

В силу плотности числовой прямой
 , где
, где  (20)
(20)
Проверим, вышло ли первое приближение за пределы области G. Пользуясь оценками (19) и (20), имеем:

Возьмем
 ,
,
тогда

Аналогично проверяем второе приближение
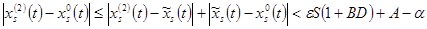
Возьмем
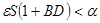 , тогда
, тогда


И если
 ,
,
если

Если мы перейдем к перейдем к пределу при  , то получим:
, то получим:
 (21)
(21)
Если мы  будем выбирать из условия (21), то использование условия Липшица законно.
будем выбирать из условия (21), то использование условия Липшица законно.
 необходимо согласовывать с
необходимо согласовывать с  с помощью (21) и
с помощью (21) и

Решение уравнения
Рассмотрим уравнение
 (1)
(1)
Данное уравнение второго порядка описывает колебательное движение. Здесь ω – некоторая действительная постоянная, а ε – малый параметр.
Делаем в уравнении (1) замену:  тогда получим систему
тогда получим систему
 (2)
(2)
Переходим в уравнении (1) к новым переменным a и  , полагая здесь и далее
, полагая здесь и далее 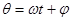 , согласно формулам
, согласно формулам
 (3)
(3)
Далее, дифференцируем (3) по t, считая 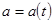 и φ
и φ 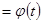 .
.
 (4)
(4)
Подставим (4) в (2), учитывая (3).

 (5)
(5)
Разрешим эту систему относительно 

Домножим второе уравнение на 

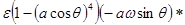
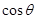 ,
,
тогда имеем:
 (6)
(6)
Система (6) полностью эквивалентна уравнению (1). Соответствующая системе (6) усредненная система имеет вид
 (7)
(7)
В системе (7)  и
и  имеют вид:
имеют вид:

то есть


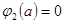
Таким образом имеем
 или
или

 (8)
(8)
Чтобы найти в явном виде закон изменения амплитуды в зависимости от времени, необходимо решить первое уравнение системы (8):

Умножим обе части равенства на  :
:
 .
.
Сделаем замену


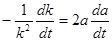
 ,
,
умножаем обе части равенства на  :
:



Так как  ,
,
то тогда 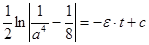 ,
,
или 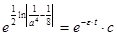



Предположим, что  , тогда
, тогда 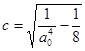
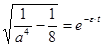
 ;
;  ;
;

 +
+  .
.
Отсюда находим
 (9а)
(9а)
Колебания представятся следующим образом (находим выражение для приближенного значения x в явном виде)
 (9)
(9)
Найдем 
Динамический режим обладает сильной устойчивостью, заключающейся в том, что каково бы ни было значение  , малое или большое, все равно
, малое или большое, все равно  при
при  .
.
Как видно из выражения (9), если начальное значение амплитуды  =0, амплитуда останется равной нулю для любого t, и, следовательно, получим х=0, то есть тривиальное решение уравнения (1). Это тривиальное решение, очевидно, соответствует статическому режиму, то есть отсутствию колебаний в системе.
=0, амплитуда останется равной нулю для любого t, и, следовательно, получим х=0, то есть тривиальное решение уравнения (1). Это тривиальное решение, очевидно, соответствует статическому режиму, то есть отсутствию колебаний в системе.
Однако, исходя из формулы (9), нетрудно заключить, что этот статический режим неустойчив. Действительно, как бы ни было мало начальное значение амплитуды, оно все равно будет монотонно приближаться к значениям, равным  . Таким образом, поскольку случайные малые толчки практически неизбежны, в рассматриваемой колебательной системе, находящейся в состоянии покоя, автоматически возбуждаются колебания с амплитудой, то есть система самовозбуждается.
. Таким образом, поскольку случайные малые толчки практически неизбежны, в рассматриваемой колебательной системе, находящейся в состоянии покоя, автоматически возбуждаются колебания с амплитудой, то есть система самовозбуждается.
Из выражения (9) следует, что если 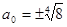 , то
, то  , и для любых
, и для любых 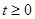
 очень быстро приближается к значению
очень быстро приближается к значению  независимо от
независимо от 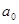 . Это решение соответствует стационарному (установившемуся) динамическому режиму:
. Это решение соответствует стационарному (установившемуся) динамическому режиму:
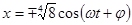 (10)
(10)
Иначе говоря, любое колебание при увеличении t приближается к стационарному колебанию, то есть колебания будут устойчивы.
Режимы с постоянной амплитудой, для  , приводят к уравнению
, приводят к уравнению
А  =
=  =0
=0
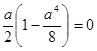 .
.
Корни этого уравнения 
 ;
;
 ;
;  <0
<0 


Таким образом,  соответствует неустойчивому состоянию равновесия, а
соответствует неустойчивому состоянию равновесия, а  соответствует устойчивому предельному циклу.
соответствует устойчивому предельному циклу.
Для любого заданного положительного сколь угодно малого значения параметра  всегда можно найти такое достаточно малое значение параметра
всегда можно найти такое достаточно малое значение параметра  , для которого уравнение (1) или, что то же самое, система (2), имела бы предельный цикл, лежащий в
, для которого уравнение (1) или, что то же самое, система (2), имела бы предельный цикл, лежащий в  окрестности окружности
окрестности окружности  , причем этот предельный цикл устойчив, если
, причем этот предельный цикл устойчив, если  , и неустойчив, если
, и неустойчив, если  . Все эти рассуждения следуют из теоремы Мандельштама и Папалекси.
. Все эти рассуждения следуют из теоремы Мандельштама и Папалекси.
Наряду с точной системой рассматривается приближенная
 , (s=1,2) .
, (s=1,2) .
Теорема. Пусть при всех t и в некоторой области переменных  функции
функции  непрерывны и ограничены. Функции
непрерывны и ограничены. Функции  также непрерывны и ограничены в области Г.
также непрерывны и ограничены в области Г.  — 2
— 2 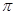 -периодические по t. Функции
-периодические по t. Функции  и
и  — удовлетворяют условию Липшица по переменным
— удовлетворяют условию Липшица по переменным  и
и  (при этих условиях существует и единственно решение). Тогда для
(при этих условиях существует и единственно решение). Тогда для 
 и L>0 :
и L>0 :  , 0
, 0 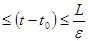 ,
,
где  (s=1,2)
(s=1,2)  =
= 

 (s=1,2)
(s=1,2)
Проверим выполнение условий теоремы для нашего уравнения. Из системы (6) находим 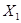 и
и  :
:

Очевидно, что  и
и  непрерывны.
непрерывны.
 , из этих неравенств видно, что
, из этих неравенств видно, что  и
и  ограничены для любого конечного
ограничены для любого конечного  . Функции
. Функции  и
и  для системы (2) имеют вид:
для системы (2) имеют вид:
 .
.
Из последней системы видно, что  и
и 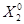 непрерывны и ограничены для любого конечного
непрерывны и ограничены для любого конечного  .
. 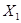 и
и  — периодические по t с любым периодом, в том числе и
— периодические по t с любым периодом, в том числе и  . Функции
. Функции 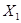 и
и 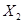 ,
,  и
и 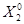 непрерывно дифференцируемы по t, а следовательно удовлетворяют условию Липшица.
непрерывно дифференцируемы по t, а следовательно удовлетворяют условию Липшица.
Пусть  и
и  — решения точной системы (6). Тогда для
— решения точной системы (6). Тогда для 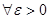
 и
и  :
:  ,
,  .
.
( В нашем случае  ,
,  определяется уравнением (9а)).
определяется уравнением (9а)).
Выводы
В рамках теории Ван-дер-Поля нельзя уточнить полученные решения.
В заключение заметим, что метод Ван-дер-Поля позволил исследовать достаточно широкий круг задач нелинейной механики (с одной степенью свободы), и задач радио- и электротехники, обладает наглядностью и удобен для проведения расчетов. Благодаря этому методу созданы генераторы стационарных колебаний в радиоприемных и радиопередающих устройствах, которые используются и по сей день в современной технике. В рамках теории Ван-дер-Поля нельзя уточнить полученные решения.
Список использованной литературы
1. Ю.А. Митропольский Метод усреднения в нелинейной механике, «Наукова думка» Киев — 1971г.
2. Н.Н. Моисеев Асимптотические методы нелинейной механики, М.: Наука, 1981г.
3. А. Найфэ Методы возмущений. Издательство «Мир», Москва—1976г.
4. А. Найфэ Введение в методы возмущений. «Мир», 1984г.
5. Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. Физматгиз, М.,1959г.
|
из
5.00
|
Обсуждение в статье: Л. И. Мандельштамом и Н. Д. Папалекси. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

