Метод прогонки решения систем с трехдиагональными матрицами коэффициентов

Введение

 

Три четверти прикладных математических задач в конечном итоге сводятся к решению систем алгебраических и трансцендентных уравнений, причем подавляющее большинство из них - линейные алгебраические системы, имеющие единственное решение.

Современная вычислительная математика обладает большим арсеналом методов, а математическое обеспечение ЭВМ - многими пакетами прикладных программ, позволяющих решать различные линейные системы. Казалось бы, этого достаточно, но на практике при решении линейных систем возникает множество разных проблем.

Поэтому ввиду большой важности и практической значимости задача решения линейных систем до сих пор привлекает внимание математиков. Создано большое количество разных методов решения этой задачи и сопутствующих ей задач (вычисление определителей, обратных матриц). Среди этих методов можно выделить две большие группы: прямые (или точные) и итерационные методы [4].

Прямые методы приводят к точному решению системы (если не учитывать вычислительные погрешности округлений), причем за конечное число шагов. К ним относятся методы Гаусса, LU-разложение, квадратного корня, методы прогонки, вращений и т.п. [2,4].

Итерационные методы позволяют получить приближенное решение системы с заданной точностью, используя идею последовательных приближений. К ним относятся методы простой итерации, Зейделя, релаксации, установления, спуска и т. п.[2,4].

Каждый из существующих методов решения линейных систем имеет свою сферу применения, где он является наиболее эффективным. Эффективность же названных численных методов зависит в основном от свойств матрицы системы (порядка, симметричности, меры обусловленности, заполненности).

Целью данной курсовой работы является:

обзор литературы по прямым методам решения линейных систем;

реализация метода квадратного корня средствами системы программирования Turbo Pascal.

Курсовая работа содержит две главы. Первая глава посвящена таким прямым методам решения линейных систем, как метод Гаусса, LU-разложение, метод прогонки для решения линейных систем с трехдиагональными матрицами коэффициентов и метод вращений для решения линейных систем. Во второй главе отдельно рассматривается метод квадратного корня для решения линейных систем, а именно: приведены теоретические основы метода, а также произведена его реализация в системе программирования Turbo Pascal.

Глава 1. Прямые методы решения линейных систем

Постановка задачи

 

К решению систем линейных уравнений сводятся многочисленные практические задачи. В данной курсовой работе изучается вопрос о численном решении систем вида [4]:

 

 (1.1.1)

 

Совокупность коэффициентов (aij), неизвестных (хi) и свободных членов (bi) этой системы запишем в виде матриц [4]:

= , x= , b= (1.1.2)

 

Помимо введенной матрицы А мы введем еще и расширенную матрицу системы, получающуюся из матрицы А добавлением столбца правых частей:

 

 (1.1.3)

Матрица системы А и столбец правых частей b считаются заданными, а столбец x ищется, при этом определитель матрицы не должен равняться 0.

 

Метод Гаусса

Данный метод является наиболее простым и популярным способом решения линейных систем вида (1.1.1). Он основан на последовательном исключении неизвестных [5].

Итак, пусть дана система (1.1.1). Для удобства можно представить её в виде (1.1.3). На первом этапе разделим все коэффициенты первой строки, а также свободный член на первый коэффициент. Таким образом перед х1 в первой строке получится единица. Теперь наша задача - исключить переменную х1 из остальных строк, другими словами сделать коэффициенты перед х1 нулевыми. Для этого заменяем все уравнения, начиная со второго, уравнениями, полученными сложением каждого из них с первым, умноженным на - , - ,…, - . Таким образом, получаем [2]:

 

 (1.2.1)

 

В общем виде формулы для данного этапа выглядят следующим образом [2]:

 

 ,

 , (i,j=2…n)

На втором этапе проделаем то же самое, только первую строку в расчет не берем. Делим все элементы второй строки на , а затем исключаем переменную х2 из оставшихся строк путем опять же замены всех уравнений, начиная с третьего, уравнениями, полученными сложением каждого из них со вторым, умноженным на - , - ,…, - . Таким образом, получаем [2]:

 

 (1.2.2)

 

Формулы в общем виде[2]:

 

 , (i,j=3…n)

 

Этот процесс продолжается до тех пор, пока матрица не будет приведена к виду [2]:

 

 (1.2.3)

 

Коэффициенты данной системы получены по формулам [2]:

 , (i, j=k+1…n, k=1…n-1)

 

Все рассмотренные выше этапы называются прямым ходом метода Гаусса. Далее идет обратный ход: значения х вычисляются снизу вверх по формуле [2]:

 

, (k=n,n-1,…,1)

 

LU-разложение матриц

Данный метод напрямую связан с методом Гаусса. В предыдущем пункте решение линейной системы сводилось к тому, что матрицу (1.1.3) путем элементарных преобразований сводили к верхней треугольной матрице (1.2.3). Заметим, что, умножая исходную матрицу на матрицу (1.2.3), получится нижняя треугольная матрица с единицами на главной диагонали [5]. Учитывая эту взаимосвязь, можно подойти к решению линейной системы иначе, то есть, разложив исходную матрицу в произведение двух треугольных матриц А=LU [5, 7]:

 

 (1.3.1)

 

То есть систему Ax=b можно переписать в виде:

LUx=b (1.3.2)

 

Введем вектор вспомогательных переменных  и (1.3.2) перепишем в виде [2, 7]:

 

 (1.3.3)

 

Очевидно, чтобы найти х, нужно сначала найти у. Для этого запишем первое уравнение (1.2.3) в развернутом виде:

 

 (1.3.4)

 

Найти у можно сверху вниз по формуле [7]:

 

 при i=1,2,…,n. (1.3.5)

 

Аналогично для второго уравнения (1.3.3):

 

 (1.3.6)

Найти у можно снизу вверх по формуле [7]:

 

 при i=n,n-1,…,1 (1.3.7)

 

Метод прогонки решения систем с трехдиагональными матрицами коэффициентов

Данный метод удобно применять для так называемых ленточных трёхдиагональных матриц вида [10]:

 

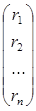* = (1.4.1)

 

Каждое уравнение такой системы связывает три «соседних» неизвестных [2, 10]:

 

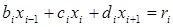, где i=1…n; b1=0; dn=0. (1.4.2)

 

Предположим, что существуют такие наборы чисел  и  (i=1…n), при которых [10]

 

 (1.4.3)

 

Уменьшим индекс на единицу, подставим полученное в (1.4.2) и выразим хi [2,10] :

 (1.4.4)

 

Сравнив (1.4.3) и (1.4.4), получаем, что [10]:

 

 (1.4.5)

 

при i=1…n - прямая прогонка,

при i=n…1 - обратная прогонка.

Эти коэффициенты называются прогоночными. Найдя их по формулам (1.4.5), можно найти хi из формулы (1.4.3).