Метод вращений решения линейных систем

Цель данного метода - привести систему (1.1.1) к треугольному виду (как в методе Гаусса).

Пусть 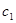 и 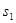 - некоторые отличные от нуля числа. Умножим первое уравнение системы (1.1.1) на 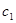, а второе - на  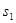и сложим строки, записав результат в первую строку. Затем умножим первую строку исходной системы на - 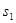, а вторую - на 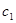, сложим их и результат запишем во вторую строку. Таким образом, наша система преобразуется к виду [8]:

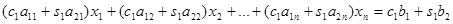 (1.5.1)

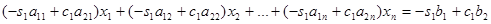
На введенные параметры накладываются 2 условия [8]:

условие обнуления (исключения х1 из второго уравнения)

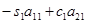=0 (1.5.2)

условие нормировки. За 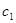 и 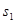 можно принять соответственно

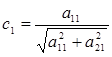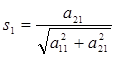,  (1.5.3)

Отсюда система (1.1.1) принимает вид [8]:

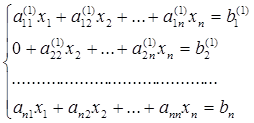 (1.5.4)

Где 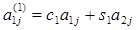 (j=1…n)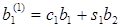  

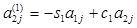 (j=2…n)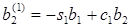

Далее первое уравнение системы (1.5.4) заменяется новым, полученным сложением результатов умножения первого и третьего уравнений на [8]:

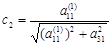 и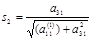  

А третье уравнение системы (1.5.4) заменим полученным сложением результатов умножения тех же уравнений, умноженных на - 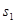и 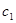. Таким образом, получаем систему [8]:

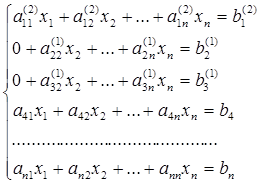 (1.5.5)

где 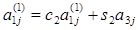 (j=1…n)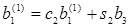

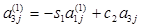 (j=2…n)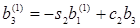

Проделав такие преобразования n-1 раз мы обнулим коэффициенты при х1 в первом столбце, кроме первой строчки. Затем проделаем аналогичные преобразования с остальными столбцами и в конечном итоге получим треугольную матрицу. После этого можно будет найти неизвестные. Это делается точно так же как в обратном методе Гаусса.

Глава 2. Метод квадратного корня для решения линейных систем

Краткая характеристика метода

Метод квадратного корня применяется в том случае, когда матрица А симметричная, то есть:

= aji (i, j = 1, 2, …, n).

Кроме того, матрица должна быть невырожденной, то есть её определитель не должен равняться нулю (det(A)¹0). Таким образом, система будет иметь единственное решение.

Метод квадратного корня дает большой выигрыш во времени по сравнению с другими методами (например, методом Гаусса), так как, во-первых, существенно уменьшает число умножений и делений (почти в два раза для больших n), во-вторых, позволяет накапливать сумму произведений без записи промежуточных результатов.

Всего метод квадратных корней требует [2,3] 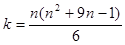 операций умножения и деления (примерно в два раза меньше, чем метод Гаусса), а также n операций извлечения корня.

Постановка задачи

К решению систем линейных уравнений сводятся многочисленные практические задачи. Запишем еще раз систему (1.1.1) n линейных алгебраических уравнений с n неизвестными [4]:

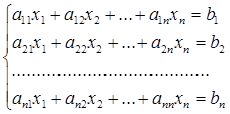
Совокупность коэффициентов (aij), неизвестных (хi) и свободных членов (bi) этой системы запишем в виде матриц (1.1.2) [4]:

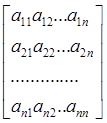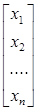= , X= , B=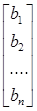

Используя понятие матрицы , систему уравнений (1.1.1) можно записать в матричном виде:

=b (2.2.1)

Таким образом, задача состоит в том, чтобы вычислить столбец неизвестных, используя метод квадратного корня.