Возмущение при наличии вырождения

В большинстве важных в приложениях задач приходится встречаться со случаем вырождения, когда в невозмущенной системе ( H ) собственному значению  E = E принадлежит не одно состояние j , а несколько j , j …, j …., j . Если теперь действует некоторое возмущение W, то без специального исследования нельзя сказать, какая из функций j будет являться нулевым приближением к собственным функциям оператора H = Y + W. В самом деле, вместо ряда функций j …, j …., j , принадлежащих собственному значению E , могут быть взяты функции j , j …, j …., j , получающиеся из первых линейным ортогональным преобразованием:

                                                                                         (68.1)

                                                                                       (68.2)
Функции j , будучи линейными комбинациями функций j , будут также решением уравнения Шредингера

                                                                                         (68.3)
принадлежащим собственному значению E , и при добавочном условии (68.2) будут ортогональными, если функции j ортогональны. Функции  j суть поэтому также возможные функции нулевого приближения, но неизвестно, какие коэффициенты a следует взять, чтобы получить правильное нулевое приближение.

Для решения этого вопроса обратимся к уравнению (66.9). Нам, однако, следует теперь его несколько модифицировать, уточнив обозначения. При наличии вырождения собственные функции оператора имеют по крайней мере два индекса (n, a). Поэтому в этом случае (66.4) следует написать подробнее, заменяя индекс n на два: n, a. Тогда мы получим

                                                                                         (68.4)
Соответственно этому уравнение (66.9) получится (заменяя n на n, a, m на m, b) в виде

                                                                                         (68.5)
где

                                                                                         (68.6)
есть матричный элемент энергии возмущения и получается из (66.7) увеличением числа квантовых чисел, нумерующих состояния. E есть энергия m-го квантового уровня для невозмущенной задачи. Эта энергия от квантового числа a не зависит (вырождение).

Допустим, что мы теперь желаем найти квантовый уровень возмущенной системы E , близкий к E , и соответствующие собственный функции j ( x). Ограничимся решением этой задачи в первом приближении для уровней и в нулевом приближении для функций.

В отсутствии вырождения мы полагали для функций нулевого приближения, что они просто совпадают с невозмущенными. Соответственно этому в нулевом приближении c = 1, а остальные равны 0. Этого нельзя сделать при наличии вырождения, ибо, отбрасывая в нулевом приближении возмущение W, мы получим из (68.5)

это дает c = 0 для E = E , но при это не одно c , а все принадлежащие собственному значению E , именно, c  для b = 1, 2, …, . Таким образом, в нулевом приближении не одна амплитуда, а целая группа отлична от нуля. Поэтому правильным нулевым приближением для функций k-го уровня будет

                                                                                    (68.7)
В этом приближении мы возьмем из уравнений (68.5) те, которые содержат не равные нулю c . Это будут уравнения

                                                                                         (68.8)
Поскольку мы ограничиваемся нулевым приближением к k-му уровню, мы можем опустить индекс k (держа его просто в уме), положив при этом

                                                                                         (68.9)

                                                                                         (68.9')
Тогда уравнения (68.8) запишутся в виде

                                                                                         (68.10)
У  E мы сохранили индекс k, чтобы подчеркнуть все же, что речь идет о группе из f состояния, принадлежащих уровню E .

Для того чтобы уравнения (68.10) имели отличные от нуля решения, необходимо, чтобы определитель системы (68.10) обращался в нуль, т.е.

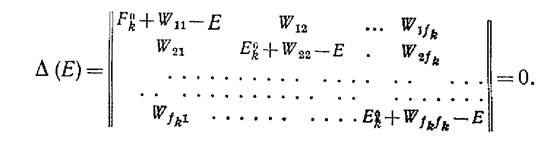
Это ¾ алгебраическое уравнение степени f для определения Е. Часто оно называется вековым[2] уравнением. Из него мы получим f корней:

                                                                                                (68.12)
Так как матричные элементы W предполагаются малыми, то эти корни будут близки между собой. Следовательно, мы получает важный результат: при наложении возмущения вырожденный уровень ( E ) распадается на ряд близких уровней (68.12). Вырождение снимается. Если некоторые из корней (68.12) равны, то вырождение снимается лишь частью.

Для каждого из корней E (68.12) мы получим свое решение для амплитуд c из уравнения (68.10). Чтобы отметить, что решение c , c , …, c . …, c  принадлежит уровню E , мы введем в c еще один индекс a так, что решение уравнений (68.10) для E запишется в виде

                                                                                                     (68.13)
Если бы мы еще удержали индекс k, то полная нумерация для  c была бы  c . Уравнение (68.13) есть приближенная (в нулевом приближении) волновая функция оператора Н в "Е ° "-представлении. В "х"-представлении решение (68.13) запишется в виде

                                                                                                     (68.13')
Таким образом, каждому уровню E = E   принадлежит теперь своя функция j  , которая и является функцией нулевого приближения для возмущенной системы (H).

Отличие функций (68.13') от функций (68.1) состоит в том, что в (68.1) коэффициенты a  произвольны (вплоть до условия ортогональности (68.2)), а коэффициенты c     в (68.13) определены. Следовательно, функции нулевого приближения j представляют собой частный случай функций невозмущенной задачи j . Заметим, что если вычислить следующие приближения, то нетрудно убедиться, что условием пригодности метода теории возмущения будет опять-таки (67.13), которое теперь для вырожденного случая будет иметь вид

                                                                                         (68.14)

В #41 было показано, что задача нахождения собственных значений и собственных функций любого оператора L, заданного в матричной форме, сводится к решению уравнение (41.4) и (41.5). Понимания в (41.4) под оператором L оператор полной энергии H, мы должны учитывать, что в случае вырождения вместо каждого из индексов n и m в этой формуле теперь фигурирует по два индекса n, a, и m, b соответственно. В результате из (41.4) получаем уравнения

                                                                                               (68.15)
которые совпадают с (68.5), так как

                                                                                                     (68.16)
Уравнение (41.5), соответствующее системе (41.4), в нашем случае запишется несколько сложнее (по форме), так как строки и столбцы матрица оператора Н нумеруются двумя квантовыми числами n и a. Именно, при каждом n имеется f разных значений a  (f -кратное вырождение). Число f   возрастает с увеличением n. Для первого уровня  f   = 1 термин "вырождение" не применяется.

Расположить элементы H  в матрицу не представляет труда. Так, можно нумеровать какой-нибудь столбец парой (1), а следующие столбцы номерами (n, 2), (n, 3), …, (n, f ) затем пойдет столбцы с номерами (n + 1, 1)(n + 1, 2), …, до (n + 1, f )и т.д. Подобным же образом нумеруем строки (m, 1), (m, 2),…, (m, f ) и т.д. При такой же нумерации элементов матрицы
H       уравнение для определения собственных значений E может быть написано в следующем виде (это и есть уравнение (41.5) для нашего случая):

Обведенные прямоугольниками матричные элементы относятся к одному и тому же квантовому уровню. Так, например, в первом прямоугольнике (один элемент) ¾ к уровню k = 1, во втором к уровню k = 2, в третьем ¾ к k-му уровню. Если мы пренебрежем матричными элементами, относящимися к различным уровням, т.е. элементами типа H    ( m = n ) (эти элементы, согласно (68.16), равны W   ), то уравнение (68.17) упростится и примет вид.

Такую матрицу называют ступенчатой. Ее определитель      (E) разбивается на произведение определителей меньшего ранга, именно [3],

Обозначая входящие сюда определители через    (E), получим

                                                                             (68.20)
Уравнение (68.20) будет удовлетворено, если (E) = 0, или     (E) = 0, или вообще  (E) = 0. Корни этих уравнений и дают в первом приближении энергии первого, второго и вообще k-го уровня. Уравнение

                                                                                         (68.12)
тождественно с уравнением (68.11), установленным другим путем.

В #41 мы объясняли, что задача нахождения собственных значений оператора может рассматриваться как задача о приведении к диагональному виду его матрицы. Из изложенного видно, что принимаемое в теории возмущения первое приближение заключается в том, что мы пренебрегаем матричными элементами, относящимися к разным уровням, и, таким образом, задачу о приведении к диагональному виду бесконечной матрицы сводим к приведению к диагональному виду конечных матриц (отдельных матриц в ступенчатой матрице (68.18)).