Корреляционно-регрессионный анализ. Уравнение парной регрессия: экономическая интерпретация и оценка значимости

Основная задача корреляционного анализа заключается в выявлении взаимосвязи между случайными переменными путем точечной и интервальной оценки парных (частных) коэффициентов корреляции, вычисления и проверки значимости множественных коэффициентов корреляции и детерминации. Кроме того, с помощью корреляционного анализа решаются следующие задачи: отбор факторов, оказывающих наиболее существенное влияние на результативный признак, на основании измерения степени связи между ними; обнаружение ранее неизвестных причинных связей. Корреляция непосредственно не выявляет причинных связей между параметрами, но устанавливает численное значение этих связей и достоверность суждений об их наличии.

Регрессионный анализ предназначен для исследования зависимости исследуемой переменной от различных факторов и отображения их взаимосвязи в форме регрессионной модели.

В регрессионных моделях зависимая (объясняемая) переменная Y может быть представлена в виде функции f (X₁, X₂, X₃, … Xm), где X₁, X₂, X₃, … Xm - независимые (объясняющие) переменные, или факторы. В качестве зависимой переменной может выступать практически любой показатель, характеризующий, например, деятельность предприятия или курс ценной бумаги. В зависимости от вида функции f (X₁, X₂, X₃, … Xm) модели делятся на линейные и нелинейные. В зависимости от количества включенных в модель факторов Х модели делятся на однофакторные (парная модель регрессии) и многофакторные (модель множественной регрессии).

Связь между переменной Y и m независимыми факторами можно охарактеризовать функцией регрессии Y= f (X₁, X₂, X₃, … Xm), которая показывает, каково будет в среднем значение переменной y_i, если переменные x_i примут конкретные значения.

Данное обстоятельство позволяет использовать модель регрессии не только для анализа, но и для прогнозирования экономических явлений.

Под линейностью здесь имеется в виду, что переменная y предположительно находиться под влиянием переменной x в следующей зависимости:

,

где 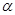 - постоянная величина (или свободный член уравнения), - коэффициент регрессии, определяющий наклон линии, вдоль которой рассеяны данные наблюдений. Это показатель, характеризующий изменение переменной , при изменении значения  на единицу. Если  - переменные и  положительно коррелированные, если < 0 – отрицательно коррелированны; - независимые одинаково распределенные случайные величины – остаток с нулевым математическим ожиданием ( ) и постоянной дисперсией ( ). Она отражает тот факт, что изменение  будет неточно описываться изменением Х – присутствуют другие факторы, неучтенные в данной модели.

Для оценки параметров регрессионного уравнениянаиболее часто используют метод наименьших квадратов (МНК), который минимизирует сумму квадратов отклонения наблюдаемых значений от модельных значений .

Согласно принципу метода наименьших квадратов, оценки  и  находятся путем минимизации суммы квадратов

по всем возможным значениям  и  при заданных (наблюдаемых) значениях . Задача сводится к известной математической задаче поиска точки минимума функции двух переменных. Точка минимума находится путем приравнивания нулю частных производныхфункции  по переменным  и . Это приводит к системе нормальных уравнений

решением которой и является пара , . Согласно правилам вычисления производных имеем

так что искомые значения ,  удовлетворяют соотношениям

Эту систему двух уравнений можно записать также в виде

Эта система является системой двух линейных уравнений с двумя неизвестнымии может быть легко решена, например, методом подстановки. В результате получаем

 (3.2)   

Такое решение может существовать только при выполнении условия

что равносильно отличию от нуля определителя системы нормальных уравнений. Действительно, этот определитель равен

Последнее условие называется условием идентифицируемостимодели наблюдений , и означает, что не все значения  совпадают между собой. При нарушении этого условия всеточки 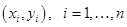, лежат на однойвертикальной прямой

Оценки  и  называют оценками наименьших квадратов. Обратим еще раз внимание на полученное выражение для . Нетрудно видеть, что в это выражение входят уже знакомые нам суммы квадратов, участвовавшие ранее в определении выборочной дисперсии

Для двух переменных теоретический коэффициент корреляции определяется следующим образом:

.

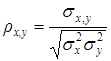где - дисперсии случайных переменных , а  их ковариация.

Парный коэффициент корреляции является показателем тесноты связи лишь в случае линейной зависимости между переменнымии обладает следующими основными свойствами:

Коэффициент корреляции принимает значение в интервале (-1,+1), или

| r _xy | < 1.

Коэффициент корреляции не зависит от выбора начала отсчета и единицы измерения, т.е.

r (α₁X+β; α₂Y+β)= r_xy,

где α_1, α₂, b - постоянные величины, причем α₁>0_, α₂>0.

Случайные величины Х, Y, можно уменьшать (увеличивать) в α раз, а также вычитать или прибавлять к значениям одно и тоже число β - это не приведет к изменению коэффициента корреляции r.

При r = ±1 случайные величины связаны линейной зависимостью, т.е.

.

При r = 0 линейная корреляционная связь отсутствует.

В практических расчетах коэффициент корреляции r генеральной совокупности обычно не известен. По результатам выборки может быть найдена его точечная оценка – выборочный коэффициент корреляции r, так как выборочная совокупность переменных случайна, то в отличие от параметра r , r – случайная величина. Оценкой коэффициента корреляции 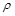 является выборочный парный коэффициент корреляции:

  = , (3.3)

Для оценки значимости коэффициента корреляции применяется t - критерий Стьюдента. При этом фактическое значение этого критерия определяется по формуле:

 (3.4)

Вычисленное по этой формуле значение t_набл сравнивается с критическим значением t-критерия, которое берется из таблицы значений t Стьюдента с учетом заданного уровня значимости и числа степеней свободы.

Если t_набл > t_кр, то полученное значение коэффициента корреляции признается значимым (то есть нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается). И таким образом делается вывод о том, что между исследуемыми переменными есть тесная статистическая взаимосвязь.

Если значение  близко к нулю, связь между переменными слабая. Если случайные величины связаны положительной корреляцией, это означает, что при возрастании одной случайной величины другая имеет тенденцию в среднем возрастать. Если случайные величины связаны отрицательной корреляцией, это означает, что при возрастании одной случайной величины, другая имеет тенденцию в среднем убывать.