Л.2. Вопрос №2. Метод вращающегося поля для трехфазного напряжения

Предлагаемый Способ определения частоты трехфазного напряжения поясняется с помощью прилагаемых чертежей (фиг.1-3), на которых сделаны следующие обозначения.

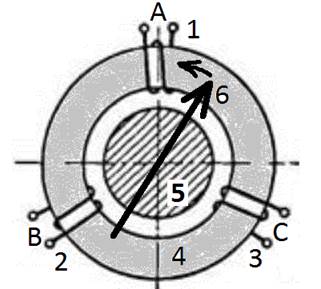
Фиг.1

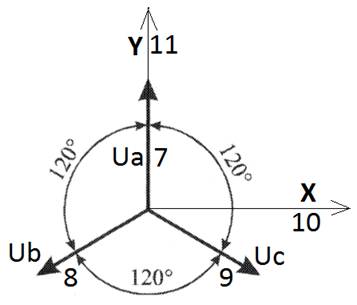
Фиг.2

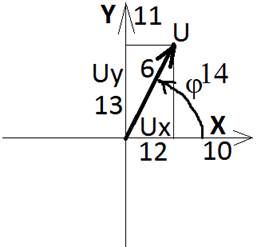
Фиг.3

· Катушки статора двигателя фазы A (1), В (2), С (3), к которым подключено трехфазное напряжение Ua, Ub, Uc.

· Катушки статора двигателя A (1), В (2), С (3) намотаны на магнитопровод статора 4.

· Токи, протекающие по катушкам 1, 2, 3 создают в роторе 5 вращающееся поле U (6).

· Три вектора напряжения Ua (7), Ub (8), Uc (9), между которыми имеется угол 120 градусов, создают проекции на прямоугольную систему координат, с осями Х (10), Y (11).

· Проекции векторов Ua (7), Ub (8), Uc (9) на оси Х (10), Y (11) создают координаты Ux (12), Uy (13) вращающегося вектора U (6), который имеет угол φ (14) относительно оси Х (10).

Сущность изобретения заключается в следующем. Принцип работы промышленных трехфазных сетей 50 герц связан с подачей на двигатель трехфазного напряжения Ua (7), Ub (8), Uc (9). Токи, протекающие по катушкам фаз A (1), В (2), С (3) статора 4 двигателя, к которым подключено трехфазное напряжение Ua (7), Ub (8), Uc (9), создают в роторе 5 двигателя вращающееся поле U (6), последнее и вращает ротор 5 двигателя.

Соответственно частотой F трехфазной сети является частота вращения поля U (6), угол φ (14) которого относительно оси Х (10) непрерывно увеличивается с вращением поля U (6). Увеличение угла φ (14) на угол 2π происходит за один оборот поля U (6), или за период Т частоты F=1/T. Подсчитав скорость изменения угла φ (14) найдем частоту F трехфазного напряжения Ua (7), Ub (8), Uc (9).

Координаты Ux (12), Uy (13) вращающегося вектора U (6) получаются из проекций векторов Ua (7), Ub (8), Uc (9) на оси Х (10), Y (11):

Ux = (Uc – Ub)·√3/2,

Uy = Ua – (Ub+ Uc)/2

Модуль (длина) вектора U (6) определяется из координат Ux (12), Uy (13):

U = √( U²x + U²y)

    Для определения частоты F трехфазного напряжение Ua (7), Ub (8), Uc (9) в микропроцессорных терминалах используются цифровые сигналы всех трех фаз Ua(t_i), Ub(t_i), Uc(t_i) промышленного трехфазного напряжения, измеренные в моменты времени t_i, где i - целое значение, оцифрованные с периодом дискретизации dt=(t_i - t_i-1 ). Причем величина dt значительно меньше периода T наибольшей частоты Fв=1/T диапазона измерения частоты F, dt<<T.

В каждый момент времени t_i определяется проекция Ux(t_i) на ось абсцисс Х вращающегося поля U(t_i), создаваемого тремя фазами Ua(t_i), Ub(t_i), Uc(t_i) промышленного трехфазного напряжения, по формуле:

Ux(t_i)= ,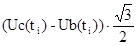

определяется проекция Uy(t_i) на ось абсцисс Y вращающегося поля U(t_i):

Uy(t_i)= ,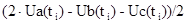

определяется модуль вращающегося поля U(t_i):

U(t_i)= ,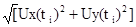

определяется зависимость от времени t_i приращение фазы dφ_i вращающегося поля U(t_i) за интервал dt=(t_i - t_i-1 ), по формуле:

|dφ_i |= |φ(t_i) - φ(t_i-1)|=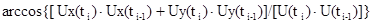

Приращение dφ_i , вычисляемое с использованием тригонометрической функции arcos(), будет всегда положительным. Поэтому для определения знака dφ_i проведем дополнительные вычисления.

· Если | Ux(t_i)| ≤ | Uy(t_i)|, то знак dφ_i равен знаку величины

Uy(t_i) · [Ux(t_i-1)-Ux(t_i)],

· Если | Ux(t_i)| > | Uy(t_i)|, то знак dφ_i равен знаку величины

Ux(t_i) · [Uy(t_i)-Uy(t_i-1)].

Для повышения точности измерения частоты F(t_i) определяется среднее за интервал времени n·dt значение частоты F(t_i) в момент времени t_i, по формуле:

F(t_i) = ( 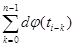)/(2π·n·dt), где n – целое значение.

Л.3. Вопрос №1-2. Метод вращающегося поля для однофазного напряжения

Методом синхронного детектирования (квадратурный детектор, или определение первой гармоники методом Фурье преобразования) из однофазного напряжения получаем его представление в виде идеальной синусоиды.

Сигнал S(t) называется периодическим, если все его значения повторяются через промежуток времени k*T, где T – наименьший период повторения сигнала, k – целое значение. Такой сигнал можно разложить в гармонический ряд Фурье:

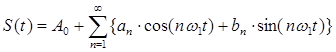
где: 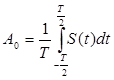 (1) – постоянная составляющая сигнала,  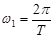(2) – циклическая частота первой гармоники, обратно пропорциональна периоду сигнала,

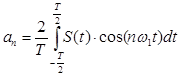 (3)

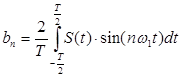 (4)

U=Uo*sin(ɷ*t+φ),

где Uo – амплитуда вращающегося с частотой ɷ вектора, со сдвигом фазы φ.

или в комплексном виде:

U= Re(X)+j*Im(X),

где Re(X) и Im(X) проекции вращающегося вектора на реальную и мнимую оси.

U²o= Re²(X) + Im²(X)

Re(X) = Uo*cos(φ)

Im(X) = Uo*sin(φ)

Тогда можем найти частоту:

φ = arctg(Im(X)/ Re(X))

Производная от арктангенса arctg(x) это 1/(1+x^2).

Производная от сложной функции g(f(t)) это g’(f) * f’(t).

Ну и производная от частного u(t)/v(t) это (u’*v - v’*u)/v^2

Если все это учесть, получаем следующее:

φ’ = 1/(1+Im(X)^2/Re(X)^2) * (Im’(X)*Re(X) – Re’(X)*Im(X)) / Re(X)^2
φ’ = Re(X)^2 / (Re(X)^2 + Im(X)^2) * (Im’(X)*Re(X) – Re’(X)*Im(X)) / Re(X)^2
φ’ = (Im’(X)*Re(X) – Re’(X)*Im(X)) / |X|^2

Из производной угла найдем частоту:

ɷ= φ’/2π либо ɷ= ɷo + φ’/2π (если при подсчете Фурье преобразования время будет непрерывно возрастать)

где ɷ_o – опорная частота, при которой подсчитывается Re(X) и Im(X).