 |
Главная |
Простейшим способом задания конечного множества М из
|
из
5.00
|
𝑛 элементов является прямое перечисление его элементов в фигурных скобках с их нумерацией
М= 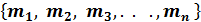 . .
|
Пример: М={2, 0, -3}={0, -3, 2}. Перестановкой элементов множества подчеркивается произвольность порядка их перечисления.
Если множество М бесконечно, но, тем не менее, все его элементы можно перенумеровать, то такое множество называется счетным и оно может быть представлено в аналогичном виде
М=  . .
|
Помимо перечисления элементов множества можно описывать с помощью, так называемого характеристического свойства (признака), которое означает справедливость (истинность) некоторого утверждения только для элементов данного множества.Обозначим характеристическое свойство символом XS. Тогда множество М описывается как совокупность неких объектов, обладающих свойством XS:
М= 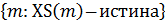 . .
|
Возможна также запись
М= 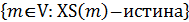 , ,
|
которая означает, что множество М состоит из тех элементов множества V, для которых утверждение 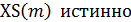 .
.
Например, V= 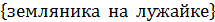 ,а ХS - “спелость”. Тогда
,а ХS - “спелость”. Тогда
М - все спелые ягоды земляники на этой лужайке.
Математика имеет дело с множествами различной природы и, конечно же, с числовыми множествами, для которых приняты стандартные обозначения:
N - множество натуральных чисел (целых больших нуля);
Z - множество всех целых чисел (положительных и отрицательных);
Q - множество рациональных чисел (получаемых в результате
деления двух целых чисел);
R - множество вещественных или действительных чисел
(рациональных чисел в совокупности с иррациональными -
корнями из рациональных чисел).
Теперь, используя рассмотренные выше способы, нетрудно дать формализованное описание этих множеств:
N=  ;
;
Z= 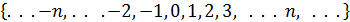 ;
;
Q= 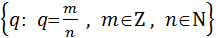 =
=  ;
;
R= 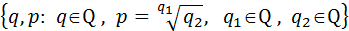 .
.
Множество вещественных положительных чисел как подмножество всех вещественных чисел может быть описано следующей фразой
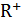 =
= 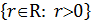 ÌR,
ÌR,
где ” 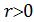 ” - характеристический признак.
” - характеристический признак.
Для двух множеств X и Y совокупность упорядоченных пар (𝑥, 𝑦), первый элемент которой принадлежит первому множеству, а второй - второму называется декартовым или прямым произведением указанных множеств и обозначается
X×Y= 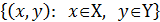 . .
|
В частности, декартово произведение самого на себя множества вещественных чисел как точек числовой оси дает геометрическую плоскость в виде множества точек в координатном представлении
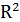 =R×R=
=R×R= 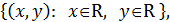
где линия 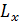 =
= 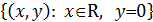 является осью абсцисс, а
является осью абсцисс, а
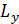 =
= 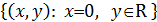 - осью ординат.
- осью ординат.
Примеры.
1. Пустое множество
V= 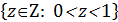 =Æили U=
=Æили U= 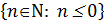 =Æ.
=Æ.
2. Множество целых чисел на интервале [0, 3)
C=  =
= 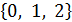 .
.
3. Интервал [-5, 3)={  : -5£ 𝑥<3}.
: -5£ 𝑥<3}.
|
| -1 |
| S |
S={ 
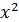 +
+ 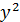 ≤1,
≤1, 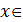 [-1, 0],
[-1, 0],  }.
}.
| (-2, 1) |
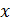 Î[-2, 0], Î[-2, 0],
|
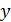
|
| - 2 |
декартово произведение двух отрезков
Р={( 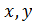 ):
): 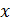 Î[-2,0],
Î[-2,0], 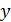 Î[0,1] }=[-2,0]´[0,1].
Î[0,1] }=[-2,0]´[0,1].
6. Прямое произведение двух конечных числовых множеств
А={1, 0, -3} и В={2, -3} дает 6 числовых пар
А´В={(1,2), (1,-3), (0,2), (0,-3), (-3,2), (-3,-3)}.
| В´А≠ А´В. |
{(2,1), (2,0), (2,-3), (-3,1), (-3,0), (-3,-3)} =
Неравенство в рамке означает, что декартово произведение не обладает свойством перестановочности множеств (коммутативность).
|
из
5.00
|
Обсуждение в статье: Простейшим способом задания конечного множества М из |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

