Операции над матрицами. Матрицы одинакового размера можно складывать и умножать на числа

Матрицы одинакового размера можно складывать и умножать на числа. Множество всех матриц размера относительно этих операций образует линейное пространство размерности , причем каноническими координатами являются матричные элементы.

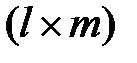Если размеры матриц и и соответственно, то есть число столбцов матрицы совпадает с числом строк матрицы , то можно определить произведение матриц и . Матричный элемент матрицы вычисляется по формуле:

,

то есть равен произведению строки матрицы с номером на столбец матрицы с номером .

У матрицы число строк такое же, как у матрицы 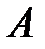, а число столбцов такое же, как у матрицы , то есть матрица имеет размер .

Умножение матриц не коммутативно, то есть, как правило, 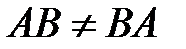, поэтому говорят об умножении матрицы слева или справа на матрицу .

При умножении матриц роль единицы играют квадратные матрицы, у которых на главной диагонали стоят 1, а на остальных местах 0. Такие матрицы называются единичными и обозначаются символом .

Операция умножения на матрицу обладает свойствами линейности и ассоциативности, то есть:

;

.

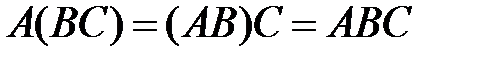Отметим, что для квадратных матриц выполняется теорема об умножении определителей .

Матрица называется транспонированной к матрице , если ее строки являются столбцами матрицы 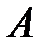с теми же номерами, а столбцы – строками. Матричный элемент 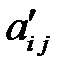матрицы равен .

Операция транспонирования обладает следующими свойствами:

1) , 2) , 3) .

Квадратная матрица называется симметричной, если и кососимметричной, если .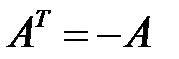

Обратная матрица

Матрица называется левой обратной к , если . Аналогично, называется правой обратной к , если . Если существуют левая и правая обратные к 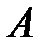матрицы, то они совпадают, то есть 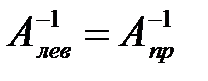. Эта матрица называется обратной к и обозначается . Для того, чтобы матрица имела обратную матрицу, необходимо и достаточно, чтобы она была невырожденной, то есть .

Если , то для вычисления можно использовать следующий алгоритм:

1. Строим матрицу , присоединенную к ( - алгебраические дополнения к в ).

2. Транспонируем полученную матрицу. Получаем матрицу .

3. Обратная матрица вычисляется по формуле .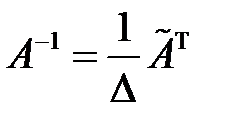

Матричные уравнения

1. Уравнения вида и . Если невырожденная матрица ( ), то решение первого уравнения дается формулой , а второго формулой .

2. Уравнения вида решаются аналогично, при условии, что и невырожденные матрицы. Решение дается формулой .

3. Уравнения п.п. 1 и 2 в случае вырожденности соответствующих матриц, а также уравнения вида сводятся к решению систем линейных уравнений относительно элементов матрицы .

Примеры решения типовых задач