 |
Главная |
Линейная зависимость и независимость векторов
|
из
5.00
|
Задача 1.Выяснить, является ли система векторов  линейно независимой. Систему векторов будем задавать матрицей системы, столбцы которой состоят из координат векторов.
линейно независимой. Систему векторов будем задавать матрицей системы, столбцы которой состоят из координат векторов.
 .
.
Решение.Пусть линейная комбинация  равна нулю. Записав это равенство в координатах, получим следующую систему уравнений:
равна нулю. Записав это равенство в координатах, получим следующую систему уравнений:
 .
.
Такая система уравнений называется треугольной. Она имеет единственное решение  . Следовательно, векторы
. Следовательно, векторы  линейно независимы.
линейно независимы.
Задача 2.Выяснить, является ли линейно независимой система векторов.
 .
.
Решение.Векторы  линейно независимы (см. задачу 1). Докажем, что вектор
линейно независимы (см. задачу 1). Докажем, что вектор  является линейной комбинацией векторов
является линейной комбинацией векторов  . Коэффициенты разложения
. Коэффициенты разложения  по векторам
по векторам  определяются из системы уравнений
определяются из системы уравнений
 .
.
Эта система, как треугольная, имеет единственное решение.
Следовательно, система векторов  линейно зависима.
линейно зависима.
Замечание. Матрицы, такого вида, как в задаче 1, называются треугольными, а в задаче 2 – ступенчато-треугольными. Вопрос о линейной зависимости системы векторов легко решается, если матрица, составленная из координат этих векторов, является ступенчато треугольной. Если матрица не имеет специального вида, то с помощью элементарных преобразований строк, сохраняющих линейные соотношения между столбцами, её можно привести к ступенчато-треугольному виду.
Элементарными преобразованиями строк матрицы(ЭПС) называются следующие операции над матрицей:
1) перестановка строк;
2) умножение строки на отличное от нуля число;
3) прибавление к строке другой строки, умноженной на произвольное число.
Задача 3. Найти максимальную линейно независимую подсистему и вычислить ранг системы векторов
 .
.
Решение.Приведем матрицу системы с помощью ЭПС к ступенчато-треугольному виду. Чтобы объяснить порядок действий, строчку с номером  преобразуемой матрицы обозначим символом
преобразуемой матрицы обозначим символом  . В столбце после стрелки указаны действия над строками преобразуемой матрицы, которые надо выполнить для получения строк новой матрицы.
. В столбце после стрелки указаны действия над строками преобразуемой матрицы, которые надо выполнить для получения строк новой матрицы.

 .
.
Очевидно, что первые два столбца полученной матрицы линейно независимы, третий столбец является их линейной комбинацией, а четвертый не зависит от двух первых. Векторы  называются базисными. Они образуют максимальную линейно независимую подсистему системы
называются базисными. Они образуют максимальную линейно независимую подсистему системы  , а ранг системы равен трем.
, а ранг системы равен трем.
Базис, координаты
Задача 4. Найти базис и координаты векторов в этом базисе на множестве  геометрических векторов, координаты которых удовлетворяют условию
геометрических векторов, координаты которых удовлетворяют условию  .
.
Решение. Множество  является плоскостью, проходящей через начало координат. Произвольный базис на плоскости состоит из двух неколлинеарных векторов. Координаты векторов в выбранном базисе определяются решением соответствующей системы линейных уравнений.
является плоскостью, проходящей через начало координат. Произвольный базис на плоскости состоит из двух неколлинеарных векторов. Координаты векторов в выбранном базисе определяются решением соответствующей системы линейных уравнений.
Существует и другой способ решения этой задачи, когда найти базис можно по координатам.
Координаты  пространства
пространства  не являются координатами на плоскости
не являются координатами на плоскости  , так как они связаны соотношением
, так как они связаны соотношением  , то есть не являются независимыми. Независимые переменные
, то есть не являются независимыми. Независимые переменные  и
и 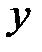 (они называются свободными) однозначно определяют вектор на плоскости и, следовательно, они могут быть выбраны координатами в
(они называются свободными) однозначно определяют вектор на плоскости и, следовательно, они могут быть выбраны координатами в  . Тогда базис
. Тогда базис  состоит из векторов, лежащих в
состоит из векторов, лежащих в  и соответствующих наборам свободных переменных
и соответствующих наборам свободных переменных  и
и  , то есть
, то есть  .
.
Задача 5. Найти базис и координаты векторов в этом базисе на множестве  всех векторов пространства
всех векторов пространства  , у которых нечетные координаты равны между собой.
, у которых нечетные координаты равны между собой.
Решение. Выберем, как и в предыдущей задаче, координаты в пространстве  .
.
Так как  , то свободные переменные
, то свободные переменные  однозначно определяют вектор из
однозначно определяют вектор из  и, следовательно, являются координатами. Соответствующий базис состоит из векторов
и, следовательно, являются координатами. Соответствующий базис состоит из векторов  .
.
Задача 6. Найти базис и координаты векторов в этом базисе на множестве  всех матриц вида
всех матриц вида  , где
, где  – произвольные числа.
– произвольные числа.
Решение. Каждая матрица из  однозначно представима в виде:
однозначно представима в виде:
 .
.
Это соотношение является разложением вектора из  по базису
по базису  с координатами
с координатами 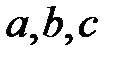 .
.
Задача 7.Найти размерность и базис линейной оболочки системы векторов
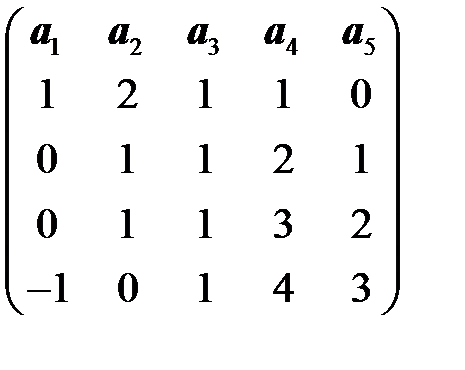 .
.
Решение.Преобразуем с помощью ЭПС матрицу из координат векторов системы к ступенчато-треугольному виду.
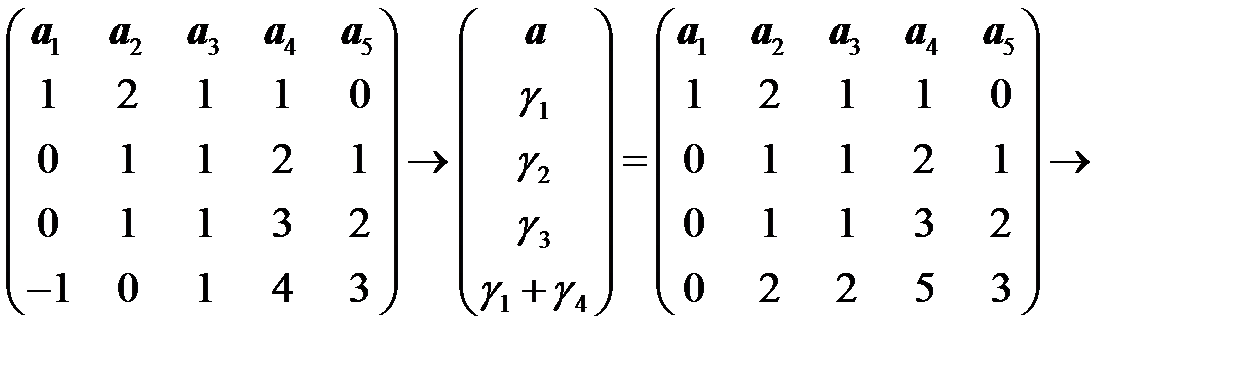
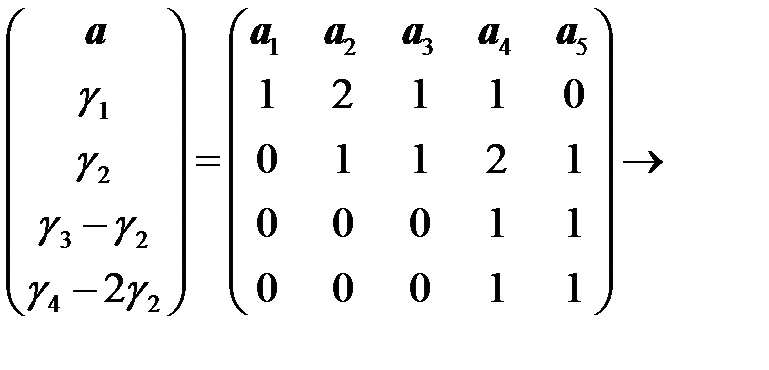
 .
.
Столбцы  последней матрицы линейно независимы, а столбцы
последней матрицы линейно независимы, а столбцы  линейно выражаются через них. Следовательно, векторы
линейно выражаются через них. Следовательно, векторы  образуют базис
образуют базис 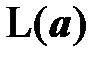 , и
, и  .
.
Замечание. Базис в 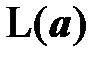 выбирается неоднозначно. Например, векторы
выбирается неоднозначно. Например, векторы  также образуют базис
также образуют базис  .
.
|
из
5.00
|
Обсуждение в статье: Линейная зависимость и независимость векторов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

