 |
Главная |
Определение скорости любой точки фигуры при плоском движении
|
из
5.00
|
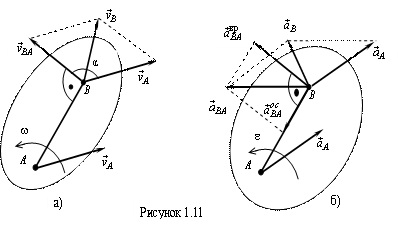
Скорость любой точки тела равна геометрической (векторной) сумме скорости полюса и скорости точки, приобретаемой ею при вращении тела вокруг полюса (рис. 1.11,а)
 (1.28)
(1.28)
Где  – вектор угловой скорости, введенный также, как и при рассмотрении вращения тела вокруг неподвижной оси (здесь этот вектор располагается на оси, проведенной через полюс перпендикулярно плоскости движения);
– вектор угловой скорости, введенный также, как и при рассмотрении вращения тела вокруг неподвижной оси (здесь этот вектор располагается на оси, проведенной через полюс перпендикулярно плоскости движения); 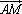 – радиус-вектор точки М, проведенный из точки А. Модуль вектора
– радиус-вектор точки М, проведенный из точки А. Модуль вектора
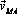 :
: 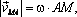 он направлен перпендикулярно отрезку AM в сторону вращения тела.
он направлен перпендикулярно отрезку AM в сторону вращения тела.
Численное значение скорости точки можно найти с помощью теоремы косинусов  или разложения на оси произвольно выбранной системы координат. Для определения скоростей точек тела при плоскопараллельном движении важную роль играет следующая теорема: «Проекции скоростей двух точек тела на прямую, соединяющую эти точки, равны». Заметим, что эта теорема справедлива для любого вида движения абсолютно твердого тела.
или разложения на оси произвольно выбранной системы координат. Для определения скоростей точек тела при плоскопараллельном движении важную роль играет следующая теорема: «Проекции скоростей двух точек тела на прямую, соединяющую эти точки, равны». Заметим, что эта теорема справедлива для любого вида движения абсолютно твердого тела.
24. Теорема о проекциях скоростей двух точек тела
Определение скоростей точек плоской фигуры (или тела, движущегося плоскопараллельно) связано обычно с довольно сложными расчетами. Однако можно получить ряд других, практически более удобных и простых методов определения скоростей точек фигуры (или тела).
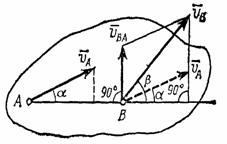 Рис.32
Рис.32
Один из таких методов дает теорема: проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу. Рассмотрим какие-нибудь две точки А и В плоской фигуры (или тела). Принимая точку А за полюс (рис.32), получаем 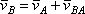 . Отсюда, проектируя обе части равенства на ось, направленную по АВ, и учитывая, что вектор
. Отсюда, проектируя обе части равенства на ось, направленную по АВ, и учитывая, что вектор  перпендикулярен АВ, находим
перпендикулярен АВ, находим
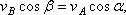
и теорема доказана.
25. Мгновенным центром скоростей (МЦС) называют точку подвижной плоскости, в которой расположено рассматриваемое сечение и скорость которой в данный момент времени равна нулю. Доказана теорема о том, что если тело движется не поступательно, то МЦС существует, и притом единственный. Из определения следует, что в общем случае в каждый момент времени МЦС находится в различных точках. Частным случаем является вращение тела вокруг неподвижной оси. Здесь МЦС расположен в любой момент времени на оси вращения. Если тело движется поступательно или мгновенно поступательно (скорости всех точек тела в данный момент времени равны по величине и направлению), то МЦС находится на бесконечно большом расстоянии от любой точки тела. Из векторной формулы (1.28) при определении скоростей любой точки плоской фигуры следует, что если в качестве полюса принять МЦС, т.е. 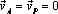 , то
, то 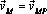 и скорость любой точки тела находится так, как если бы тело в данный момент времени вращалось вокруг неподвижной оси, проходящей через МЦС. Отсюда видно, что скорости точек тела пропорциональны их расстояниям до МЦС и перпендикулярны отрезкам, соединяющим эти точки с МЦС.
и скорость любой точки тела находится так, как если бы тело в данный момент времени вращалось вокруг неподвижной оси, проходящей через МЦС. Отсюда видно, что скорости точек тела пропорциональны их расстояниям до МЦС и перпендикулярны отрезкам, соединяющим эти точки с МЦС.
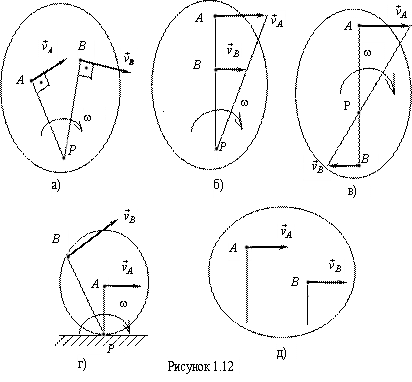
26. Способы определения положения мгновенного центра скоростей:
1) Если известны направления скоростей 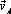 и
и 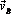 двух точек А и В плоской фигуры, то МЦС ее Р определяется как точка пересечения перпендикуляров к скоростям
двух точек А и В плоской фигуры, то МЦС ее Р определяется как точка пересечения перпендикуляров к скоростям 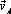 и
и 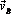 , проведенных из этих точек (рис. 1.12,а).
, проведенных из этих точек (рис. 1.12,а).
2) Если 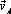 ||
|| 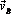 и точки A и B лежат на общем перпендикуляре к скоростям этих точек, то МЦС Р находится в точке пересечения прямой АВ с линией, соединяющей концы векторов скоростей
и точки A и B лежат на общем перпендикуляре к скоростям этих точек, то МЦС Р находится в точке пересечения прямой АВ с линией, соединяющей концы векторов скоростей 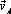 и
и 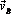 (см. рис. 1.12,б,в).
(см. рис. 1.12,б,в).
3) При качении без скольжения плоской фигуры по неподвижному контуру МЦС находится в точке соприкосновения контуров (см. рис. 1.12,г).
4) Если скорости двух точек A и B тела 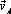 и
и 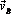 параллельны, а перпендикуляры к их скоростям не совпадают, то скорости всех точек тела равны, а МЦС Р находится в бесконечном удалении от этих точек и движение тела является мгновенно поступательным. Угловая скорость тела в данный момент времени равна нулю.
параллельны, а перпендикуляры к их скоростям не совпадают, то скорости всех точек тела равны, а МЦС Р находится в бесконечном удалении от этих точек и движение тела является мгновенно поступательным. Угловая скорость тела в данный момент времени равна нулю.
27. Ускорение любой точки тела равно геометрической сумме ускорения полюса и ускорения точки, приобретаемого ею при вращении тела вокруг полюса (см. рис. 1.11,б): 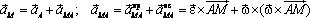 (1.29)
(1.29)
где 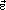 – вектор углового ускорения, введенный так же, как и при рассмотрении вращения тела вокруг неподвижной оси. Модули векторов
– вектор углового ускорения, введенный так же, как и при рассмотрении вращения тела вокруг неподвижной оси. Модули векторов 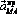 и
и 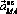 :
:
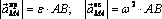
причем 1-й из них направлен перпендикулярно отрезку AB в сторону углового ускорения, а 2-й – к полюсу A. Определять модуль вектора ускорения точки B целесообразно аналитически с помощью разложения слагаемых векторов на оси выбранной системы координат.

28. Мгнове́нный центр ускоре́ний — при непоступательном движении точка, находящаяся в плоскости движения тела, ускорение которой в данный момент времени равно нулю.
Положение мгновенного центра ускорений в общем случае не совпадает с положением мгновенного центра скоростей. Однако в некоторых случаях, например, при чисто вращательном движении, положение этих двух точек может совпадать.
Для того, чтобы определить положение мгновенного центра ускорений, необходимо к векторам ускорений двух различных точек тела провести прямые под равными углами μ. В точке пересечения проведённых прямых и будет находиться мгновенный центр ускорений. Угол μ должен удовлетворять равенству:
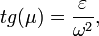
где
ε — угловое ускорение тела;
ω — угловая скорость тела.
|
из
5.00
|
Обсуждение в статье: Определение скорости любой точки фигуры при плоском движении |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

