 |
Главная |
Функциональные преобразователи
|
из
5.00
|
Функциональным преобразователем называется устройство, которое реализует правило, по которому заданному входному сигналу UВХ (t) ставится в соответствие заданный выходной сигнал UВЫХ (t). Правило преобразования (функция преобразования) может быть задано аналитически, графически или таблично.
6.3.1. Логарифмический преобразователь
Функция преобразования задаётся аналитически следующим соотношением: UВЫХ = aּlnUВХ + b.
Схема логарифмического преобразователя изображена на рис. 6.13.
В устройстве с глубокой отрицательной ОС разность потенциалов между двумя входами ОУ близка к нулю. Следовательно, анод диода имеет нулевой потенциал и справедливо выражение:
UД = – UВЫХ ,
где UД – напряжение на диоде, направленное от анода к катоду.

|
| Рис. 6.13. Логарифмический преобразователь |
Ток, протекающий через диод, находящийся в открытом состоянии, и напряжение на нём связаны соотношениями:
IД = I0ּexp(UД / φt),
где I0 – обратный ток диода.
Ln(IД / I0) = UД /φt ;
IД = UВХ / R1.
Используя полученные соотношения и проделав преобразования, получим следующую формулу:
UВЫХ = - φt ּLn UВХ + φt ּLn (I0ּR1). (6.13)
Таким образом, схема с ОУ, изображённая на рис. 6.13, осуществляет логарифмирование входного сигнала.
6.3.2. Экспоненциальный преобразователь
Функция преобразования задаётся аналитически следующим соотношением: UВЫХ = aּexp(bּUВХ).
Схема экспоненциального преобразователя изображена на рис. 6.14.

|
| Рис. 6.14. Экспоненциальный преобразователь |

 (6.14)
(6.14)
6.3.3. Линейно-ломаная функция
Линейно-ломаная функция (рис. 6.15), используемая, например, для детектирования АМ-сигналов, описывается выражением
 (6.15)
(6.15)

Обычно для реализации выражения (6.13) используют диодный однополупериодный детектор (рис. 6.16,а).
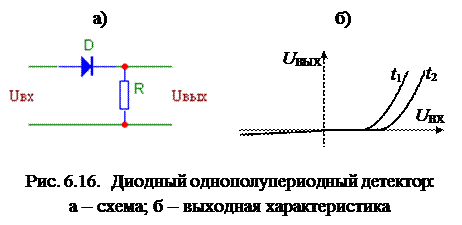 |
Однако его характеристика UВЫХ(UВХ) (рис. 6.16,б) существенно отличается от идеальной линейно-ломаной функции (рис. 6.15):
· характеристика имеет излом при UВХ = (0,6…0,7) В, а не при UВХ = 0, что не позволяет детектировать сигналы с малой амплитудой;
· точка излома существенно зависит от температуры;
· характеристика диода – экспоненциальная, а не линейная;
· UВЫХ ≠ 0 при UВХ < 0.
Идеальную линейно-ломаную характеристику даёт схема детектирования малых сигналов (рис. 6.17,а). Выходная характеристика имеет излом точно при UВХ = 0, сама характеристика строго линейна и не зависит от температуры (рис. 6.17,б).
| а) | б) |

|

|
| Рис. 6.17. Детектор малых сигналов: а – схема; б – выходная характеристика |
6.3.4. Функция произвольного вида
Любая нелинейная зависимость может быть аппроксимирована последовательностью прямых линейных отрезков, имеющих различные наклоны. Для примера попробуем аппроксимировать характеристику UВЫХ (UВХ) компрессора сигналов (рис. 6.18).
Структурная схема, реализующая такую функцию на ОУ, приведена на рис. 6.19.
При малой амплитуде UВХ ключи Кл-2 ÷Кл-n на рис. 6.17 разомкнуты, тангенс угла наклона первого участка характеристики на рис. 6.16, то есть модуль коэффициента передачи К1 , равен
 при
при 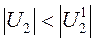 .
.

 |
При увеличении амплитуды UВХ замыкается ключ Кл-2 , параллельно резистору R2-1 подключается резистор R2-2, модуль коэффициента передачи К2 становится равен
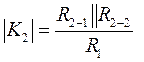 при
при  .
.
При дальнейшем увеличении амплитуды UВХ замыкается дополнительно ключ Кл-3 , параллельно резистору R2-1 подключается резисторы R2-2 и R2-3 , модуль коэффициента передачи К3 становится равен
 при
при  и так далее.
и так далее.
В реальной схеме, аппроксимирующей характеристику компрессора (рис. 6.20), роль ключей выполняют диодно-резистивные цепи. При UВХ < U11 диод D1 через резистор R3-2-1 заперт положительным напряжением Е1 (аналог разомкнутого ключа Кл-2). При UВХ > U11 диод D1 открывается (аналог замкнутого ключа Кл-2). По такому же принципу работают остальные диодно-резистивные ключи на рис. 6.20.
 |
Характеристика UВЫХ (UВХ) схемы компрессора приведена на рис. 6.21.
Для этой схемы 

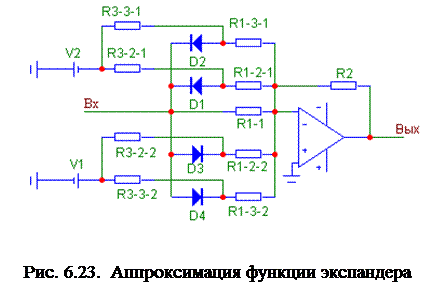
Зеркальная ей характеристика экспандера приведена на рис. 6.22, 6.23.
Для этой схемы  .
.

|
из
5.00
|
Обсуждение в статье: Функциональные преобразователи |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

