 |
Главная |
Активные RC-фильтры на основе ОУ
|
из
5.00
|
6.4.1. Общие положения
Электрическими фильтрами являются частотно-избирательные цепи, спроектированные для «пропускания» или передачи сигналов в одной или более непрерывных частотных полосах и заграждения сигналов в дополняющих полосах.
В зависимости от полосы частот пропускания фильтры классифицируются на:
· фильтры нижних частот (ФНЧ);
· фильтры верхних частот (ФВЧ);
· полосовые или полосно-пропускающие фильтры (ПФ) (рис. 6.24);
· частотно-выделяющие (или узкополосные) фильтры;
· частотно-подавляющие (или заграждающие) фильтры (ЗФ).
 |
Фильтры являются линейными устройствами, поскольку на их выходе не появляются новые спектральные составляющие. Традиционно описание фильтров производится в частотной области.
Рассмотримфильтр НЧ.
 |
АЧХ ФНЧ приведена на рис. 6.25, где:
К (f) = 1 в полосе пропускания ЕП, 0 < ЕП < f П ,
К (f) = 1 в полосе задерживания ЕЗ, f З < ЕЗ < ∞,
f П - верхняя граничная частота полосы пропускания ЕП,
f З - нижняя граничная частота полосы задерживания ЕЗ .
В интервале [f П , f З ] характер функции К (f) может быть различным.
АЧХ фильтра (рис. 6.25) мало информативна для расчёта и детального анализа фильтра. Обычно используют график ЧХ затухания (рис. 6.26).
 |
На рис. 6.26  (6.16)
(6.16)
amin – минимально - допустимое затухание полосе задерживания ЕЗ ;
δ – неравномерность затухания в полосе пропускания ЕП .
На рис.27 даны примеры простейших схем ФНЧ.
| а) | б) |

|

|
| Рис. 6.27. Примеры фильтров НЧ 1-го порядка: а – RC-фильтр; б - LR-фильтр |
У обеих схем крутизна спада АЧХ обратно пропорциональна частоте (p = jω), в логарифмическом масштабе спад АЧХ составляет 6 дБ на октаву (6 дБ/окт) или 20 дБ на декаду (20 дБ/дек); такие фильтры называют фильтрами первого порядка.
Для схемы рис. 27,а  .
.
Для схемы рис. 27,б 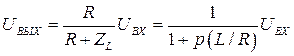 .
.
При двух реактивных элементах можно получить звено фильтра второго порядка со спадом АЧХ (или ростом затухания) 12 дБ/окт или 40 дБ/дек.
Другие типы фильтров. Ниже приведены АЧХ других типов фильтров: фильтра верхних частот ФВЧ (рис. 6.28,а), полосового фильтра ПФ (рис. 6.28,б), заграждающего фильтра ЗФ (рис. 6.28,в).
| а) | б) |

| 
|
 в) в)
| |
| Рис. 6.28. АЧХ других типов фильтров: а – ФВЧ; б – ПФ; в - ЗФ |
6.4.2. Аппроксимация активных RC фильтров
Поведение фильтра в частотной области описывается передаточной функцией Т(p), модуль которой  при p = jω, рассчитанный в заданной полосе частот, называется АЧХ. Так как значение АЧХ в полосе пропускания близко к единице, а в полосе задерживания много меньше 1, при расчёте используется характеристика затухания
при p = jω, рассчитанный в заданной полосе частот, называется АЧХ. Так как значение АЧХ в полосе пропускания близко к единице, а в полосе задерживания много меньше 1, при расчёте используется характеристика затухания
 (6.17)
(6.17)
Передаточная функция фильтра  представляет собой дробно-рациональную функцию с вещественными коэффициентами, то есть отношение полиномов
представляет собой дробно-рациональную функцию с вещественными коэффициентами, то есть отношение полиномов
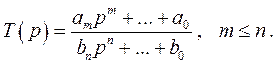 (6.18)
(6.18)
Корни числителя и знаменателя могут быть вещественными или комплексно-сопряженными, причем корни полинома знаменателя должны лежать в левой комплексной полуплоскости параметра p (иначе это будет не усилитель фильтра, а генератор). Такие полиномы называются полиномами Гурвица.
ФНЧ в общем виде описывается передаточной функцией
 (6.19)
(6.19)
В справочниках приводятся различные варианты передаточных функций T(p) ФНЧ или полиномов знаменателя (6.19), различающиеся коэффициентами и характером АЧХ-фильтров. Известны полиномы (и соответственно фильтры) Баттерворта, Чебышева, Бесселя, Лежандра, Кауэра-Золотарёва и другие.
Передаточные функции T(p) для ФВЧ, ПФ и других типов фильтров рассчитываются из передаточных функций ФНЧ – фильтров-прототипов.
Если полученный на этапе аппроксимации полином имеет порядок выше второго, то такой полином нужно разложить на произведение полиномов 2-го порядка.
| На рис. 6.29 дана АЧХ ФНЧ типа Баттерворта. Для него характерна «плоская» характе-ристика в полосе пропускания, на частоте f П δ = 3 дБ. Наклон АЧХ выше частоты f П пологий (в сравнении с ФНЧ других типов). | 
|
| На рис. 6.30 дана АЧХ ФНЧ типа Чебышева. Для него характерна «волнистая» характеристика в полосе пропускания, минимальное затухание δ на частоте f П может иметь любую заданную величину. Наклон АЧХ более крутой, чем у ФНЧ Баттерворта. | 
|
| На рис. 6.31 дана АЧХ ФНЧ типа Кауэра-Золотарёва (в иностранных источниках – эллиптический). Для него характерна «волнистая» характеристика в полосе пропускания и в полосе затухания. Наклон АЧХ наиболее крутой, в сравненинии с ФНЧ Баттерворта и Чебышева. | 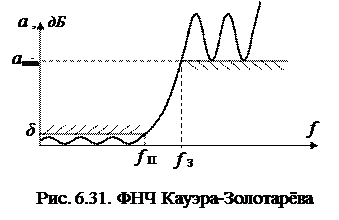
|
6.4.3 Типы звеньев фильтров второго порядка
Передаточная функция фильтра  высокого порядка может быть представлена в виде произведения передаточных функций 2-го порядка:
высокого порядка может быть представлена в виде произведения передаточных функций 2-го порядка:
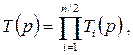
где 
 (6.20)
(6.20)
 Пусть имеется набор некоторых устройств с RВЫХ =0 (рис. 6.32). В этом случае подключение каждого следующего устройства не сказывается на АЧХ предыдущих устройств.
Пусть имеется набор некоторых устройств с RВЫХ =0 (рис. 6.32). В этом случае подключение каждого следующего устройства не сказывается на АЧХ предыдущих устройств.
Передаточная функция звена 2-го порядка

где ωР – частота полюса;
ωZ – частота нуля;
QР –добротность полюса;
QZ –добротность нуля.
Звено 2-го порядка ФНЧ
 (6.21)
(6.21)
где  - частота звена (дпя ФНЧ – частота среза);
- частота звена (дпя ФНЧ – частота среза);
QН – добротность звена;
 - коэффициент передачи.
- коэффициент передачи.
Звено 2-го порядка ПФ
 (6.22)
(6.22)
Звено 2-го порядка ФВЧ
 (6.23)
(6.23)
Звено 2-го порядка фильтра с нулём передачи:
 (6.24)
(6.24)
Удобно рассматривать характеристики фильтров при нормированной оси частот Ω = (f / fСР).
Примеры полиномов звеньев фильтров 2-го порядка:
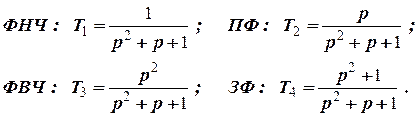
 АЧХ этих звеньев приведены на рис. 6.33. У фильтров НЧ и ВЧ 2-го порядка крутизна спада АЧХ равна 40 дБ/дек, у ПФ 2-го порядка крутизна спада каждой ветви равна 20 дБ/дек.
АЧХ этих звеньев приведены на рис. 6.33. У фильтров НЧ и ВЧ 2-го порядка крутизна спада АЧХ равна 40 дБ/дек, у ПФ 2-го порядка крутизна спада каждой ветви равна 20 дБ/дек.
6.4.4. Реализация звеньев фильтров второго порядка на основе ОУ
Первоначально электрические фильтры строились исключительно на пассивных элементах – катушках индуктивности L и конденсаторах С. Недостатки таких LС-фильтров – большие габариты и масса, высокая трудоёмкость изготовления и настройки, невозможность миниатюризации – вызваны применением катушек индуктивности L.
Использование ОУ позволяет строить звенья активных фильтров на резисторах R и конденсаторах С и полностью отказаться от катушек индуктивности.
Звенья активных RС фильтров (АRС-фильтров) имеют RВЫХ ≈ 0, что позволяет включать их последовательно (рис. 6.32) для получения фильтров требуемого порядка.
В [6] предложена классификация схем звеньев АRС-фильтров в зависимости от добротности Q звена:
· низкодобротные, Q ≤ 2;
· среднедобротные, Q ≤ 20;
· высокодобротные, Q >20.
Рассмотрим некоторые схемы АRС схем ФНЧ.
В результате выполненной аппроксимации для конкретного i-го звена имеем передаточную функцию 2-го порядка (6.19)
 (а)
(а)
· Схема низкодобротного звена ФНЧ 2-го порядка (одна из возможных реализаций) приведена на рис. 6.34.

Рис. 6.34. Низкодобротное звено ФНЧ 2-го порядка
Порядок АRС звена определяется числом конденсаторов. Схема выполнена на ОУ, включённом по схеме единичного усиления.
В [6] приведены формулы, позволяющие рассчитать значения резисторов и конденсаторов данной схемы:
 (б)
(б)
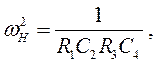 (в)
(в)
 (г)
(г)
 (д)
(д)
где K должно быть меньше единицы.
Имеем систему из 4 уравнений (из выражения (а) берём коэффициенты K , ωН , QН ) и 6 неизвестных. Такая система имеет много решений. Для решения системы уравнений (б ÷ д) нужно ввести дополнительные условия. Возможно, что при этом система уравнений не будет иметь решения; тогда нужно будет ввести другие дополнительные условия.
Пример
Дано:  fН = fП = 10 кГц = 104 .
fН = fП = 10 кГц = 104 .
Из выражения для T(p) следует: ωН = 1, QН =1, Ki =0,5.
Пусть С2 = С4 = С, R1 =1 (этим мы исключаем 2 неизвестных, чтобы число неизвестных равнялось числу уравнений).
Подставим в (г):

Уравнение не решается!
Введём другое предположение:
Пусть R1 =1, R3 =1. Тогда:
Из (в): С2С4 = 1.
Из (г): 

Из (д): 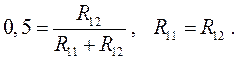
Из (б): 
Таким образом, в условных (нормированных) единицах имеем:
R1 =1, R11 = R12 =2, R3 =1, С2 =2, С4 =0,5.
Теперь проведём денормирование. Зададим RД – сопротивление денормирования. Пусть RД = 1 кОм = 103 .
Тогда R1 =1 кОм, R11 = R12 =2 кОм, R3 =1 кОм.
Денормирование конденсаторов проводится по формуле
 (6.25)
(6.25)
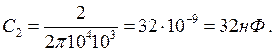

На рис. 6.35 приведена АЧХ рассчитанного звена ФНЧ. В полосе пропускания К = – 6дБ = 0,5; после fП = 10 кГц идёт спад АЧХ с крутизной 12 дБ/окт (40дБ/дек).
 |
· Схема среднедобротного звена ФНЧ 2-го порядка (2< Q ≤ 20) дана на рис. 6.36. Нормированные значения компонентов можно найти из четырёх уравнений [6]:



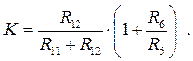

Рис. 6.36. Среднедобротное звено ФНЧ 2-го порядка
В этой схеме коэффициент K может быть как меньше, так и больше единицы. Введя подстроечные элементы R5 , R6 , то есть усложнив предыдущую схему, мы получили схему с меньшей чувствительностью к изменению параметров.
· Схема высокодобротного звена ФНЧ 2-го порядка дана на рис. 6.37.

Рис. 6.37. Высокодобротное звено ФНЧ 2-го порядка
Нормированные значения компонентов можно найти из уравнений [6]:

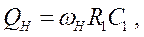

· В справочниках приводятся АRС-звенья 2-го и 1-го порядка для ПФ, ФВЧ и других типов звеньев. Многие типы АRС-фильтров и их звеньев включены в библиотеки современных программ компьютерного моделирования [7].
6.4.5. Понятие о фильтрах на коммутируемых конденсаторах
АRС фильтры целесообразно выполнять в виде интегральных микросхем (ИМС). Но при этом нужно учитывать, что в ИМС можно реализовать конденсаторы ёмкостью от единиц пикофарад до нескольких нанофарад, а резисторы – сопротивлением от единиц ом до нескольких килоом (определяется технологическим процессом изготовления ИМС). В то же время, особенно на низких частотах, в схемах АRС-фильтров требуются большие номиналы R или С.
Рассмотрим для примера схему ФНЧ первого порядка (рис. 6.38).
|
| ||||||
| Рис. 6.38. Звено АRС ФНЧ 1-го порядка: а - схема звена; б - передаточная функция |
Пусть fН = 50 Гц; ωН = 2πּ50;

Тогда а1 =1; К= - 1, R1 = R2 ;

Зададим СФ = 100 пФ = 10-10.
Тогда: R1 = R2 = 1/(2πּ50ּ10-10) = 31,83ּ10-10 = 31,83 МОм.
Резисторы со столь большим сопротивлением в ИМС невозможно изготовить.
Зададим R1 = R2 = 1 кОм = 103.
Тогда: СФ = 1/(2πּ50ּ103) = 3,183ּ103 = 3,183 мкФ.
Конденсаторы с такой большой ёмкостью в ИМС также невозможно изготовить.
В виде навесных элементов можно применить резисторы и конденсаторы с большими значениями R и С, но невозможно обеспечить их требуемую точность и стабильность. Так, резисторы с сопротивлением более 1 Мом не обеспечивают требуемую точность и стабильность из-за сравнимого по величине и непостоянного сопротивления утечки.
Идею построения схемы на коммутируемых конденсаторах рассмотрим на примере (рис. 6.39,а).
На рис. 6.39,б изображены 2 противофазных последовательности импульсных сигналов φ1 и φ2 , следующих с частотой fC.
τC = 1/2fC . (6.26)
|
| ||||||
| Рис. 6.39. Звено схемы на коммутируемых конденсаторах: а - коммутируемый конденсатор; б) временные диаграммы |
Во время такта φ1 (длительность такта τC) ключи К1-1, К1-2 замкнуты, ключи К2-1, К2-2 разомкнуты, конденсатор С (рис. 6.37,а) заряжается и накапливает заряд Q. Во время такта φ2 (длительность такта также τC) ключи К1-1, К1-2 разомкнуты, ключи К2-1, К2-2 замкнуты, конденсатор С разряжается.
Q = С∙(U1 – U 2). (6.27)
Ток заряда равен
 (6.28)
(6.28)
Средний ток, протекающий через конденсатор С за период fС с учётом (6.23), равен
 (6.29)
(6.29)
Из выражения (6.26) следует, что множитель перед разностью напряжений является эквивалентом проводимости некого RЭ:
RЭ = 1/СfС . (6.30)
Необходимое условие: частота fС должна быть намного выше максимальной частоты входного сигнала fВ , чтобы за время такта τC входной сигнал U1 практически не изменился.
Пусть С = 10 пФ = 10-11 , fС = 10 кГц. Тогда RЭ = 1/СfС = 107 = 10 МОм.
Таким образом, в схеме звена фильтра (рис. 6.39,а) высокоомные резисторы R1 и R2 могут быть заменены на эквивалентные им коммутируемые конденсаторы по схеме рис. 6.39,а. Схема звена ФНЧ на коммутируемых конденсаторах приведена на рис. 6.40.

Передаточная функция этого фильтра, соответствующая прототипу (рис.6.38,б), равна:
 (6.31)
(6.31)
Из выражения (6.31) следует, что на точность реализации передаточной функции влияет не точность значений ёмкостей и их стабильность, а их отношение. Технологически достижима точность отношений значений ёмкостей порядка 0,1%.
Таким образом, фильтры на коммутируемых конденсаторах могут быть выполнены полностью на полупроводниковых ИМС.
|
из
5.00
|
Обсуждение в статье: Активные RC-фильтры на основе ОУ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы






