 |
Главная |
Система частотной автоподстройки (ЧАПЧ)
|
из
5.00
|
Проведём анализ работы линейной системы ЧАПЧ, для чего конкретизируем схему (рис. 11.1) – будем считать, что в какой-то момент времени произошло скачкообразное изменение на величину ΔfГ частоты сигнала ГУН относительно частоты fОП либо частоты fОП относительно частоты fГ. В обоих случаях частота fГ будет отличаться от частоты fОП на величину ΔfГ.
На рис. 11.2 этот эффект моделируется тем, что на выходе ГУН (через сумматор) вводится возмущающий сигнал Δf .
Анализ будем проводить в p-области, то есть для преобразованных по Лапласу переменных. Коэффициенты передачи отдельных узлов системы представлены на рис. 11.2. Как во всякой линейной системе, коэффициенты передачи определяются как отношение приращений сигналов на выходе и входе. Поэтому





В результате реакции системы АПЧ на скачок частоты Δf частота fГ сигнала на выходе ГУН будет отличаться от частоты fОП на величину ΔfОСТ (р). Найдём эту величину, для чего составим уравнение непрерывности так же, как это делалось при анализе системы с обратной связью:
ΔfОСТ (р) = Δf(р) + ΔfОСТ (р) ·К1(р) ·К2(р) ·К3(р) ·К4(р) , (11.1)
где Δf(р) = Δf / р) - изображение скачка Хэвисайда Δf .
Из (1) получим выражение
 (11.2)
(11.2)
Рассмотрим самый простой случай, когда коэффициенты передачи всех устройств, за исключением ФНЧ, являются частотно-независимыми: К1(р) = = SЧД – крутизна преобразования частотного детектора, К3(р) = КУС , К4(р) = = SГУН – крутизна преобразования ГУН; ФНЧ представим моделью RC-филь-тра первого порядка с передаточной функцией  , где τ = RC – постоянная времени RC-цепи.
, где τ = RC – постоянная времени RC-цепи.
С учётом принятых допущений выражение (10.2) записывается в виде:
 (11.3)
(11.3)
Для того, чтобы система АПЧ была устойчива, то есть не входила в режим генерации, необходимо и достаточно, чтобы коэффициенты полинома знаменателя относительно переменной p были положительны. Коэффициент τ = RC при первой степени всегда положительны. Положительность свободного члена обеспечивается условием 1– SЧД·КУС ·SГУН > 0, откуда следует условие SЧД·КУС ·SГУН < 0.
Оно выполняется, если один из коэффициентов передачи в произведении трёх членов по знаку противоположен двум остальным. Это условие легко обеспечивается выбором знака коэффициента передачи усилителя на основе ОУ.
Перейдём в (11.3) к оригиналу и найдём, чему равна погрешность подстройки частоты ГУН к изменившейся частоте опорного сигнала через достаточно большой промежуток времени. Для этого воспользуемся свойством преобразования по Лапласу: если F(p) есть преобразование F(t), то 
На основании выражения (10.3) получим формулу
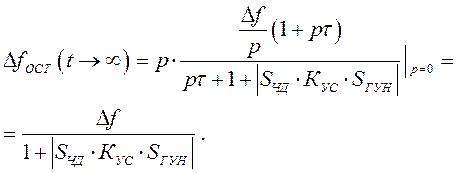 (11.4)
(11.4)
Из (11.4) следует, что в системе с ЧАПЧ всегда существует остаточная погрешность подстройки. Она может быть сделана достаточно малой по сравнению с исходным скачком частоты при реализации большого значения коэффициента по петле ОС  .
.
|
из
5.00
|
Обсуждение в статье: Система частотной автоподстройки (ЧАПЧ) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

