 |
Главная |
Понятие функции нескольких переменных
|
из
5.00
|
V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Понятие функции нескольких переменных
Ранее была рассмотрена функция одной независимой переменной. Однако, решая конкретные практические задачи, исследователь, в общем случае, сталкивается с такими явлениями, которые зависят сразу от нескольких независимых переменных величин. В качестве самых простых примеров этого можно привести необходимость вычисления площади прямоугольника либо объема параллелепипеда. Действительно, площадь прямоугольника определяется двумя независимыми друг от друга величинами – длинами сторон прямоугольника  и
и  :
:
 .
.
Объем параллелепипеда определяется уже тремя независимыми величинами – длинами его ребер  ,
,  ,
,  :
:
 .
.
Можно привести и более сложные примеры. Иначе говоря, число независимых переменных величин может быть каким угодно. В этих случаях говорят, что искомая величина является функцией двух, трех или большего числа переменных.
Часто пытаются исключить второстепенные переменные и оставить только одну, основную, то есть пытаются получить функцию одной переменной. Но это не всегда возможно. Упрощение выражения дает часто функцию двух или трех переменных. Сразу же необходимо отметить, что исследование функций многих переменных имеет подобные методы. Поэтому для простоты будем изучать функции двух переменных и полученные результаты при необходимости обобщать затем на произвольный случай.
В случае одной переменной функция являлась оператором, который каждому элементу из множества  ставил в соответствие один и только один элемент из множества
ставил в соответствие один и только один элемент из множества  .
.
Каким же образом определяется аргумент функции двух переменных? Так как мы исследуем функции действительных аргументов, то величина такой функции зависит от пары двух действительных чисел. С точки зрения теории множеств это не что иное, как произведение двух множеств  и
и  , к которым принадлежат переменные
, к которым принадлежат переменные  и
и  .
.
Определение 5.1.1. Пусть  , а
, а  , тогда произведение
, тогда произведение  дает новое множество
дает новое множество  , каждый элемент которого содержит пару чисел
, каждый элемент которого содержит пару чисел  .
.
Из определения 5.1.1 следует, что, зная множество значений  и
и  функции двух переменных, можно найти область ее определения. Очевидно, это будут все возможные комбинации
функции двух переменных, можно найти область ее определения. Очевидно, это будут все возможные комбинации  и
и  .
.
Произведение двух действительных числовых множеств  и
и  образует множество в пространстве
образует множество в пространстве  . Графическое представление этого произведения – это плоскость или часть этой плоскости.
. Графическое представление этого произведения – это плоскость или часть этой плоскости.
Определение 5.1.2. Функцией двух переменных называется соотношение, которое каждой паре чисел  ставит в соответствие одно и только одно число
ставит в соответствие одно и только одно число  .
.
Если имеется функция  переменных, то ее областью определения будет пространство
переменных, то ее областью определения будет пространство 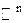 или его часть. Такое множество уже графически не представимо.
или его часть. Такое множество уже графически не представимо.
Функции двух переменных, так же как и функции одной переменной, можно представить с помощью таблицы, графика или аналитического выражения. Табличный способ наименее удобен, однако, при экспериментальном определении значения функции он может оказаться единственным. Более информативны графическое и аналитическое задание функции. При этом последний способ наиболее удобен, так как дает возможность провести полное исследование данного понятия.
Для графического представления функции двух переменных рисуют трехмерную систему координат, например, прямоугольную декартовую. На плоскости  изображают область определения
изображают область определения  данной функции. В каждой точке области определения восстанавливается перпендикуляр, который имеет длину, равную значению функции в этой точке. Объединяя все полученные точки, получают некоторую поверхность (рис. 5.1.1). Таким образом, графически функция двух переменных – это некоторая поверхность. Для изображения функций большего числа переменных графический способ уже не применим.
данной функции. В каждой точке области определения восстанавливается перпендикуляр, который имеет длину, равную значению функции в этой точке. Объединяя все полученные точки, получают некоторую поверхность (рис. 5.1.1). Таким образом, графически функция двух переменных – это некоторая поверхность. Для изображения функций большего числа переменных графический способ уже не применим.

Рис. 5.1.1
При аналитическом задании функции двух переменных записывается формула  , при помощи которой по заданным значениям независимых переменных отыскивается значение функции. Увеличение числа переменных при аналитическом задании функции проблем не создает (
, при помощи которой по заданным значениям независимых переменных отыскивается значение функции. Увеличение числа переменных при аналитическом задании функции проблем не создает (  ).
).
При исследовании функции двух или нескольких переменных возникают те же понятия, что и для функции одной переменной: предел, непрерывность, приращения, производная.
Рассмотрим вначале сечения поверхности  плоскостями
плоскостями  и
и  (рис. 5.1.2).
(рис. 5.1.2).
Так как на линии  константой является
константой является  , то на ней
, то на ней  меняется лишь в зависимости от изменения
меняется лишь в зависимости от изменения  . Если в точке
. Если в точке  задать приращение
задать приращение  , то произойдет перемещение в точку
, то произойдет перемещение в точку  . Разность аппликат
. Разность аппликат  в этих точках будет равна изменению значения функции
в этих точках будет равна изменению значения функции  , которое не будет зависеть от переменной
, которое не будет зависеть от переменной  .
.

Рис. 5.1.2
Таким образом, давая приращение 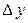 , получаем приращение
, получаем приращение  , которое называется частным приращением
, которое называется частным приращением  по
по  и обозначается
и обозначается  .
.
Аналогично определяется частное приращение  по
по  :
:  .
.
Давая одновременно приращения переменным  и
и  , получаем полное приращение функции:
, получаем полное приращение функции:  . При этом необходимо иметь в виду, что
. При этом необходимо иметь в виду, что  .
.
Введем теперь понятие окрестности точки на плоскости.
Определение 5.1.3.  -окрестностью точки
-окрестностью точки  с радиусом
с радиусом  называется множество всех точек
называется множество всех точек  , которые удовлетворяют неравенству
, которые удовлетворяют неравенству  , или, иначе говоря, множество всех точек, которые лежат внутри круга радиуса
, или, иначе говоря, множество всех точек, которые лежат внутри круга радиуса  с центром в точке
с центром в точке  (рис. 5.1.3).
(рис. 5.1.3).

Рис. 5.1.3
На основании определения  -окрестности можно ввести понятие предела функции двух переменных. Пусть функция
-окрестности можно ввести понятие предела функции двух переменных. Пусть функция  определена в некоторой области
определена в некоторой области  (рис. 5.1.3). Возьмем в этой области некоторую точку
(рис. 5.1.3). Возьмем в этой области некоторую точку  .
.
Определение 5.1.4. Число  называется пределом функции
называется пределом функции  при
при  стремящемся к
стремящемся к  , если для любого
, если для любого  существует такое
существует такое 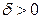 , что для любого
, что для любого  справедливо
справедливо  .
.
Определение 5.1.5. Пусть точка  принадлежит области определения функции, тогда
принадлежит области определения функции, тогда  называется непрерывной в этой точке, если
называется непрерывной в этой точке, если  при любом стремлении точки
при любом стремлении точки  к точке
к точке  .
.
Приведенное в определении 5.1.5 равенство можно записать несколько иначе:
 ,
,
 или
или  .
.
Следовательно, в окрестности точки непрерывности функции ее полное приращение стремится к нулю при стремлении к данной точке.
Определение 5.1.6. Функция двух переменных называется непрерывной в некоторой области, если она непрерывна в каждой точке этой области.
Если в какой-то точке  не выполняются условия непрерывности, то говорят, что это точка разрыва функции. Существуют следующие случаи:
не выполняются условия непрерывности, то говорят, что это точка разрыва функции. Существуют следующие случаи:
1)  определена во всех точках, кроме
определена во всех точках, кроме  ;
;
2)  определена во всех точках, но не существует предел
определена во всех точках, но не существует предел  ;
;
3)  определена во всех точках, но
определена во всех точках, но  .
.
|
из
5.00
|
Обсуждение в статье: Понятие функции нескольких переменных |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

