 |
Главная |
Решение системы линейных уравнений (61-70)
|
из
5.00
|
А. Метод Гаусса.
Пример.Решить методом Гаусса систему уравнений

Используя первое уравнение, исключим вначале  из второго и третьего уравнений. Для этого сложим первое уравнение, умноженное на -1, со вторым, умноженным на 2. Затем первое уравнение, умноженное на -2, сложим с третьим уравнением.
из второго и третьего уравнений. Для этого сложим первое уравнение, умноженное на -1, со вторым, умноженным на 2. Затем первое уравнение, умноженное на -2, сложим с третьим уравнением.
Получим

Исключим из третьего уравнения 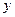 , складывая второе уравнение, умноженное на 27, с третьим, умноженным на 13:
, складывая второе уравнение, умноженное на 27, с третьим, умноженным на 13:
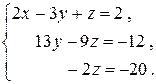
Теперь последовательно находим  и
и  :
:

 ,
,  ,
,  ;
;
 ,
,  ,
,  .
.
Ответ:  ,
,  ,
,  .
.
Б. Матричный способ.
Рассмотрим вначале действия над матрицами.
Матрицей размером  называется таблица чисел, содержащая
называется таблица чисел, содержащая  строк и
строк и 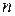 столбцов.
столбцов.
Если  , то получаем квадратную матрицу
, то получаем квадратную матрицу  го порядка.
го порядка.
При умножении матриц каждая строка первой матрицы умножается на каждый столбец второй.
При умножении строки на столбец перемножаются их первые элементы, вторые и т.д. и результаты складываются. Поэтому можно умножать только такие матрицы, у которых число столбцов первой матрицы равно числу строк второй.
Примеры.

 ,
,
 .
.
Матрица  называется обратной по отношению к квадратной матрице
называется обратной по отношению к квадратной матрице  , если
, если
 .
.
Покажем, как найти обратную матрицу  .
.
Пусть
 .
.
а)  .
.
Так как  , то
, то  существует.
существует.
б) Пусть 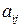 - элемент матрицы
- элемент матрицы  , расположенной в
, расположенной в  -й строке и
-й строке и  -м столбце. Если в определителе
-м столбце. Если в определителе  вычеркнуть строку и столбец с элементом
вычеркнуть строку и столбец с элементом 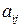 , то получим дополнительный минор
, то получим дополнительный минор  элемента
элемента 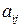 . Это определитель 2-го порядка.
. Это определитель 2-го порядка.
Составим матрицу  из дополнительных миноров
из дополнительных миноров  элементов матрицы
элементов матрицы  :
:
 .
.
в) Составим матрицу  из алгебраических дополнений
из алгебраических дополнений  элементов
элементов  .
.
|
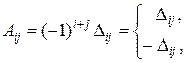
 .
.
г) Транспонируем матрицу  , т.е. строки поменяем местами со столбцами:
, т.е. строки поменяем местами со столбцами:
 .
.
Обратная матрица  определяется формулой
определяется формулой
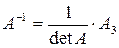 ,
,
 .
.
Покажем, как решается система уравнений матричным способом.
Пример. Решить систему 
Решение.Обозначим:
 ,
,  ,
,  .
.
Получаем матричное уравнение  .
.
Его решение 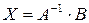 , т.е.
, т.е.
 .
.
Ответ: 
Собственные значения и собственные векторы линейного преобразования (71-80)
Пусть
 ,
, 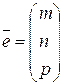 .
.
Ненулевой вектор  называется собственным вектором линейного преобразования, заданного матрицей А, если
называется собственным вектором линейного преобразования, заданного матрицей А, если
 ,
,
где  – собственное значение, находящееся из характеристического уравнения
– собственное значение, находящееся из характеристического уравнения
 ,
,
или
 .
.
Раскрываем определитель по элементам первой строки:
 ,
,
 ,
, 
 , т.к.
, т.к.  ;
;  .
.
Составим систему уравнений для координат  собственного вектора
собственного вектора  . Коэффициентами при неизвестных будут элементы определителя при
. Коэффициентами при неизвестных будут элементы определителя при  :
:



Полагаем  , тогда
, тогда  ,
,  .
.
 2 собственный вектор с собственным значением
2 собственный вектор с собственным значением  .
.
|
из
5.00
|
Обсуждение в статье: Решение системы линейных уравнений (61-70) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


 2 четное число,
если
2 четное число,
если