Внутренние силовые факторы при изгибе

Пример 1. Рассмотрим балку, на которую действует пара сил с моментом т и внешняя силаF(рис. 29.3а). Для определения внут­ренних силовых факторов пользуемся методом сечений.

 

Рассмотрим равновесие участка 1 (рис. 29.36).

Под действием внешней пары сил участок стремится развер­нуться по часовой стрелке. Силы упругости, возникающие в сече­нии 1, удерживают участок в равновесии.

Продольные силы упругости выше оси бруса направлены напра­во, а силы ниже оси направлены налево. Таким образом, при равно­весии участка 1 получим: F_z = 0. Продольная сила N в сечении равна нулю. Момент сил упругости относительно оси Ох может быть получен, если суммировать элементарные моменты сил упругости в сечении 1-1 относительно оси Ох:

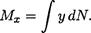
Из схемы вала на рис. 29.3 б видно, что часть волокон (выше оси) испытывают сжатие, а волокна ниже оси растянуты. Следовательно, в сечении должен существовать слой не растянутый и не сжатый, где напряжения σ равны нулю.

Такой слой называют нейтральным слоем (НС). Линия пересе­чения нейтрального слоя с плоскостью поперечного сечения бруса называют нейтральной осью.

Нейтральный слой проходит через центр тяжести сечения. Здесь нейтральный слой совпадает с осью Ох.

Практически величина изгибающего момента в сечении опреде­ляется из уравнения равновесия: Σ т_Х1^_₁ = m — М_Х1 = 0; М_Х1 = т.

Таким образом, в сечении1-1 продольная сила равна нулю, из­гибающий момент в сечении постоянен.

Изгиб, при котором в поперечном сечении бруса возникает толь­ко изгибающий момент, называется чистым изгибом.

Рассмотрим равновесие участка бруса от свободного конца до сечения 2 (рис. 29.Зв).

Запишем уравнения равновесия для участка бруса:

 

В сечении бруса 2-2 действует поперечная сила, вызывающая сдвиг.

Изгибающий момент в сечении:

z₂ — расстояние от сечения 2 до начала координат.

Изгибающий момент зависит от расстояния сечения до начала координат.

Изгиб, при котором в поперечном сечении бруса возникает изги­бающий момент и поперечная сила, называется поперечным изгибом.

Принятые в машиностроении знаки поперечных сил и изгибающих моментов

Знаки поперечных сил

Поперечная сила в сече­нии считается положительной, если она стремится развер­нуть сечение по часовой стрелке (рис. 29.4а), если против, — отрицательной (рис. 29.4б).

Знаки изгибающих моментов

Если действующие на участке внешние силы стремятся изогнуть бал­ку выпуклостью вниз, то изгибающий момент считается положительным (рис. 29.5а), если наоборот — отрица­тельным (рис. 29.5б).

 

Выводы

При чистом изгибе в поперечном сечении балки возникает только изгибающий момент, постоянный по величине.

При поперечном изгибе в сечении возникает изгибающий мо­мент и поперечная сила.

Изгибающий момент в произвольном сечении балки численно равен алгебраической сумме моментов всех внешних сил, прило­женных к отсеченной части, относительно рассматриваемого се­чения.

Поперечная сила в произвольном сечении балки численно равна алгебраической сумме проекций всех внешних сил, действующих на отсеченной части, на соответствующую ось.

Пример 2. На балку действует пара сил с моментом т и рас­пределенная нагрузка интенсивностью q. Балка защемлена справа

 

Рассечем балку на участке 1 на расстоянии z₁ от левого края. Рассмотрим равновесие отсеченной части. Из уравнения

получим:

 

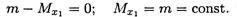
Участок 1 — участок чистого изгиба.

Рассечем балку на участке 2 на расстоянии z₂ > а от края, z₂ — расстояние сечения от начала координат.

Из уравнения ΣFy ⁼ 0 найдем поперечную силу Q_2. Заменя­ем распределенную нагрузку на рассматриваемом участке равнодей­ствующей силой q(z₂ — а).

Из уравнения моментов определяем изгибающий момент в сече­нии:

На втором участке возникает поперечный изгиб.

Выводы

При действии распределенной нагрузки возникает поперечная сила, линейно зависящая от координаты сечения.

Изгибающий момент на участке с распределенной нагрузкой меняется в зависимости от координаты сечения по параболическо­му закону.