 |
Главная |
Расчёты на жесткость при изгибе
|
из
5.00
|
Пример 6. Определить прогиб двутавровой балки № 30 (ГОСТ 8239—72) пролетом l = 6 м, нагруженной равномерно распределенной по всему пролету нагрузкой интенсивностью q = 20 Н/мм.
Решение
Абсолютная величина прогиба определяется по формуле:
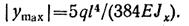
Принимая Е = 2,0*105 Н/мм2 и Jx = 7080*104 мм4 (по таблице ГОСТ)., получаем

что составляет 1/251 пролета

Пример 7. Подобрать сечение стальной двутавровой балки пролетом 4,8 м, нагруженной равномерно распределенной по всему пролету нагрузкой интенсивностью q = 5 кНм = 5 Н/мм и сосредоточенной силой Р = 30 кН, приложенной посередине пролета, исходя из условий прочности и жесткости, если допускаемое напряжение [σ] = 140 Н/мм2, а допускаемый прогиб [f/l] = 1/600. Принять E = 2,1 • 105 Н/мм2.
Решение
Наибольший изгибающий момент при заданном нагружении

Требуемый момент сопротивления по условию прочности

Ближайший по ГОСТ 8239—72 двутавр № 24 имеет Wx = 289 см3.
Абсолютная величина наибольшего прогиба посередине пролета определяется как сумма прогибов для каждого из двух нагружений:

По условию жесткости он не должен превышать 1/600 пролета. Имеем

Сократив на l и подставив числовые значения, получим

откуда требуемый момент инерции сечения

Двутавр № 24 имеет J = 3460 см4 и недостаточен для обеспечения жесткости балки. Следует принять двутавр № 30 с Jx = 7080 см4.
Пример 8. Проверить жесткость балки, изображенной на рис. 2.63, если угол поворота ее свободного конца не должен превышать 1°; принять Е = 2,0*104 Н/мм2.
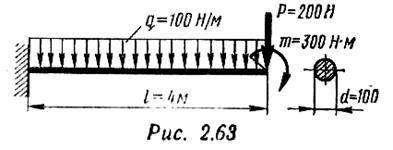
Решение
Момент инерции заданного сечения балки

Полный угол поворота свободного конца В определится как сумма углов поворота от каждой из трех нагрузок, при этом учтем, что 100 Н/м=0,1 Н/мм:

Жесткость балки недостаточна.
Расчёты на косой изгиб
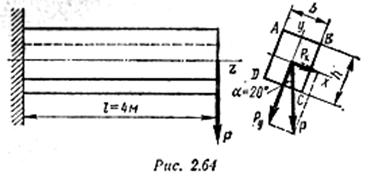 Пример 9. Деревянная балка прямоугольного сечения с отношением сторон b/h = 1/2 (рис. 2.64) защемлена одним концом и изгибается силой Р = 1,5 кН, приложенной на свободном конце. Определить требуемые размеры сечения, если допускаемое напряжение [σ] = 11 Н/мм2.
Пример 9. Деревянная балка прямоугольного сечения с отношением сторон b/h = 1/2 (рис. 2.64) защемлена одним концом и изгибается силой Р = 1,5 кН, приложенной на свободном конце. Определить требуемые размеры сечения, если допускаемое напряжение [σ] = 11 Н/мм2.
Решение
Разложим силу Р на составляющие по направлениям главных центральных осей сечения:

Наибольшие изгибающие моменты от каждой из составляющих сил возникнут в защемленном сечении:

Наибольшие напряжения будут в точках А и С; в точке А — растягивающие, в точке С — сжимающие. По абсолютному значению они равны.
Составим условие прочности для точки А, учитывая, что Wx = bh2/6, a Wy = hb2/6:

Подставим числовые значения:

Откуда

и, следовательно,
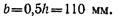
Пример 10. Определить необходимый по условию прочности диаметр поперечного сечения стержня, изгибаемого силами, действующими в двух взаимно перпендикулярных плоскостях (рис. 2.65, а). Допускаемое напряжение [σ] =130 Н/мм2.
Решение
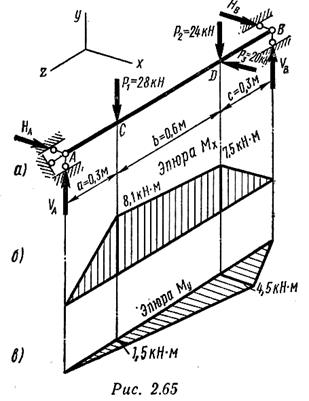 Определим опорные реакции от вертикальной
Определим опорные реакции от вертикальной
нагрузки:

откуда

Составляем проверочное уравнение:
 |
Так как уравнение ΣMBв = 0 удовлетворяется тождественно, то вертикальные реакции вычислены верно.
Составим уравнения равновесия в горизонтальной плоскости:


Откуда

Составляем проверочное уравнение:
Уравнение обращается в тождество, значит реакции найдены верно.
На рис. 2.65, б, в построены эпюры изгибающих моментов соответственно в вертикальной Мх и горизонтальной Му плоскостях. Определяем ординаты этих эпюр для характерных сечений:

Результирующие изгибающие моменты в сечениях С и D составят:

Опасным оказалось сечение D: в нем возникает наибольший изгибающий момент. Составим для этого сечения условие прочности:

Откуда

Или

Принимаем d = 90 мм.
Пример 11. Ступенчатая стальная полоса толщиной δ = 24 мм (рис. 2.66) поддерживает груз Р. Определить допускаемую величину силы Р по условию прочности полосы, если допускаемое напряжение для нее [σ] =160 Н/мм2.
 Решение
Решение
Нижняя ступень полосы нагружена центрально. Условие прочности для любого сечения этой ступени имеет вид:

Откуда

Верхняя ступень полосы испытывает внецентренное растяжение. Эксцентриситет приложения растягивающей силы Р (см. рис. 2.66)

Условие прочности для любого сечения верхней ступени полосы имеет вид:

откуда

Очевидно, из двух найденных значений допускаемой величины силы Р следует принять меньшее, определяемое прочностью верхней ступени:

Приведенный пример показывает, что не всегда увеличение сечения сопровождается возрастанием допускаемой нагрузки. В данном случае как раз наоборот: вследствие появления эксцентриситета прочность верхней ступени полосы с большей площадью сечения меньше, чем нижней ее ступени.
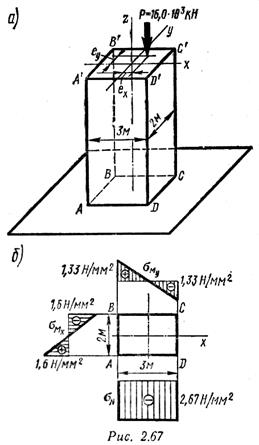 Пример 12. Каменный столб нагружен силой Р = 16,0*103 кН (рис. 2.67, а). Определить, не учитывая массы столба, наибольшее и наименьшее сжимающие напряжения в его подошве и указать точки, где они возникают.
Пример 12. Каменный столб нагружен силой Р = 16,0*103 кН (рис. 2.67, а). Определить, не учитывая массы столба, наибольшее и наименьшее сжимающие напряжения в его подошве и указать точки, где они возникают.
Решение
Сила Р приложена с эксцентриситетом, величина которого определяется его составляющими вдоль оси х: ех = 0,25 м и вдоль оси у: еу = 0,2 м. От внецентреннего приложения силы возникает косой изгиб, составляющие изгибающего момента относительно осей х и у соответственно равны:

Наибольшее по абсолютному значению напряжение возникает в точках ребра СС'; здесь всем внутренним силовым факторам N = — Р, Мх и Му соответствует возникновение сжимающих напряжений; наименьшее по абсолютному значению напряжение будет в точках ребра АA', там моментам Мх и Му соответствуют растягивающие напряжения, а продольной силе N = -- P — сжимающие.
Для определения напряжения в угловых точках сечения воспользуемся формулой
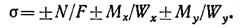
Вычисляем моменты сопротивления:

Подставляя числовые значения, выраженные в кН и м, в формулу нормальных напряжений σ, получаем:
для точки С

для точки А

При заданном эксцентриситете силы в точке А возникают растягивающие напряжения.
На рис. 2.67, б построены все три составляющие эпюры нормальных напряжений в поперечном сечении столба, соответствующие внутренним силовым факторам N, Мх, Му.
Контрольные вопросы и задания
1. Какие внутренние силовые факторы возникают в сечении балки при чистом и поперечном изгибах?
2. Почему при поперечном изгибе в продольных сечениях балки возникают касательные напряжения?
3. Каким опытом можно подтвердить возникновение касательных напряжений в продольных сечениях балки?
4. В какой точке поперечного сечения (рис. 33.8) касательные напряжения при поперечном изгибе максимальны?
 Варианты ответов: 1. А. 2. В. 3. С. 4. D.
Варианты ответов: 1. А. 2. В. 3. С. 4. D.
5. Выберите верную эпюру распределения нормальных напряжений при изгибе (рис. 33.9). Напишите формулу для расчета нормальных напряжений при изгибе. Изгибающий момент действует в вертикальной плоскости.
6. Как изменится максимальное нормальное напряжение в сечении (рис. 33.10а), если балку прямоугольного сечения положить плашмя (рис. 33.10б)? b = 20 мм; h = 100 мм.
7. Во сколько раз увеличится прогиб балки, если распределенную по всей длине нагрузку заменить сосредоточенной, приложенной в середине пролета? Использовать формулы для определения прогибов, приведенные в таблице 33.1.
|
из
5.00
|
Обсуждение в статье: Расчёты на жесткость при изгибе |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

