Применение интерференции в технике

Явление интерференции света находит широкое применение в современной технике. Одним из таких применений является создание "просветленной" оптики. Отполированная поверхность стекла отражает примерно 4% падающего на нее света. Современные оптические приборы состоят из большого числа деталей, изготовленных из стекла. Проходя через каждую из этих деталей, свет ослабляется на 4%. Общие потери света в объективе фотоаппарата составляют примерно 25%, в призменном бинокле и микроскопе - 50% и т. д.
Для уменьшения световых потерь в оптических приборах все стеклянные детали , через которые проходит свет, покрывают пленкой, показатель преломления которой меньше показателя преломления стекла. Толщина пленки равна четверти длины волны.
Другим применением явления интерференции является получение хорошо отражающих покрытий, необходимых во многих отраслях оптики. В этом случае используют тонкую пленку толщиной l /4 из материала, коэффициент преломления которого n 2 больше коэффициента преломления n 3 . В этом случае отражение от передней границы происходит с потерей полволны, так как n 1 < n 2 , а отражение от задней границы происходит без потери полволны (n 2 >n 3 ). В результате разность хода d = l /4+ l /4+ l /2= l и отраженные волны усиливают друг друга.
Интерференции света широко используется при спектральном анализе для точного измерения расстояний и углов, в рефрактометрии, в задачах контроля кач-ва поверхностей, для создания светофильтров, зеркал, просветляющих покрытий и др.; на явлениях интерференции света. основана голография.
Важный случай интерференции света- интерференция поляризованных лучей.

19.Дифракция света. Принцип Гюйгенса-Френеля. Дифракция Френеля и дифракция Фраунгофера.

Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий. Как показывает опыт, свет при определенных условиях может заходить в область геометрической тени. Если на пути параллельного светового пучка расположено круглое препятствие (круглый диск, шарик или круглое отверстие в непрозрачном экране), то на экране, расположенном на достаточно большом расстоянии от препятствия, появляется дифракционная картина – система чередующихся светлых и темных колец. Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос.

Дифракционные явления были хорошо известны еще во времена Ньютона, но объяснить их на основе корпускулярной теории света оказалось невозможным. Первое качественное объяснение явления дифракции на основе волновых представлений было дано английским ученым Т. Юнгом. Независимо от него в 1818 г. французский ученый О. Френель развил количественную теорию дифракционных явлений. В основу теории Френель положил принцип Гюйгенса, дополнив его идеей об интерференции вторичных волн. Принцип Гюйгенса в его первоначальном виде позволял находить только положения волновых фронтов в последующие моменты времени, т. е. определять направление распространения волны. По существу, это был принцип геометрической оптики. Гипотезу Гюйгенса об огибающей вторичных волн Френель заменил физически ясным положением, согласно которому вторичные волны, приходя в точку наблюдения, интерферируют друг с другом. Принцип Гюйгенса–Френеля также представлял собой определенную гипотезу, но последующий опыт подтвердил ее справедливость. В ряде практически важных случаев решение дифракционных задач на основе этого принципа дает достаточно хороший результат. Рис. 1 иллюстрирует принцип Гюйгенса–Френеля.

Рисунок 1. Принцип Гюйгенса–Френеля. ΔS1 и ΔS2 – элементы волнового фронта, и – нормали

1. Дифракция Френеля. Размер препятствия порядка размера зоны Френеля. Их отношение оказывается порядка единицы:

(2.10)

Безразмерный параметр p называют волновым параметром. В этом случае справедливо френелевское приближение - в фазовом множителе расстояние r заменяют приближенным выражением

(2.11)

Амплитудный множитель 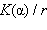заменяют приближенным выражением , не зависящим от переменных интегрирования (при условии, что размер препятствия мал по сравнению с расстоянием до плоскости наблюдения). Указанные выше приближения используются при рассмотрении дифракции на экранах с осевой симметрией и на одномерных препятствиях.

Таким образом, в области френелевской дифракции (так называемая ближняя волновая зона) выражение (2.9) записывается в виде

(2.12)

2. Дифракция Фраунгофера. Размер препятствия много меньше размера зоны Френеля и, следовательно,

(2.13)

Неравенство (2.13) означает, что дифракционная картина наблюдается на достаточно удаленном экране (в пределе – на бесконечности). В этом случае радиусы-векторы , проведенные от различных точек экрана к точке наблюдения практически параллельны друг другу. Это обстоятельство резко упрощает фазовые соотношения. В области дифракции Фраунгофера в фазовом множителе можно приближенно положить

(2.14)

где – расстояние от центра экрана до точки наблюдения Р. В амплитудном множителе, как и в случае френелевской дифракции, выражение 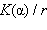заменяют на . В области дифракции Фраунгофера

(2.15)

Следует подчеркнуть, что выражение (2.15) имеет вид двумерного преобразования Фурье функции (см. главу 1.2.3) - граничного возмущения в плоскости z = 0. Область дифракции Фраунгофера принято называть дальней волновой зоной.

Таким образом, критерием наблюдения дифракционных картин различного вида может служить значение волнового параметра . При наблюдается френелевская дифракция. Характерная качественная особенность френелевских дифракционных картин состоит в том , что область наблюдения дифракции приблизительно совпадает с границами геометрической тени. Например, при освещении плоской волной отверстия диаметра D в непрозрачном экране, размер дифракционной картины в плоскости z = b окажется порядка D. При 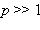наблюдается дифракция Фраунгофера. В этом случае дифракционная картина значительно шире размеров геометрической тени. Второй важной особенностью фраунгоферовских дифракционных картин, в отличие от френелевской дифракции, является то, что при разных положениях плоскости наблюдения дифракционные картины подобны друг другу; при переходе к другой плоскости наблюдения изменяется только масштаб картины. По этому признаку наблюдаемые на экране дисплея дифракционные картины легко можно отнести к френелевской или фраунгоферовой дифракции.

Отметим здесь, что фраунгоферова дифракция может наблюдаться в фокальной плоскости линзы (см. главу 8). Параллельный пучок лучей, распространяющийся под углом к оси (рис. 2.11), сводится линзой в некоторой точке фокальной плоскости без нарушения фазовых соотношений (таутохронизм). Поэтому распределение поля в фокальной плоскости в некотором масштабе воспроизводит дифракционную картину, которую можно наблюдать в отсутствие линзы на достаточно удаленной плоскости наблюдения. В оптических инструментах, как правило, наблюдается дифракция Фраунгофера.

Рисунок 2.11. Наблюдение дифракции Фраунгофера в фокальной плоскости линзы.