 |
Главная |
Дифракция Фраунгофера на щели. Дифракционная расходимость светового пучка
|
из
5.00
|
Наибольший практический интерес представляют дифракционные явления, наблюдаемые при падении на экран или отверстие в экране параллельного пучка света. В результате дифракции пучок утрачивает параллельность, то есть появляется свет, распространяющийся в направлениях, отличных от первоначального. Распределение его интенсивности на очень большом расстоянии от экрана соответствует дифракции Фраунгофера. Волны, возникающие в результате ограничения падающей плоской волны при прохождении сквозь отверстие на экране, называются дифрагировавшими, а нормали к их волновым поверхностям – дифрагировавшими лучами.
Дифрагировавшие лучи не существуют в рамках геометрической оптики. Возникновение дифрагировавших волн при прохождении через отверстие означает, что волна с ограниченной площадью поперечного сечения не может быть строго плоской.
 Рис. 3.17
Рис. 3.17
|
Рассмотрим дифракцию Фраунгофера на одной щели. Пусть на бесконечно длинную щель падает плоская световая волна (рис. 3.17). Поместим за щелью собирающую линзу, а в фокальной плоскости линзы – экран. Фронт падающей волны, плоскость щели и экран параллельны друг другу.
Распределение интенсивности света при дифракции Фраунгофера можно найти с помощью принципа Гюйгенса–Френеля. Интенсивность в точке экрана Р обусловлена интерференцией вторичных волн, исходящих от всех элементарных участков щели. Причем эти волны распространяются в одном и том же направлении, характеризуемом углом j. Заметную интенсивность имеют при этом лишь волны, дифрагировавшие на малые углы.
Когда размеры отверстия велики по сравнению с длиной волны, напряженность поля на поверхности, совпадающей с плоскостью щели, можно считать такой же, какой она была в отсутствии экрана.
Разобьем открытую часть волновой поверхности на параллельные краям щели элементарные зоны шириной 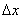 . Каждая такая зона становится источником вторичных волн. Вторичные волны, посылаемые этими зонами в направлении, определяемом углом j, соберутся в точке экрана Р. Каждая волна, испущенная элементарной зоной, создаст в точке Р колебание
. Каждая такая зона становится источником вторичных волн. Вторичные волны, посылаемые этими зонами в направлении, определяемом углом j, соберутся в точке экрана Р. Каждая волна, испущенная элементарной зоной, создаст в точке Р колебание  . Линза собирает в фокальной плоскости плоские волны. Поэтому амплитуда волны
. Линза собирает в фокальной плоскости плоские волны. Поэтому амплитуда волны  не зависит от расстояния до точки наблюдения. Ограничившись рассмотрением малых углов j, можно считать, что коэффициент
не зависит от расстояния до точки наблюдения. Ограничившись рассмотрением малых углов j, можно считать, что коэффициент  . Тогда амплитуда колебания, возбуждаемого зоной в любой точке экрана, будет зависеть только от площади зоны. Площадь зоны пропорциональна ее ширине
. Тогда амплитуда колебания, возбуждаемого зоной в любой точке экрана, будет зависеть только от площади зоны. Площадь зоны пропорциональна ее ширине 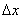 . Следовательно, колебания
. Следовательно, колебания  от каждой полоски имеют одинаковую амплитуду и отстают по фазе от колебания, создаваемого соседней полоской на одну и ту же величину
от каждой полоски имеют одинаковую амплитуду и отстают по фазе от колебания, создаваемого соседней полоской на одну и ту же величину  , зависящую от угла дифракции
, зависящую от угла дифракции  .
.
 Чтобы найти значение
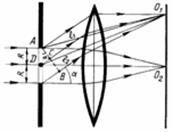
Чтобы найти значение  , проведем плоскость АВ, перпендикулярную к направлению дифрагировавших лучей (рис. 3.18). Собирающая линза обладает свойством, называемым таутохронностью: если свет по двум разным путям распространяется за одно и то же время, то пути называются таутохронными, то есть оптические длины этих путей равны между собой. Условию таутохронизма удовлетворяют все пути лучей, проходящих через линзу. Следовательно, линза не вносит дополнительной разности хода для дифрагировавших волн. Таким образом, достаточно определить разность хода
, проведем плоскость АВ, перпендикулярную к направлению дифрагировавших лучей (рис. 3.18). Собирающая линза обладает свойством, называемым таутохронностью: если свет по двум разным путям распространяется за одно и то же время, то пути называются таутохронными, то есть оптические длины этих путей равны между собой. Условию таутохронизма удовлетворяют все пути лучей, проходящих через линзу. Следовательно, линза не вносит дополнительной разности хода для дифрагировавших волн. Таким образом, достаточно определить разность хода  , возникающую на пути от плоскости щели до плоскости АВ. Величина
, возникающую на пути от плоскости щели до плоскости АВ. Величина  связана с разностью хода соотношением
связана с разностью хода соотношением  . Тогда, как видно из рис. 3.18,
. Тогда, как видно из рис. 3.18,  .
.
Дифракционная расходимость светового пучка - увеличение размеров поперечно-ограниченного светового пучка при его распространении сквозь окружающую среду, которая выражается через уравнения Максвелла и преобразования Фурье.
Любые пучки света, пространственно ограниченные по поперечным координатам, подвержены “поперечному расплыванию” по мере распространения. Это свойство электромагнитного излучения называется дифракцией света.
дифракционная расходимость поперечно-ограниченного пучка:

Дифракционная решетка - система препятствий (параллельных штрихов), сравнимых по размерам с длиной волны.
Величина d = a + b называется постоянной (периодом) дифракционной решетки, где а — ширина щели; b — ширина непрозрачной части. Уголj - угол отклонения световых волн вследствие дифракции. Наша задача - определить, что будет наблюдаться в произвольном направлении j - максимум или минимум. Оптическая разность хода  Из условия максимума интерференции получим: Из условия максимума интерференции получим: 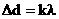 . Следовательно: . Следовательно:  - формула дифракционной решетки. Величина k — порядок дифракционного максимума
( равен 0, ± 1, ± 2 и т.д.). - формула дифракционной решетки. Величина k — порядок дифракционного максимума
( равен 0, ± 1, ± 2 и т.д.).
| 

|
Определениеlс помощью дифракционной решетки
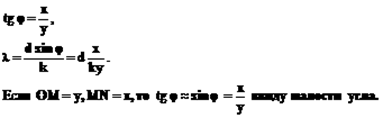
| 
|
|
из
5.00
|
Обсуждение в статье: Дифракция Фраунгофера на щели. Дифракционная расходимость светового пучка |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

