 |
Главная |
ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
|
из
5.00
|
ПЕРВИЧНАЯ ОБРАБОТКА
Методические указания по контрольной работе № 6
для студентов заочного факультета всех специальностей и варианты заданий
Магнитогорск
2014 г.
ВВЕДЕНИЕ
Основной задачей современной математической статистики, методы которой опираются на теорию вероятностей, является научная оценка результатов измерений. В таких задачах, как контроль качества продукции, подвергнуть контролю всю продукцию практически невозможно и особенно в тех случаях, где контроль связан с разрушением пробы или изделия, например, при испытании ламп и электронных трубок на долговечность и т.п.
Именно здесь и приходят на помощь методы математической статистики, посредством которых можно по известным свойствам некоторого подмножества объектов, взятого из совокупности, судить о неизвестных свойствах всех объектов, принадлежащих данной совокупности.
Задачи математической статистики состоят:
1) в указании способа группировки статистических данных,
2) в разработке методов анализа статистических данных:
а) оценки неизвестных функций распределения, плотности распределения вероятностей, оценки зависимости между случайными величинами,
б) проверки статистических гипотез о виде неизвестных распределений и т.д.
В данной разработке содержатся методические рекомендации для студентов заочного отделения при подготовке и выполнении контрольной работы № 6, вопросы для подготовки и сдачи теоретической части и подробные указания по выполнению практической, снабженные соответствующими примерами всех расчетов.
Для изучения теории и выполнения работы рекомендуется следующая литература:
- Краснов М.Л., Киселев А.И. и др. Вся высшая математика: Учебник. Т. 5.- М.: Эдиториал УРСС, 2001.- 296 с.
- Гмурман В.Е. Теория вероятностей и математическая статистика.- Учебн. пособие для вузов. - М.: Высш. шк.,2003.-479 с.
- Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике.- Учебн. пособие для вузов. - М.: Высш. шк.,2002.-405 с.
- Горелова Г.В., Кацко И.А. Теория вероятностей и математическая статистика в примерах и задачах с применением EXCEL. Ростов-на-Дону: Феникс,2002. 348 с.
- Кимайкина Н.И. и др. Теория вероятностей и математическая статистика. Учебные карты. Магнитогорск, МГМИ, 1991. 20 с.
- Кимайкина Н.И., Кукушкина О.А. Элементы математической статистики. Методические указания к лабораторному практикуму. Магнитогорск: МГТУ, 2001. 30 с.
Теоретические вопросы
[Краснов и др. гл. XLIV, стр. 199 и далее,
Гмурман, гл. 16, §1-18, гл. 19, §1-6, 22, 23]
(какие понятия нужно знать, чтобы приступить к выполнению работы)
1. Генеральная и выборочная совокупности, способы организации выборки, объем совокупности, варианта, частота варианты, относительная частота варианты;
2. Статистический ряд, вариационный ряд, интервальный вариационный ряд, методика его получения группированием данных;
3. Эмпирическая функция распределения, способы её задания, полигон частот, гистограмма, выборочная оценка плотности вероятности.
4. Генеральные параметры (числовые характеристики) распределения - характеристики положения и рассеяния: математическое ожидание, дисперсия, среднее квадратичное отклонение.
5. Точечные и интервальные оценки параметров распределения.
6. Требования, предъявляемые к оценкам генеральных параметров (несмещенность, состоятельность, эффективность).
7. Статистическая проверка гипотез. Нулевая и конкурирующая, простая и сложная гипотезы.
8. Ошибки первого и второго рода.
9. Критерии значимости, критерии согласия.
10. Основные методы проверки нормальности распределения.
ХОД РАБОТЫ
1. Перед вами (в вашем варианте) сто пар чисел (Х) – статистический ряд объёма n =100. Запишите минимальное и максимальное значения совокупности Х (статистического ряда):  . Для этого можно воспользоваться, например, Microsoft Excel.
. Для этого можно воспользоваться, например, Microsoft Excel.
2. Найдите размах варьирования измеримого признака:
 .
.
3. Выберите число интервалов равным .
Замечание: Выбор r зависит от объёма n, размаха R и от цели статистического исследования. Принято, чтобы получилось не менее 6 и не более 20 интервалов. Одна из формул r=[1+3,2 lg n],т.е. r целая часть числа 1+3,2 lg n.
4. Определите, чему равен шаг варьирования признака (длина интервала будущего вариационного ряда Х).
 .
.
5. Теперь найдем границы интервалов каждого признака таким образом, чтобы минимальное значение стало серединой первого интервала, а максимальное – серединой последнего. Для этого отступим от  и
и  на полшага, а к правому концу каждого интервала будем прибавлять длину шага:
на полшага, а к правому концу каждого интервала будем прибавлять длину шага:
 ,
,  ,
,  ,
,
 ,
,  ;
;  ;
;
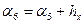 ;
;  ;
;  .
.
Таким образом, фактическое число интервалов совокупности равно 8.
(Убедитесь в правильности своих подсчетов: значение  должно быть больше максимального значения
должно быть больше максимального значения  на полшага.)
на полшага.)
6. Найдем середины получившихся интервалов:
 ,
,  ,
,  ,
, 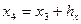 ,
,
 ,
,  ,
, 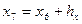 ,
,  . Проверка:
. Проверка:  .
.
7. Составьте вариационный ряд измеримого признака Х .
Таблица 1
| х | 
| 
| 
| 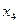
| 
| 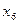
| 
| 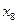
|
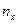
| 
| 
| 
| 
| 
| 
| 
| 
|
Здесь  - число значений
- число значений  , попавших в соответствующий интервал
, попавших в соответствующий интервал  .
.
Интер-валы

|
Середины интерв.
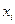
| Частоты |
Плотность относительн. частот

| |||
Абсолютн.

|
Относительн.

|
Накоплен. абсолютн.

|
Накопленная относительн.

| |||

| 
| 
|  / 100 / 100
|  =0 =0
|  =0 =0
| 
|

| 
| 
|  / 100 / 100
|  = = 
|  = = 
| 
|
| … | … | … | … | … | … | … |
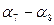
| 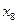
| 
|  / 100 / 100
|  =100- =100- 
|  =1- =1- 
| 
|

|
(Проверьте: сумма абсолютных частот  , где n – объём выборки.)
, где n – объём выборки.)
8. Заполните таблицу «Статистическая совокупность» :
Таблица 2
Статистическая совокупность измеримого признака Х
9. По данным таблицы 2, постройте (см. пример):
а) полигон и гистограмму распределения – графические оценки плотности распределения вероятностей генеральной совокупности;
б) полигон накопленных относительных частот– график эмпирической функции распределения:
 .
.
10. Заполните расчетную таблицу, взяв данные для первых трех столбцов в таблице 2:
Таблица 3
Расчет выборочных оценок признака Х
Серед
Инт.
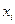
|
Частота

| Относит. частота

|
 
|

|

|

|

|
| … | … | … | … | … | … | … | … |

| n | 
| 
| 
| 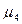
|
11. Запишите расчетные формулы для сгруппированных в r интервалов данных:
выборочного среднего  ;
;
выборочной дисперсии  ;
;
выборочного среднеквадратичного отклонения  ;
;
выборочной асимметрии  ;
;
выборочного эксцесса  .
.
12. Найдите исправленные оценки (статистики) генеральных параметров:
- выборочное среднее  =
=  ;
;
- исправленная дисперсия  ;
;
- исправленное среднеквадратичное отклонение  ;
;
-исправленная асимметрия  ;
;
- исправленный эксцесс  .
.
13. Найти моду и медиану по сгруппированным данным:
 , где
, где
 - середина интервала (модального) с наибольшей частотой
- середина интервала (модального) с наибольшей частотой  ;
;
 - нижняя граница модального интервала (левый конец отрезка, на котором самое большое значение частоты
- нижняя граница модального интервала (левый конец отрезка, на котором самое большое значение частоты  );
);
h – длина интервала (смотри лаб. раб. № 1);
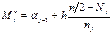 , где
, где
 - середина интервала (медианного), содержащего накопленную частоту
- середина интервала (медианного), содержащего накопленную частоту 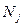 , не превосходящую половины выборки
, не превосходящую половины выборки  (
( 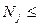
 );
);
 - нижняя граница медианного интервала;
- нижняя граница медианного интервала;
 и
и 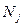 - частота и накопленная частота соответственно этого интервала.
- частота и накопленная частота соответственно этого интервала.
14. Для проверки гипотезы Но: генеральная совокупность измеримого признака, из которой извлечена выборка, распределена при данном уровне значимости  =0,05 по нормальному закону с плотностью
=0,05 по нормальному закону с плотностью
 , где
, где
а и  - параметры нормального распределения, необходимо:
- параметры нормального распределения, необходимо:
- объединить интервалы (смотри пример) с абсолютными частотами  , меньшими 5 , суммируя частоты;
, меньшими 5 , суммируя частоты;
- отметить, чему равно теперь r – число интервалов;
- записать число к - степеней свободы и по таблицам найти  ,k=r-s-1, r-число интервалов,s-число параметров распределения (s=2);
,k=r-s-1, r-число интервалов,s-число параметров распределения (s=2);
- заполнить расчетную таблицу для вычисления 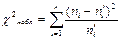 :
:
Таблица 4
Проверка гипотезыНо по критерию Пирсона
Левая граница
интерв.

| Правая гран.
нтер.

|
Абс.
Частота

| Zi=
= 
| Ф(zi) |

|
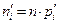
|

|
| … | … | … | … | … | … | … | … |

|  1 1
| 
|
где Ф(zi) – значение функции Лапласа для значений zi, записанных в предыдущем столбце,
 =
=  Ф - теоретическая вероятность попадания случайной величины Х, распределенной нормально, в интервал
Ф - теоретическая вероятность попадания случайной величины Х, распределенной нормально, в интервал  -
-  (значение функции Лапласа можно найти по таблице приложения 2
(значение функции Лапласа можно найти по таблице приложения 2
(см. [3] или [5])).
ПРИМЕР. На заводе железобетонных изделий N для создания марки бетона высокого качества проводилось исследование 100 различных пробных сортов бетона, для которых подсчитывался процент прочности на сжатие (случайная величина Х) и процент сопротивления того же сорта бетона на разрыв (случайная величина У). Получен следующий результат
Статистический ряд. Исходные значения величин
| Х, тыс.км. | У, % | Х, тыс.км. | У, % | Х, тыс.км. | У, % | Х, тыс.км. | У, % | Х, тыс.км. | У, % |
| 38,4 | 18,7 | 40,7 | 30,3 | 27,3 | 25,1 | ||||
| 40,2 | 11,7 | 50,8 | 28,4 | 15,7 | 20,6 | 28,6 | |||
| 24,1 | 20,9 | 38,2 | 22,8 | 47,6 | 11,3 | 52,8 | 15,2 | 19,5 | 19,7 |
| 32,5 | 22,4 | 19,8 | 30,3 | 21,3 | 24,5 | 20,3 | |||
| 29,5 | 35,7 | 15,3 | 30,5 | 27,8 | 28,7 | 27,8 | 15,5 | ||
| 38,1 | 19,6 | 34,3 | 20,7 | 48,7 | 11,5 | 32,5 | 35,2 | 30,7 | |
| 16,8 | 32,2 | 43,8 | 16,8 | 18,3 | 57,1 | 2,9 | 41,6 | 18,2 | |
| 28,8 | 29,7 | 35,5 | 23,9 | 20,2 | 23,8 | 42,5 | 15,3 | ||
| 47,1 | 14,7 | 45,9 | 54,3 | 14,2 | 50,7 | 15,9 | 32,9 | 22,5 | |
| 50,1 | 15,9 | 29,3 | 21,9 | 60,8 | 27,2 | 58,6 | 9,3 | 35,6 | 22,7 |
| 30,2 | 54,2 | 14,2 | 21,4 | 19,8 | 40,1 | 17,4 | 17,3 | ||
| 36,9 | 23,2 | 59,8 | 6,1 | 38,4 | 34,4 | 23,4 | 31,4 | 30,2 | |
| 36,6 | 7,9 | 32,2 | 22,3 | 46,8 | 20,5 | 53,7 | 12,4 | 28,2 | |
| 15,4 | 6,1 | 23,8 | 18,3 | 42,1 | 28,5 | 33,7 | 19,8 | ||
| 31,2 | 24,2 | 37,9 | 32,6 | 20,2 | 27,6 | 18,5 | |||
| 16,2 | 25,2 | 51,2 | 14,2 | 30,6 | 21,5 | 23,5 | 14,6 | 36,8 | 10,7 |
| 49,7 | 15,9 | 32,2 | 20,4 | 24,5 | 32,9 | 25,8 | 45,5 | 14,8 | |
| 49,7 | 19,5 | 30,9 | 20,7 | 57,6 | 20,3 | 14,4 | 18,6 | 15,3 | |
| 42,3 | 19,7 | 41,5 | 10,8 | 41,9 | 14,6 | 42,3 | 23,5 | 25,8 | 27,4 |
| 35,7 | 11,9 | 41,2 | 9,8 | 34,1 | 26,3 | 58,8 | 9,2 | 39,2 | 17,5 |
Найти эмпирическое распределение признака Х, построить графическое отображение распределения.
|
из
5.00
|
Обсуждение в статье: ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

