 |
Главная |
Пример оформления работы
|
из
5.00
|
Ход работы:
1. 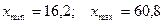 .
.
2. Размах варьирования: 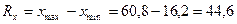 .
.
3. r=[1+3,2 lg n]= [1+3,2 lg 100=[7.4]=7;
4. Длина интервалов: 
5.Теперь найдем границы интервалов каждого признака таким образом, чтобы минимальное значение стало серединой первого интервала, а максимальное – серединой последнего. Для этого отступим от  и
и  на полшага, а к правому концу каждого интервала будем прибавлять длину шага:
на полшага, а к правому концу каждого интервала будем прибавлять длину шага:
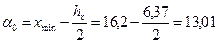 ;
; 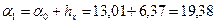 ;
;
 ;
; 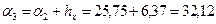 ;
;
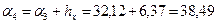 ;
; 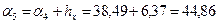 ;
;
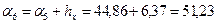 ;
; 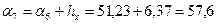 ;
;
 .
.
Таким образом, фактическое число интервалов совокупности равно 8.
Убедимся в правильности своих подсчетов: действительно, значения  =63,97 больше максимального значения
=63,97 больше максимального значения  =60,8 .
=60,8 .
6.Найдем серединыполучившихся интервалов: 
 ;
; 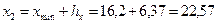 ;
;
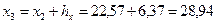 ;
; 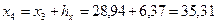 ;
; 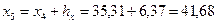 ;
; 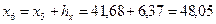 ;
;
 ;
;  .
.
О верности подсчетов свидетельствует равенство (возможно приближенное) последних, восьмых, значений соответственно  .
.
7. Запишем вариационный ряд признака Х.
Таблица 2
| х | 
| 
| 
| 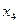
| 
| 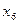
| 
| 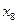
|
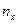
|
8.Заполним таблицу «Статистическая совокупность» для признака Х:
Таблица 3
Статистическая совокупность измеримого признака Х
| Интервалы α i-1 – α i |
Середины интерв.
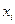
| Частоты |
Плотность относительн. частот

| |||
Абсолютн.

|
Относительн.

|
Накоплен. абсолютн.

|
Накопленная относительн.

| |||
| 13.01-19.38 | 16.2 | 0.04 | 0.0063 | |||
| 19.38-25.75 | 22.57 | 0.08 | 0.04 | 0.0126 | ||
| 25.75-32.12 | 28.94 | 0.2 | 0.12 | 0.0314 | ||
| 32.12-38.49 | 35.31 | 0.26 | 0.32 | 0.0408 | ||
| 38.49-44.86 | 41.68 | 0.15 | 0.58 | 0.0235 | ||
| 44.86-51.23 | 48.05 | 0.15 | 0.73 | 0.0235 | ||
| 51.23-57.6 | 54.42 | 0.08 | 0.88 | 0.0126 | ||
| 57.6-63.97 | 60.8 | 0.04 | 0.96 | 0.0063 | ||

|
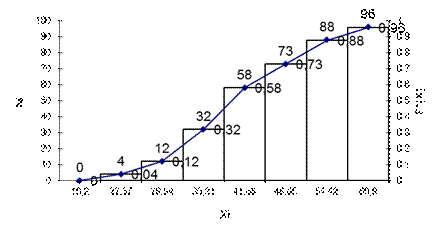
9. Построим полигон (ломаная линия) и гистограмму («столбики») распределения, затем – полигон накопленных частостей (рис. 1 и 2)
Рисунок 1Полигон и гистограмма распределения признака 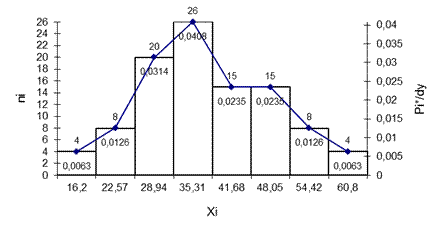
Рисунок 2
Эмпирическая функция распределения F*(X)
10.Начинаем заполнение расчетной таблицы для нахождения выборочных оценок:
Таблица 3
Расчет выборочных оценок признака Х
Серед
Инт.
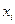
| Частота

| Относит частота

|
 
|

|

|

|

|
| 16,2 | 0.04 | 0,648 | -21,467 | 18,434 | -395,724 | 8495,123 | |
| 22,57 | 0.08 | 1,8056 | -15,097 | 18,234 | -275,288 | 4156,111 | |
| 28,94 | 0.2 | 5,788 | -8,7273 | 15,233 | -132,944 | 1160,245 | |
| 35,31 | 0.26 | 9,1806 | -2,3573 | 1,4448 | -3,40579 | 8,02847 | |
| 41,68 | 0.15 | 6,252 | 4,0127 | 2,4153 | 9,691731 | 38,89001 | |
| 48,05 | 0.15 | 7,2075 | 10,383 | 16,170 | 167,889 | 1743,141 | |
| 54,42 | 0.08 | 4,3536 | 16,753 | 22,452 | 376,1356 | 6301,287 | |
| 60,8 | 0.04 | 2,432 | 23,133 | 21,405 | 495,1525 | 11454,21 | |

|  =
37,667 =
37,667
|  115,7885
115,7885
|  =
241,5064 =
241,5064
| 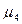 =
33357,04 =
33357,04
|
11. Выборочные оценки для признака Х находим по данным таблицы 5 и формулам для сгруппированных данных:
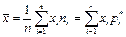 = 37,667;
= 37,667;
 = 115,7885;
= 115,7885;
 = 10,76;
= 10,76;
 = 0,19;
= 0,19; 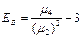 = -0,51.
= -0,51.
12. Исправленные оценки признака Х:
- выборочное среднее  =
=  = 37,67;
= 37,67;
- исправленная дисперсия  = 116,958;
= 116,958;
- исправленное среднеквадратичное отклонение 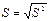 = 10,81;
= 10,81;
-исправленная асимметрия 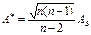 = 1,015*0,19=0,193;
= 1,015*0,19=0,193;
- исправленный эксцесс 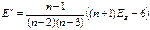 = -0,47.
= -0,47.
13.Найдем моду и медиану по сгруппированным данным признака Х:
 =26 – наибольшая частота, (32.12-38.49) – модальный интервал,
=26 – наибольшая частота, (32.12-38.49) – модальный интервал, 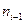 =20;
=20; 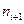 =15;
=15;  тогда мода
тогда мода
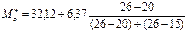 =34,37.
=34,37.
Накопленная частота 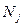 =32, не превосходящая половины выборки
=32, не превосходящая половины выборки  =100/2=50 (
=100/2=50 ( 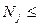
 ); (32.12-38.49) – медианный интервал; тогда медиана
); (32.12-38.49) – медианный интервал; тогда медиана
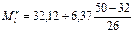 =36,53.
=36,53.
Выводы: а) 

 ,
,
б) А* = 0,193 – больше нуля, значит полигон распределения скошен, правая ветвь длиннее левой, начиная от вершины: левосторонняя асимметрия. А* близко к нулю.
Е* = -0,47 – меньше нуля, гистограмма – плосковершинная (по сравнению с нормальным распределением).
г) Можно предположить, что выборка произведена из генеральной совокупности, имеющей нормальное распределение.
14. Проверим, взята ли данная выборка (для измеримого признака Х) из нормально распределенной генеральной совокупности.
( помним, что  =37,67 и
=37,67 и 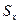 =10,81.)
=10,81.)
Формулируем статистическую гипотезу Но: генеральная совокупность измеримого признака Х, из которой извлечена выборка, распределена по нормальному закону при данном уровне значимости  =0,05, с плотностью
=0,05, с плотностью
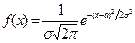 , где
, где
а и  - параметры нормального распределения.
- параметры нормального распределения.
а) Выпишем границы интервалов и абсолютные частоты в них
| Интервалы α i-1 – α i |
Середины интерв.
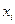
|
Абсолютн. частота

|
| 13.01-19.38 | 16.2 | |
| 19.38-25.75 | 22.57 | |
| 25.75-32.12 | 28.94 | |
| 32.12-38.49 | 35.31 | |
| 38.49-44.86 | 41.68 | |
| 44.86-51.23 | 48.05 | |
| 51.23-57.6 | 54.42 | |
| 57.6-63.97 | 60.8 |
Видим, что в первом и последнем интервалах абсолютная частота меньше пяти. Объединяем первые два и последние два интервала, число интервалов r равно теперь 6, значит число степеней свободы к = r – 3 = 3 и  =
= 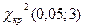 =7,8.
=7,8.
б) Заполняем расчетную таблицу:
Таблица 4
Проверка гипотезыНо по критерию Пирсона
Левая граница
интерв.

| Правая гран.
нтерв.

|
Абс.
Частот

| Zi=

| Ф(zi) |

|
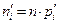
|

|
| 13,01 | 25,75 | -2,28 | -0,4887 | 0,1244 | 0,01 | ||
| 25,75 | 32,12 | -1,10 | -0,3643 | 0,1693 | 0,56 | ||
| 32,12 | 38,49 | -0,51 | -0,1950 | 0,2269 | 0,48 | ||
| 38,49 | 44,86 | -0,08 | 0,0319 | 0,2167 | 2,05 | ||
| 44,86 | 51,23 | 0,67 | 0,2486 | 0,1458 | 0,01 | ||
| 51,23 | 63,97 | 1,25 | 0,3944 | 0,1029 | 0,28 | ||

| 2,80 | 0,4973 |  1 1
|  =3,4 =3,4
|
Получили, что  =3,4 – меньше, чем
=3,4 – меньше, чем  =7,8, значит гипотеза нормальности распределения принимается.
=7,8, значит гипотеза нормальности распределения принимается.
в) Запишем формулу плотности теоретического распределения f(x): принимаем а =37,67,  =10,81. Итак, теоретическая функция распределения измеримого признака Х
=10,81. Итак, теоретическая функция распределения измеримого признака Х
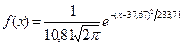 .
.
210100 преп. Вахрушева И.А.
|
из
5.00
|
Обсуждение в статье: Пример оформления работы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

