Равномерное распределение

с.в. ξ принимает значении 1,…,N с вероятностями 1/N.

Нормальное распределение:

 

где Φ(u) − интеграл Лапласа, для которого есть таблицы

M=a

D= σ²

Пуассоновское распределение:

С.в ξ имеет Пуассоновское распределение с параметром λ>0, если:

где к = 0,1,…

Экспоненциальное распре-деление:

, x>=0

, x>=0

 

 

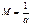
Рассмотрим с.в. , по теореме она имеет распредел . - плотность этого распредел-я.

Пусть задан уровень доверия р, найдем 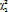и , такие, что:

Метод моментов:

Пусть Q – некоторый числовой пар-р случайной величины , x₁…x_n – случайная выборка.

Составляем к – уравнений приравнивая теоретическую функцию момента к-го порядка и его найденное на основании выборки значение.

Решая данную сист находим необходимые параметры.

Метод максим правдоподоб:

Оцениваемы параметры д принимать такие значения, чтобы вероятность получить такую выборку была максимальна.

Пусть с.в. η - дискретна

Вариационный ряд – y₁…y_k

Вероятности получения таких y_k – p₁(Q)…p_k(Q)

Представим выборку в виде вариационного ряда частот:

y₁…y_k

n₁…n_k

Вероятность получить такой ряд: P(x₁…x_k, Q) =

Ищем максимум L, тем самым находим Q

Пусть с.в. - непрерывна

- вероятность получить конкретное значение.

Отойдем от х влево в право на , тогда

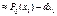, где - плотность

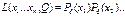
- не зависит от Q, значит эту часть можно исключить из формулы.

Тогда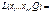

Ищем максимум L, тем самым находим Q

49 Линейная регрессия (постановка зад и статистич оценки пар-ров регрессии)

Идея линейной регрессии заключается в предполож, что две с.в. находятся в линейной зависимости друг от друга . Таким образом, основной задачей линейной регрессии явл-ся нахождение коэффиц k и b.

Для их нахождения построим функцию , которая показывает меру отличия двух случайных величин. Искомыми коэф-фициентами будут считаться те, при кот данная функция достигнет минимума.

Для нахождения экстремума функции необходимо решить систему уравнений:

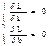
1.

=>

 

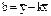
50 Слачайные процессы (Марковский и пуассоновский)

Случ проц – совокупность случ величин ξ= ξ(t), где t ∈θ (множ моментов времени)

Пусть t₀∈θ, тогда ξ(t), при t<t₀ будем назыв прошлым, ξ(t₀) настоящим, при ξ(t) при t>t₀ будущим.

Марковский проц - случ процесс, эволюция кот после любого заданного значения временного параметра t не зависит от эволюции, предшествовавшей t, при условии, что значение процесса в этот момент фиксировано.

Пусть t₁<…<t_k<t (1..k-1 прошл, k настоящ), x₁,…,x_k,x∈X соответст им значен случ проц, то p(ξ(t)=x| ξ(t₁)=x₁,…, ξ(t_k)=x_k)=p(ξ(t)=x| ξ(t_k)=x_k), то ξ(t) – марк сл проц.

Марковск сл проц называется цепью Маркова, если X∈{0}∪N.

Цепь Маркова ξ(t) наз-ся цепью с непр временем, если θ – интервал полож длины из R¹, а Х не более чем счетно. Цепь М наз-ся однородной, если вероятности перехода за 1 шаг не зависят от номера шага n для ∀ i,j∈X, где – вер пер.

51 Основные понятия теории массового обслуж (входящий поток, поток обслуж, дисциплины обслуж, классификация Кендела)

В ТМО рассматриваются системы (СМО), реализующ многократное выполнение однотипных задач. Например: очередь в кассу, телефонные сети и т.д. Всякая СМО предназначена для обслуживания некоторого потока заявок, идущих на вход. Обычно поток событий случаен. При поступлении на вход, заявки могут образовывать очередь. После обслуживания заявка выходит из СМО.

В качестве характеристик функционирования СМО выделяют:

1. Эффективность испо-льзования СМО

Абсолютная пропускная способность – среднее число обслуживаемых в единицу времени заявок

Относительная пропускная способность СМО – отношение среднего числа заявок, обслуженных в единицу времени, к среднему числу поступивших заявок

Средняя продолжительность занятости СМО

Коэффициент использования СМО – отношение времени, в течении которого СМО занята, к общему времени

2. Качество обслуживания заявок

*Среднее время ожидания заявки в очереди

*Среднее время пребывания заявки в СМО

*Вероятность отказа заявке в СМО без ожидания

 

52 Постановка задачи дискр анализа и линейный классификатор

Дискриминантный анализ - раздел вычислительной математики, представляющий основное средство решения задач Распознавания образов (принятие решений на основе статистики).

Задача обучения с учителем. Постановка задачи:

Пусть есть n признаков, каждый объект – точка в пространстве Rⁿ, X – множество объектов, Х =(х₁…х_n)

Пусть m классов k₁…k_m и x¹…x^p - обучающая после-довательность

x¹ …. x^p1 принадлежит k¹

x^p1+1 …. x^p2 принадлежит k²

…………………………..

x^Pm-1 …. x^Pm принадлежит k^m

Есть эл-т x. необх опр-ть к какому классу он принадлежит

 

 

 

2.

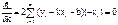
| делим на n

| подставляем

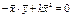
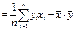
Ковариация:

Дисперсия:

Тогда:

, => ,

 

 

Если число сост конечно, то однор цепь Маркова называется конечной. Она задается матричей вероят-ности перехода за 1 шаг P. Матр вер-й перехода за n шагов P⁽ⁿ⁾=P*P*..*P.

Пуассоновский процесс

Это такой процесс, в котором время между событиями имеет экспоненциальное распределение.