Прямоугольная декартова система координат в пространстве

Упорядоченная система трёх взаимно перпендикулярных осей с общим началом отсчёта (началом координат) и общей единицей длины называется прямоугольной декартовой системой координат в пространстве.

В этой упорядоченной системе координатных осей 0xyz ось Ox называется осью абсцисс, ось 0y – осью ординат, и ось 0z – осью аппликат.

С произвольной точкой М пространства свяжем вектор

,

называемый радиус-вектором точки М и спроецируем его на каждую из координатных осей. Обозначим величины соответствующих проекций:

Числа x, y, z называются координатами точки М , соответственно абсциссой,ординатой и аппликатой, и записываются в виде упорядоченной точки чисел: M (x; y; z) (рис.6).

Вектор единичной длины, направление которого совпадает с направлением оси, называют единичным вектором(или ортом) оси. Обозначим через

Соответственно орты координатных осей Ox, Oy, Oz

Теорема. Всякий вектор может быть разложен по ортам координатных осей:

(2)

Равенство (2) называется разложением вектора по координатным осям. Коэффициентами этого разложения являются проекции вектора на координатные оси. Таким образом, коэффициентами разложения (2) вектора по координатным осям являются координаты вектора.

После выбора в пространстве определённой системы координат вектор и тройка его координат однозначно определяют друг друга, поэтому вектор может быть записан в форме

(3)

Представления вектора в виде (2) и (3) тождественны.

Условие коллинеарности векторов в координатах

Как мы уже отмечали, векторы называются коллинеарными, если они связаны отношением

.

Пусть даны векторы . Эти векторы коллинеарны, если координаты векторов связаны отношением

,

то есть, координаты векторов пропорциональны.

Пример 4. Даны векторы 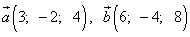. Коллинеарны ли эти векторы?

Решение. Выясним соотношение координат данных векторов:

.

Координаты векторов пропорциональны, следовательно, векторы коллинеарны, или, что то же самое, параллельны.

Длина вектора

Вследствие взаимной перпендикулярности координатных осей длина вектора

равна длине диагонали прямоугольного параллелепипеда, построенного на векторах

и выражается равенством

(4)

Вектор полностью определяется заданием двух точек (начала и конца), поэтому координаты вектора можно выразить через координаты этих точек.

Пусть в заданной системе координат начало вектора находится в точке

а конец – в точке

(рис.8).

Тогда

Из равенства

следует, что

Отсюда

или в координатной форме

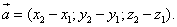(5)

Следовательно, координаты вектора равны разностям одноимённых координат конца и начала вектора. Формула (4) в этом случае примет вид

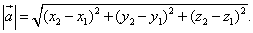(6)

Пример 5.Найти длину вектора x = (3; 0; 4).

Решение. Длина вектора равна

Пример 6.Даны точки:

Выяснить, равнобедренный ли треугольник, построенный на этих точках.

Решение. По формуле длины вектора (6) найдём длины сторон и установим, есть ли среди них две равные:

Две равные стороны нашлись, следовательно необходимость искать длину третьей стороны отпадает, а заданный треугольник является равнобедренным.

К началу страницы