 |
Главная |
Краткие теоретические сведения. Ламинарный и турбулентный режимы движения
|
из
5.00
|
Ламинарный и турбулентный режимы движения.
Опыты Рейнольдса.
Рассматривая жидкость как идеальную, мы пренебрегаем ее вязкостью. Это приводит к тому, что сопротивление тела, равномерно движущегося в неограниченном пространстве, оказывается равным нулю, а это противоречит данным опытов с реальными жидкостями. В реальных жидкостях со стороны слоя, движущегося медленно, действуют силы, замедляющие движение частиц слоя, движущегося с большей скоростью и, наоборот, частицы слоя с большей скоростью ускоряют более медленный слой. При малых скоростях движения жидкости один слой скользит по другому. Слой у стенки прилипает к ней. Силы вязкости пропорциональны изменению скорости потока в нормальном направлении к скорости. Наиболее сильно они будут сказываться там, где изменения скорости велики. Расположенная около поверхности тела (трубы, канала) область течения вязкой жидкости, в которой изменяется скорость, называется пограничным слоем.
Вне пограничного слоя влияние вязкости проявляется слабо и поведение вязкой жидкости близко к поведению идеальной. В вязкой жидкости складываются два движения: хаотичное движение молекул и направленное движение всего потока. С учетом этого можно уточнить понятие пограничного слоя. Пограничный слой представляет собой область течения вязкой жидкости, в которой силы трения и инерции имеют одинаковый порядок.
Многочисленными наблюдениями и опытами установлено, что существует два основных режима движения жидкостей: ламинарный и турбулентный.
При ламинарном режиме вся масса жидкости движется параллельными скользящими друг по другу несмешивающимися струйками или слоями.
При турбулентном режиме отдельные частицы жидкости движутся по произвольным сложным траекториям, струйки перемешиваются, и поток жидкости представляет собой беспорядочно движущуюся массу.
 Впервые предположение о существовании двух режимов движения жидкости высказал Д.И.Менделеев в 1880 г. Позднее оно было подтверждено опытным путем О.Рейнольдсом в 1883 г. Он пропускал воду через стеклянные трубки разного диаметра, регулируя скорость движения воды в них кранами 1 и 5 (рис.1). По тонкой трубке 3 с заостренным концом к входу
Впервые предположение о существовании двух режимов движения жидкости высказал Д.И.Менделеев в 1880 г. Позднее оно было подтверждено опытным путем О.Рейнольдсом в 1883 г. Он пропускал воду через стеклянные трубки разного диаметра, регулируя скорость движения воды в них кранами 1 и 5 (рис.1). По тонкой трубке 3 с заостренным концом к входу
Рис. 1. Экспериментальная установка О.Рейнольдса:
1, 5 — краны; 2 — сосуд с окрашенной жидкостью; 3 — трубка с заостренным концом;
4 — трубка; 6 — сосуд; 7 — сливная трубка
в стеклянную трубку 4 подводилась окрашенная жидкость из сосуда 2. Средняя скорость в трубке 4 площадью сечения ω определялась по объему воды W, поступившей в сосуд 5 за время t: v = W/(ωt).
Опыты, проводившиеся при постоянном напоре (для его поддержания была использована сливная трубка 7), показали, что при малых скоростях движения воды в трубке 4 краска движется в ней в виде тонкой струйки параллельно стенке, не перемешиваясь с водой. После достижения определенной для данных условий опыта средней скорости движение частиц жидкости становится беспорядочным, струйка краски начинает размываться, отчего вся вода в трубке окрашивается.
Размывание струйки происходит вследствие образования вихрей и беспорядочного движения частиц. Однако у стенки, как и при ламинарном режиме, скорость остается равной нулю (рис.2). 
Рис. 2. Эпюры скоростей в трубе:
1 — при ламинарном течении; 2 — при турбулентном течении
При ламинарном течении жидкости в трубе эпюра скоростей имеет вид параболы; скорость в произвольной точке потока vr =  ,
,
где Δp – перепад давления по длине трубы; μ – динамическая вязкость; l – длина трубы; r0 – радиус трубы; r – радиус потока в точке определения скорости.
Максимальная скорость в центре поперечного сечения на оси трубы
vmax =  . (1)
. (1)
Расход жидкости через сечение трубы Q =  . (2)
. (2)
Средняя скорость vcр = Q/πr02 =  . (3)
. (3)
Сравнение формул (1) и (3) показывает, что при ламинарном течении средняя скорость в 2 раза меньше максимальной: vср = 0,5vmax.
При турбулентном течении жидкости в трубе можно говорить лишь о ее средней скорости. Характер течения зависит от средней скорости жидкости vср, диаметра трубопровода d, динамической вязкости μ и плотности жидкости ρ. Все эти факторы учитываются безразмерным комплексом, получившим название «число Рейнольдса»
Rе =  ,
,
где ν – кинематическая вязкость.
Физически число Рейнольдса характеризует отношение сил инерции и сил вязкости в потоке жидкости. Таким образом, режим движения жидкости для каждого конкретного случая зависит от числа Рейнольдса. Многочисленными опытами установлено предельное значение числа Рейнольдса, при превышении которого поток из ламинарного переходит в турбулентный. Это значение называется критическим числом Рейнольдса Rекр = 2320.
Средняя скорость, соответствующая ему, называется критической скоростью vкр =  .
.
Для потоков с сечением другой формы в качестве характеристики используют гидравлический радиус Rг или эквивалентный диаметр dэкв:
Rе = 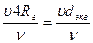 .
.
Число Рейнольдса является критерием, определяющим режим течения жидкости в трубах. При Rе‹2320 движение жидкости происходит при ламинарном режиме, при Rе›2320 – при турбулентном. При переходе от ламинарного движения к турбулентному и наоборот наблюдается промежуточный (переходный) режим (Rе = 2320…4000), при котором струйки имеют волнистый профиль, но не перемешиваются между собой.
Вполне развитое турбулентное течение в трубах устанавливается при Rе = 4000.
Пример 1.Определить число Рейнольдса и режим движения воды в водопроводной трубе d=30 мм, если расход воды Q=0,136 м3/с.Температура воды 100С .
Решение:
Живое сечение потока 
Средняя скорость движения воды в трубе 
Число Рейнольдса Rе =  .
.
uде ν – кинематическая вязкость (по табл. Определяем, что при температуре воды 10 0С ν = 1.31∙10-6 м2/с).
Отсюда Rе =  . Поскольку Rе›Rекр = 2320, движение воды будет турбулентным.
. Поскольку Rе›Rекр = 2320, движение воды будет турбулентным.
Пример 2.Применяемые в водоснабжении и канализации трубы имеют минимальный диаметр dmin=12 мм максимальный диаметр dmax=3500мм. Расчётные скорости движения воды в них 0.5 …4 м/с. Определить минимальное и максимальное числа Рейнольдса и режим течения воды в этих трубопроводах.
Решение:
Температура воды в системах водоснабжения может изменяться от 0 до 300С; согласно табл. Кинематическая вязкость при 00С ν0 =1.79∙10-6м2/с, а при 300С ν30 =0,81∙10-6м2/с.
Минимальное число Рейнольдса будет при d=dmin=0,012 м, v=0,5 м/с, ν= ν0:
Rеmin = =  =
= 
Максимальное число Рейнольдса будет при d=dmax=3,5 м, v=4 м/с, ν= ν30:
Rеmax = =  =
= 
Даже минимальное значение числа Рейнольдса больше Rекр = 2320, поэтому в трубопроводах систем водоснабжения и канализации режим движения воды всегда турбулентный.


|
из
5.00
|
Обсуждение в статье: Краткие теоретические сведения. Ламинарный и турбулентный режимы движения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

