Мультиколлениарности между факториальными признаками уравнения регрессии?

значение коэффициента парной корреляции равное 0,8

105.Как можно устранить мультиколлениарность между факториальными признаками уравнения регрессии?

исключить факториальный признак вызывающий мультиколлениарность;

106.Гетероскедастичность – это ….

явление, когда с изменением факториального признака (Х) демперсия случайной компоненты будет увеличиваться или уменьшаться, или изменяться по какому – либо другому закону;

107.Что понимается под дисперсией случайного члена уравнения регрессии?

характеризует тесноту связи функции Y с аргументами X_i , при условии, что прочие не включенные в уравнение регрессии аргументы этой функцией действуют корриляционно независимо от аргумента X_i;

108.Какой вид распределений случайнойго члена уравнения регрессии характерен для гомоскедастичного случая?

нормальное распределение кривой;

109. Гетероскедастичность случайного члена уравнения регрессии приводит :

с изменением факториального признака (Х) дисперсия случайной компоненты будет увеличиваться или уменьшаться, или измениться по какому – либо закону;

110. Возможный способ снижения влияния гетероскедастичность случайного члена уравнения регрессии на оценки параметров уравнения регрессии :

придать наблюдению с малой дисперсией больший вес, а наблюдениям с большой дисперсией меньший вес;

111. При выполнении теста ранговой корреляции Спирмена предполагается:

дисперсия случайной составляющей будет либо увеличиваться, либо уменьшаться по мере увеличения Х;

112. Для расчета коэффициента ранговой корреляции Спирмена необходимо упорядочить:

данные по Х и абсолютную величину e упорядочивают по возрастанию;

113. Расчет коэффициента ранговой корреляции Спирмена производится по формуле:

114. Тестовая статистика в тесте ранговой корреляции Спирмена определяется по формуле:

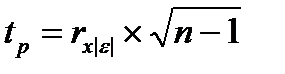
115. Согласно тесту ранговой корреляции Спирмена нулевая гипотеза об отсутствии гетероскедастичности случайного члена уравнения регрессии будет отклонена при уровне значимости в 5 % если тестовая статистика…

t_р > 1,96;

116. При проведении теста Голдфелда—Квандта предполагается…

Что стандартное отклонение σ_εi распределения вероятности ε_i пропорционально значению x в этом наблюдении;

117. Для выполнения теста Голдфелда-Квандта имеющиеся наблюдения:

упорядочиваются по возрастанию Х

118. В тесте Голдфелда-Квандта Нулевая гипотеза об отсутствии гетероскедостичности будет отклонена, если:

Fp>Fт

119. В тесте Голдфелда-Квандта рекомендуемое деление исходной выборки из 30 наблюдений на подвыборки составляет:

3 части

120. При проведении теста Глейзера предполагается:

что стандартное отклонение d_i связано с изменением факториального признака соотношением d_i=a’+b’*X_i^g

121. Для нахождения регрессионной зависимости, характеризующей изменение гетероскедастичности случайного члена уравнения регрессии в тесте Глейзера, используется регрессионное уравнение вида:

.

122. В тесте Глейзера нулевая гипотеза об отсутствии гетероскедастичности случайного члена уравнения регрессии будет отклонена, если в уравнении …

величина будет значимо отличаться от 0;

123. Для снижения влияния на оценки уравнения регрессии гетероскедастичности необходимо:

разделить коэффициенты уравнения регрессии на параметр, вызывающий гетероскедастичность.

124. Если наличие существенно гетероскедастичности и случайного члена уравнения регрессии ранговой корреляции Спирмена или тестом Голфелда Квандта, то для снижения влияния гетероскедастичнсти на эффективность оценок уравнения регрессии можно каждое наблюдение:

использовать вместо переменной , пропорциональной ;

125. Если наличие существенной гетероскедастичности случайного члена уравнения регрессии подтверждено тестом Глейзера то для снижения влияния гетероскедастичности на эффективность оценок уравнения регрессии необходимо:

в качестве Zi взять

126. Автокорреляция случайного члена уравнения регрессии – это…

зависимость одного члена уравнения от другого.

127. Автокорреляция случайного члена уравнения регрессии приводит к тому, что оценки уравнения регрессии становятся:

не эффективными, стандартные ошибки коэффициентов регрессии занижаются.

128. Причиной положительной автокорреляции случайного члена уравнения регрессии обычно является:

постоянная направленность воздействия не включенного в уравнение регрессии какого-либо фактора

129. Уравнение,отражающее авторегрессионную схему первого порядка для автокорреляции случайного члена, имеет вид:

;

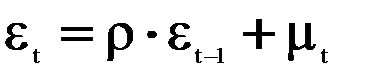130. Оценку коэффициента автокорреляции случайного члена уравнения регрессии из авторегрессионной схемы первого порядка можно осуществить по формуле:

;

131. Расчетное значение d – критерия статистики Дарбина - Уотсона определяется по формуле:

;

132. Значение d – критерия статистики Дарбина – Уотсона в больших выборках связано с коэффициентом автокорреляции случайного члена уравнения регрессии следующим соотношением:

.