 |
Главная |
Влияние автокорреляции на свойства оценок МНК
|
из
5.00
|
34. Тест серий. Статистика Дарбина – Уотсона.
Начнем с частного случая, в котором автокорреляция подчиняется авторегрессионной схеме первого порядка:
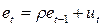 .
.
Это означает, что величина случайного члена в любом наблюдении равна его значению в предшествующем наблюдении (т. е. его значению в период t — 1), умноженному на ρ, плюс новый et,. Данная схема оказывается авторегрессионной, поскольку e определяется значениями этой же самой величины с запаздыванием, и схемой первого порядка. В этом простом случае максимальное запаздывание равно единице. Предполагается, что значение e в каждом наблюдении не зависит от его значений во всех других наблюдениях. Если ρ положительно, то автокорреляция положительная; если ρ отрицательно, то автокорреляция отрицательная. Если ρ = 0, то автокорреляции нет и третье условие Гаусса—Маркова удовлетворяется.
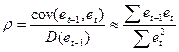
Широко известная статистика Дарбина—Уотсона (d илиDW) определяется следующим образом:

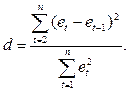
Можно показать, что в больших выборках
d→2-2ρ
Если автокорреляция отсутствует, то ρ= 0, и поэтому величина d должна быть близкой к двум. При наличии положительной автокорреляции величина d, вообще говоря, будет меньше двух; при отрицательной автокорреляции она, вообще говоря, будет превышать 2. Так как ρ должно находиться между значениями 1 и — 1, то d должно лежать между 0 и 4.
Критическое значение d при любом данном уровне значимости зависит, как можно предполагать, от числа объясняющих переменных в уравнении регрессии и от количества наблюдений в выборке. К сожалению, оно также зависит от конкретных значений, принимаемых объясняющими переменными. Поэтому невозможно составить таблицу с указанием точных критических значений для всех возможных выборок, как это можно сделать для t- и F-статистик; но можно вычислить верхнюю и нижнюю границы для критического значения d. Для положительной автокорреляции они обычно обозначаются как dv и dL.
На рис. данная ситуация представлена в виде схемы; стрелка указывает критический уровень d, который обозначается как d . Если бы мы знали значение dкрит, то могли бы сравнить с ним значение d, рассчитанное для нашей регрессии. Если бы оказалось, что d> dкрит, то мы не смогли бы отклонить нулевую гипотезу от отсутствии автокорреляции. В случае d<dкрит мы бы отклонили нулевую гипотезу и сделали вывод о наличии положительной автокорреляции

Тест Дарбина—Уотсона на автокорреляцию
(показана зона неопределенности в случае предполагаемой
положительной автокорреляции)
Вместе с тем мы знаем только, что dкриm находится где-то между dL и dU. Это предполагает наличие трех возможностей:
1. Величина d меньше, чем dL. В этом случае она будет также меньше, чем dKpum, и поэтому мы сделаем вывод о наличии положительной автокорреляции.
2. Величина d больше, чем dU. В этом случае она также больше критического уровня, и поэтому мы не сможем отклонить нулевую гипотезу.
3. Величина d находится между dL и dU. В этом случае она может быть больше или меньше критического уровня. Поскольку нельзя определить, которая из двух возможностей налицо, мы не можем ни отклонить, ни принять нулевую гипотезу.
В случаях 1 и 2 тест Дарбина—Уотсона дает определенный ответ, но случай 3 относится к зоне невозможности принятия решения, и изменить создавшееся положение нельзя.

. Тест Дарбина—Уотсона на автокорреляцию
(показана зона неопределенности в случае предполагаемой
отрицательной автокорреляции)
Проверка на отрицательную автокорреляцию проводится по аналогичной схеме, причем зона, содержащая критический уровень, расположена симметрично справа от 2. Так как отрицательная автокорреляция встречается относительно редко, предполагается, что при необходимости вы сами вычислите границы зоны на основе соответствующих значений для положительной автокорреляции при данном числе наблюдений и объясняющих переменных. Это достаточно легко сделать. Как показано на рис., величина (4 — dU) есть нижний предел, ниже которого признается отсутствие автокорреляции, а (4 - dL) — верхний предел, выше которого делается вывод о наличии отрицательной автокорреляции.
35. Способы противодействия автокореляции.
Возможно, вам удастся устранить автокорреляцию путем определения ответственного за нее фактора или факторов и соответствующего расширения уравнения регрессии. Когда такое возможно, это может оказаться наилучшим решением.
В других случаях процедура, которую следует принять, будет зависеть от характера зависимости между значениями случайного члена. В литературе наибольшее внимание уделяется так называемой авторегрессионной схеме первого порядка, так как она интуитивно правдоподобна, но для того, чтобы было целесообразным ее использование в более сложных моделях, оснований обычно не хватает. Вместе с тем если наблюдения проводятся ежеквартально или ежемесячно, могут оказаться более подходящими другие модели, но мы не будем их здесь рассматривать.
Если бы уравнение было правильной спецификацией для измерения величины случайного члена, то вы могли бы полностью устранить автокорреляцию, если бы знали величину ρ. Это будет продемонстрировано на примере уравнения регрессии, включающего только одну объясняющую переменную, однако при большем их числе действует тот же принцип. Предположим, что истинная модель задается выражением, так что наблюдения t и t — 1 формируются как
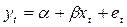
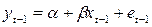
Теперь вычтем из первого уравнения второе, умноженное на ρ, и получим
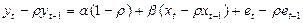 :
:
Обозначим:
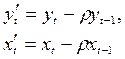
Это преобразование называется авторегрессионным, или преобразованием Бокса–Дженкинса.
Тогда преобразованное уравнение
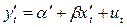
 где
где 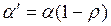 , не содержит автокорреляцию, поскольку ut независимы.
, не содержит автокорреляцию, поскольку ut независимы.
 Конечно, на практике величина ρ неизвестна, его оценка получается одновременно с оценками аир. Имеется несколько стандартных способов такого оценивания, и, вероятно, один или нескольких таких способов могут быть реализованы в имеющемся у вас регрессионном пакете.
Конечно, на практике величина ρ неизвестна, его оценка получается одновременно с оценками аир. Имеется несколько стандартных способов такого оценивания, и, вероятно, один или нескольких таких способов могут быть реализованы в имеющемся у вас регрессионном пакете.
Метод Кокрана—Оркатта представляет собой итеративный процесс, включающий следующие этапы.
1. Оценивается регрессия с исходными непреобразованными данными.
2. Вычисляются остатки.
3. Оценивается регрессионная зависимость et от еt-1, соответствующая
формуле и коэффициент при et-1 представляет собой оценку ρ  (поскольку D(et-1)≈D(et),в качестве альтернативной оценки ρ можно принять коэффициент автокорреляции первого порядка re-1,e)
(поскольку D(et-1)≈D(et),в качестве альтернативной оценки ρ можно принять коэффициент автокорреляции первого порядка re-1,e)
4. С этой оценкой ρ к преобразованному уравнению применяется МНК, который позволяет получить пересмотренные оценки α и β.
Повторно вычисляются остатки, и процесс возвращается к этапу 3.
Метод Хилдрета—Лу, также широко применяемый в регрессионных пакетах, основан на тех же самых принципах, но использует другой алгоритм вычислений. Здесь преобразованная регрессия оценивается для каждого значения ρ из определенного диапазона с заданным шагом внутри его. (Например, исследователь может задать диапазон от ρ = —1,00 до ρ= 1,00 с шагом 0,01.) Значение, которое дает минимальную стандартную ошибку для преобразованного уравнения, принимается в качестве оценки ρ, а коэффициенты регрессии определяются при оценивании уравнения с использованием этого значения.
|
из
5.00
|
Обсуждение в статье: Влияние автокорреляции на свойства оценок МНК |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

