Основные функции распределения

Функцией распределения F(x) случайной величины X называют F(x) = Р(P£ х). Ясно, что функция F(x) монотонно возрастает с ростом х (точнее сказать, не убывает, потому что могут существовать участки, на которых она постоянна). У дискретной случайной величины функция распреде­ления ступенчатая, она возрастает скачком в тех точках, вероятности которых положительны. Это точки разрыва F(x).

Биномиальное распределение — это одно из самых распространенных дискретных распределений, оно служит вероятностной моделью для многих явлений. Оно возникает в тех слу­чаях, когда нас интересует, сколько раз происходит некоторое событие в серии из определенного числа независимых наблюдений (опытов), выполняемых в одинаковых условиях.

Биноминальным называется закон распределения дискретной случайной величины X – число появлений события А в n одинаковых независимых испытаниях, в каждом из которых вероятность события A равна p, если вероятность P(X = k) появления события A равно k раз вычисляется по Формуле Бернулли:

Говорят, что дискретная случайная величина X – число появления события А в n одинаковых независимых испытаниях, в каждом из которых вероятность появления события A равно p, распределения по закону Пауссона, если число n очень велико, p очень мало и вероятность P(X = k) появления события A равно k раз вычисляется по Формуле Пауссона:

, где l = np.

Нормальное распределение относится к чи­слу наиболее распространенных и важных, оно часто используется для приближенного описания многих случайных явлений, например, для случайного отступления фактического размера изделия от номинально­го, рассеяния снарядов при артиллерийской стрельбе и во многих дру­гих ситуациях, в которых на интересующий нас результат воздействует большое количество независимых случайных факторов, среди которых нет сильно выделяющихся.

Случайная величина X имеет нормальное распре­деление вероятностей с параметрами а и σ² (краткое обозначе­ние: X ~ N(a, σ²)), если ее плотность распределения задается формулой:

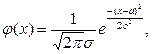- ∞ < x<∞.

Распределение хи-квадрат.. Пусть случайные величины X₁,X₂,…,Xn — незави­симы, и каждая из них имеет стандартное нормальное распределение N(0, 1). Говорят, что случайная величина χ_n², определенная как:

имеет распределение хи-квадрат с n степенями свободы. Для обозначе­ния этого распределения также обычно используется выражение χ_n²

F-pacnpe деление

Пусть Y₁,…,Y_n; X₁,…,X_n (где m, n — натураль­ные числа) обозначают независимые случайные величины, каждая из которых распределена по стандартному нормальному закону N(0, 1). Говорят, что случайная величина F, определенная как

имеет F-распределение с параметрами шип. Натуральные числа m, n называют числами степеней свободы.