 |
Главная |
Теоремы сложения и умножения вероятностей
|
из
5.00
|
Обобщим аксиому сложения вероятностей на произвольное число несовместных событий.
Теорема 1 (сложения вероятностей). Вероятность суммы произвольного числа  несовместных событий равна сумме вероятностей этих событий
несовместных событий равна сумме вероятностей этих событий
 .
.
Замечание. Аксиоматически теорема сложения вероятностей распространяется на случай бесконечного (счетного) числа событий
 .
.
Следствие 1. Сумма вероятностей событий, образующих полную группу, равна единице.
Следствие 2. Сумма вероятностей противоположных событий равна единице.
Чтобы сформулировать правило умножения вероятностей, введем понятие условной вероятности.
Определение. Условной вероятностью события  называется вероятность события
называется вероятность события  при условии, что другое событие
при условии, что другое событие  произошло (обозначается
произошло (обозначается  или
или  ).
).
Для иллюстрации последнего определения рассмотрим следующий пример.
Пример. Студент из 30 билетов успел выучить билеты с 1-го по 3-ий и с 28-го по 30-й. На экзамен он пришел одиннадцатым, и оказалось, что к его приходу остались только билеты с 1-го по 20-й (событие  ). Найти вероятность того, что студент получит выученный билет: а) без дополнительной информации о том, что событие
). Найти вероятность того, что студент получит выученный билет: а) без дополнительной информации о том, что событие  произошло; б) при дополнительной информации о том, что событие
произошло; б) при дополнительной информации о том, что событие  произошло.
произошло.
Решение. Пусть событие  - студент получил выученный билет. Согласно формуле (1) имеем для случая, когда дополнительная информация отсутствует (случай а) ):
- студент получил выученный билет. Согласно формуле (1) имеем для случая, когда дополнительная информация отсутствует (случай а) ):
 .
.
В случае наличия дополнительной информации (случай б) ) о том, что событие  уже произошло, число всех элементарных исходов испытания равно 20, а событие
уже произошло, число всех элементарных исходов испытания равно 20, а событие  наступает вместе с событием
наступает вместе с событием  в 3-х случаях. Следовательно, в случае б) естественно определить условную вероятность
в 3-х случаях. Следовательно, в случае б) естественно определить условную вероятность  события
события  при условии, что
при условии, что  произошло:
произошло:
 .
.
Сформулируем теперь четвертую аксиому, которая называется аксиомой умножения вероятностей.
40. Вероятность произведения (совмещения) двух событий равна произведению вероятности одного из них на условную вероятность другого:
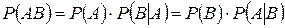 . (2)
. (2)
Прежде, чем рассматривать теорему умножения вероятностей, введем понятие независимых и зависимых событий.
Определение. События  и
и  называются независимыми, если условная вероятность одного из них, при условии, что второе произошло, равна безусловной (исходной) вероятности первого:
называются независимыми, если условная вероятность одного из них, при условии, что второе произошло, равна безусловной (исходной) вероятности первого:
 или
или  ,
,
другими словами, вероятность события  не зависит от того, произошло событие
не зависит от того, произошло событие  или нет (и наоборот).
или нет (и наоборот).
Замечание. Для независимых событий, таким образом справедливо соотношение:

Пример. В урне находятся 3 белых и 4 черных шара. Из урны наудачу берут один шар, затем взятый шар возвращают в урну и испытание повторяют. Найти вероятность появления белого шара при первом испытании и при втором испытании.
Решение. Пусть событие  - появление белого шара при первом испытании, событие
- появление белого шара при первом испытании, событие  - появление белого шара при втором испытании. Очевидно, что вероятность события
- появление белого шара при втором испытании. Очевидно, что вероятность события  (
(  ) не зависит от результата первого испытания. Таким образом, событие
) не зависит от результата первого испытания. Таким образом, событие  не зависит от события
не зависит от события  (
(  ).
).
Замечание. Если события  и
и  независимы, то независимы также события:
независимы, то независимы также события:  и
и  ,
,  и
и  ,
,  и
и  .
.
Теорема 2 (умножения вероятностей). Вероятность произведения, или совместного появления, нескольких событий равна произведению вероятности одного из них на условные вероятности остальных событий, вычисленные в предположении, что все предшествующие события имели место:
 .(3)
.(3)
Замечание. Теорема может быть доказана методом математической индукции аналогично теореме 1.
Определение. События  называются независимыми в совокупности, если каждое из них не зависит от остальных и их произведений.
называются независимыми в совокупности, если каждое из них не зависит от остальных и их произведений.
Замечание. Для событий  , независимых в совокупности, формула (3) принимает вид:
, независимых в совокупности, формула (3) принимает вид:
 . (4)
. (4)
Пример. В двух ящиках, содержащих по 10 деталей, находятся стандартные детали: 5 в первом и 7 во втором. Из каждого ящика вынимают по одной детали. Найти вероятность того, что две вынутые детали окажутся стандартными.
Решение. Пусть событие  - из 1-го ящика вынули стандартную деталь, вероятность этого события равна
- из 1-го ящика вынули стандартную деталь, вероятность этого события равна  ; событие
; событие  - из 2-го ящика вынули стандартную деталь, вероятность этого события равна
- из 2-го ящика вынули стандартную деталь, вероятность этого события равна  ; событие
; событие  - две вынутые детали стандартны (и 1-я и 2-я).
- две вынутые детали стандартны (и 1-я и 2-я).
Так как 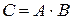 и события
и события  и
и  являются независимыми, то
являются независимыми, то
 .
.
Пример.В ящике 6 белых и 8 черных шаров, из ящика вынули два шара, не возвращая вынутый шар в ящик. Найти вероятность того, что оба шара белые.
Решение. Пусть событие  - вынутый первым шар белый, вероятность этого события равна
- вынутый первым шар белый, вероятность этого события равна 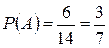 ; событие
; событие  - вынутый вторым шар белый (при условии, что белым был первый шар), вероятность этого события равна
- вынутый вторым шар белый (при условии, что белым был первый шар), вероятность этого события равна  ; событие
; событие  - два шара белые (и 1-й и 2-й).
- два шара белые (и 1-й и 2-й).
События  и
и  зависимые,
зависимые, 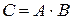 , поэтому
, поэтому
 .
.
Теорема умножения вместе с теоремой сложения вероятностей для несовместных событий позволяют доказать теорему сложения вероятностей совместных событий.
Теорема 3 (сложения вероятностей для совместных событий). Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
 .
.
Для исключения громоздких вычислений переходят к противоположному событию и записывают теорему в следующей формулировке.
Теорема о вероятности появления хотя бы одного из n независимых событий. Вероятность появления хотя бы одного из n независимых событий равна разности между единицей и произведением вероятностей событий, противоположных данным:
 .
.
Пример.Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75, для второго 0,8, для третьего – 0,9. Найти вероятность того, что в цель попадет хотя бы один стрелок.
Решение. Пусть событие  - первый стрелок попал в цель,
- первый стрелок попал в цель, 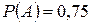 ,
,  ; событие B – второй стрелок попал в цель,
; событие B – второй стрелок попал в цель,  ,
,  ; событие С – третий стрелок попал в цель,
; событие С – третий стрелок попал в цель,  ,
, 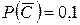 .
.
Событие D – хотя бы один стрелок попал в цель.
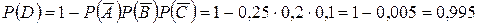 .
.
|
из
5.00
|
Обсуждение в статье: Теоремы сложения и умножения вероятностей |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

