Основные теоремы линейного программирования

Для обоснования методов решения задач линейного программирования сформулируем ряд важнейших теорем, опуская их аналитические доказательства. Уяснить смысл каждой из теорем поможет понятие о геометрической интерпретации решения ЗЛП, данное в предыдущем подразделе.

Однако сначала напомним о некоторых понятиях, важных с точки зрения дальнейшего разговора.

Любые m переменных системы m линейных уравнений с n переменными (m < n) называются основными, если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные m-n переменных называются неосновными (или свободными).

Базисным решением системы m линейных уравнений c n переменными (m < n) называется всякое ее решение, в котором все неосновные переменные имеют нулевые значения.

Теорема 1. Множество всех допустимых решений системы ограничений задачи линейного программирования является выпуклым.

В частном случае, когда в систему ограничений входят только две переменные x1 и x2, это множество можно изобразить на плоскости. Так как речь идет о допустимых решениях (x1, x2 ? 0), то соответствующее множество будет располагаться в первой четверти декартовой системы координат. Это множество может быть замкнутым (многоугольник), незамкнутым (неограниченная многогранная область), состоять из единственной точки и, наконец, система ограничений-неравенств может быть противоречивой.

Теорема 2. Если задача линейного программирования имеет оптимальное решение, то оно совпадает с одной (двумя) из угловых точек множества допустимых решений.

Из теоремы 2 можно сделать вывод о том, что единственность оптимального решения может нарушаться, причем, если решение не единственное, то таких оптимальных решений будет бесчисленное множество (все точки отрезка, соединяющего соответствующие угловые точки).

Теорема 3. Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка области допустимых решений, и наоборот.

Следствием из теорем 2 и 3 является утверждение о том, что оптимальное решение (оптимальные решения) задачи линейного программирования, заданной (или приведенной) ограничениями-уравнениями, совпадает с допустимым базисным решением (допустимыми базисными решениями) системы ограничений.

Таким образом, оптимальное решение ЗЛП следует искать среди конечного числа допустимых базисных решений.

 

Вопрос 10:Построение исходного плана.

Построение исходного опорного плана (метод северо-западного угла)

Для начала решения транспортной задачи необходимо иметь какой-то исходный опорный план, то есть оказаться в какой-то вершине допустимой области. Приведем конструктивный прием построения такого опорного плана, получивший название "метод северо-западного угла".

Итак, пусть имеется m складов с запасами

и n пунктов

 

потребления с потребностями .

Пусть запасы и потребности

 

сбалансированы, то есть .

Представим это в виде таблицы,

			...

где в столбце справа указаны запасы, в строке снизу  потребности, а пустые клетки оставлены для будущего плана перевозок.

Начнем заполнение с клетки, расположенной вверху слева, то есть с "северо-западного угла". Вместо впишем число . Возможны два варианта.

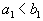1. , то есть . Тогда, запланировав перевозку из первого склада в первый пункт потребления в объеме мы полностью опустошим первый склад и там ничего не останется. Поэтому все остальные перевозки из первого склада могут быть только нулевые.

Ну, а потребность в первом пункте потребления останется в объеме . Наша таблица примет вид:

			...
			...

Обратите внимание на то, что оставшаяся незаполненной часть таблицы вновь по структуре та же, что и исходная таблица, только в ней на одну строку меньше.

 

2. , то есть . Тогда, запланировав перевозку из первого склада в первый пункт потребления в объеме , мы полностью удовлетворим его потребности. Перевозить туда больше будет ничего не надо, поэтому остальные перевозки туда будут равны нулю.

Ну, а в первом складе еще останется запасов продукта. Наша таблица примет вид:

			...

Обратите внимание на то, что оставшаяся незаполненной часть таблицы вновь по структуре та же, что и исходная таблица, только в ней на один столбец меньше.

Ну, а дальше все можно повторить, продолжая заполнять оставшуюся часть таблицы перевозок начиная с левого верхнего, "северо-западного" угла, пока не будут исчерпаны запасы всех складов и не удовлетворены потребности всех пунктов потребления.

У нас всего в таблице m строк и n столбцов. Каждый раз исчезает, как минимум, либо строка, либо столбец (могут исчезнуть сразу и строка, и столбец, если запасы какого-то подмножества складов полностью удовлетворят потребности какого-то подмножества пунктов потребления). Однако при последней перевозке исчезает сразу и последняя строка, и последний столбец. Поэтому получающийся план перевозок содержит не

более

компонент.

Мы не будем доказывать, что план, полученный методом северо-западного угла, является опорным. Заметим лишь, что если получающийся план содержит ровно компоненту, то он называется невырожденным. Если число положительных компонент плана перевозок меньше , то он называется вырожденным.

Рассмотрим два примера. С целью экономии места, вся таблица не переписывается, а лишь приписываются последние строки и столбцы.

Пример 1

Пусть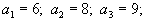

				В данном случае число
				складов m =3, число пунктов
				потребления n =4, так что
				m+n-1=6. Получившийся
				опорный план содержит ровно
				6 компонент, и поэтому являет-
				ся невырожденным.

Пример 2

Пусть Аналогичная процедура приводит к таблице, изображенной ниже.

В этом случае получившийся опорный план имеет всего 5 компонент, то есть является вырожденным. Это

				В данном случае число скла-
				дов m =3, число пунктов потре-
				бления n =4, так что m+n-1=6.
				Получившийся опорный план
				содержит 5 компонент, и поэтому
				является вырожденным.

произошло потому, что запасы складов и полностью удовлетворили потребности пунктов потребления и и поэтому в тот момент, когда эти сбалансированные потребности удовлетворились ( ), обнулились сразу и строка, и столбец.

Ниже вся теория будет строится для случая, когда все опорные планы невырожденные, то есть все они имеют компоненту. Как бороться с явлением вырождения, которое в транспортных задачах встречается достаточно часто  будет рассказано в самом конце.

 

Вопрос 11:Симплексные таблицы. Последовательное улучшение плана. Связь оценок свободных неизвестных с приращением целевой функции.

симплекс-таблица представляет собой расширенную матрицу системы ограничений с некоторыми дополнительными столбцами и строками. Рассмотрим пример симплекс таблицы для следующей задачи:

Найти значения переменных x₁...x₅, при которых функция:

Q =

x1

+

x2

+

принимает максимальноезначение, при условии следующих ограничений :

x1

+

x2

+

x3

=

(1)

x1

+

x2

+

x4

=

(2)

-

x2

+

x5

=

(3)

x₁, x₂, x₃, x₄, x₅ ≥ 0

Симплекс таблица имеет следующий вид:

БП	x1	x2	x3	x4	x5	Решение	Отношение
x3							/ =
x4							/ =
x5		-1					--
Q						-2	--

 

Самая верхняя строка - чисто информационная, в ней указывается назначение столбцов. Столбец "БП" также информационный, каждая клетка этого столбца содержит имя переменной, являющейся базисной в соответствующем уравнении системы ограничений. В нашем примере, в первом уравнении, базисной переменной является переменная X₃, во втором X₄, в третьем X₅.

Столбцы X1...X₅ содержат коэффициенты при соответствующих переменных в уравнениях системы ограничений (каждому уравнению соответствует отдельная строка). В столбец "Решение" изначально записываются свободные члены соответствующих уравнений. Они же показывают значения базисных переменных для текущегого решения, отображаемого симплекс-таблицей, на некотором шаге (итерации) решения задачи.

Коэффициенты целевой функции отражаются в симплекс-таблице в строке "Q", свободный член, как и в случае с уравнениями системы ограничений, изначально записывается в столбец "Решение". Он же одновременно является значением целевой функции, но записанный с противоположным знаком (это удобно для симплекс-метода). В нашем примере показанная симплекс-таблица соответствует некоторому решению при котором переменные X₃, X₄, X₅ равны соответственно 64, 70, 18 (см. столбец "Решение"), а остальные перемнные равны нулю. Значение целевой функции "Q" при этом равно двум (что несложно проверить подставив значения переменных в выражение для целевой функции).

В нашем примере свободный член равен -2 (минус два) т.к. в записи целевой функции он записан вместе с переменными по одну сторону от знака равенства, а свободные члены в уравнениях системы ограничений по другую. Поэтому перед записью в таблицу его необходимо перенести вправо от знака равенства.

Строка "Q" в данном примере выделена желтым цветом, это значит, что по ней будет приниматься решение относительно выбора разрешающего столбца (иногда его называют направляющим). Разрешающий столбец соответствует переменной, которая будет введена в базис (в список базисных переменных) на следующей итерации решения задачи. Цель подобной замены базиса - улучшение значения целевой функции. Критерием выбора разрешающего столбца является максимальный положительный коэффициент в строке "Q", при решении задачи на максимум, или минимальный отрицательный, при решении задачи на минимум. Если после очередной итерации в строке не окажется положительных (при максимизации), или отрицательных (при минимизации) коэффициентов, то оптимальное решение достигнуто. В нашем примере разрешающий столбец выбран по коэффициенту 7 (максимальный положительный т.к. задача на максимум), он соответствует переменной X₂, именно она будет введена в базис на следующей итерации. Числа стоящие в направляющем столбце окрашиваются красным цветом.

Красным цветом также окрашивается и разрешающая (направляющая) строка, она соответствует переменной которая будет выведена из базиса (списка базисных переменных) на следующей итерации. Для ее определения рассчитывается и заполняется столбец "Отношение". Его элементы представляют собой отношения элементов столбца "Решение" к соответсвующим элементам направляющего столбца (кроме строки "Q"). Выбор разрешающей строки производится по минимальному значению из всех отношений. Важно то, что данные отношения рассчитываются только для положительных элементов направляющего столбца. Если на некоторой итерации в направляющем столбце положительных коэффициентов не окажется, то целевая функция исходной задачи неограничена, задача не имеет решения.
В нашем примере направляющая строка выбрана по минимальному отношению 16, она соответствует базисной переменной X₃, именно она будет выведена из базиса на следующей итерации (ее место займет X₂)

 

Вторая часть вопроса:

Описываемый здесь метод основан на симплексном переходе от одного базиса к другому. Метод разработан для решения задач линейного программирования, записанной в форме (1.1) -(1.3). Для записи ограничений (1.2) используем формулу (1.4).

Считается, что найден базис P₁,P₂,…,P_m, обозначаемый

(P₁,P₂,…,P_m ) = В (3.1) такой, что в разложении

P₀ = ξ₁₀P₁ + ξ₂₀P₂ +…+ ξ_m0P_m (3.2)

Коэффициенты ξ_i0 ≥ 0 ,i=1,…,m.

Соглашение о том, что исходный базис В составляет первые m столбцов матрицы А, не ограничивает общности рассуждений, так как этого можно добиться перенумерацией неизвестных.

Согласно определению 2 n-мерный вектор

х₀ = (ξ₁₀, ξ₂₀,…,ξ_m0,0,…,0)^t

является опорным планом, соответствующим базису (3.1).

Конечной целью решения задачи линейного программирования является нахождение минимума линейной формы. Поэтому симплексный переход от базиса В к новому базису В’ целесообразно осуществлять так, чтобы для опорного плана x' , соответствующего базису B’ , выполнялось неравенство С^tx₀ ≥ С^tx’.В этом случае говорят, что план x' лучше плана x₀. Улучшать план можно с помощью различных алгоритмов. Один из них и описывается в настоящем параграфе.

Пусть

P_k =ξ_1kP_k+ξ_2kP₂+...+ξ_mkP_m , k=0,1,...,m (3.3)

При k=0 равенство (3.3) совпадает с (3.2). Обозначим

Z_k=ξ_1kC₁+ξ_2kC₂+...+ξ_mkC_m , k=0,1,...,n (3.4)

Заметим, что z₀=C^tx₀ , т.е. z₀, является значением линейной формы C^tx на опорном плане x₀.

Все исходные данные сведем в таблицу, называемую симплексной (см.табл.3.1). В симплексной таблице первые два столбца

Таблица 3.1

Базис В	Сбаз	С0=0	С1	C2...	Cs...	Cm...	Cj...	Ck...	Cn
B-1P0	B-1P1	B-1P2...	B-1Ps...	B-1Pm...	B-1Pj...	B-1Pk...	B-1Pn
P1	C1	ξ10		0...	0...	0...	ξ1j...	ξ1k...	ξ1n
P2	C2	ξ20		1...	0...	0...	ξ2j...	ξ2k...	ξ2n
...	...	...	...	...	...	...	...	...	...
Ps	Cs	ξs0		0...	1...	0...	ξsj...	ξsk...	ξsn
...	...	...	...	...	...	...	...	...	...
Pm	Cm	ξm0		0...	0...	1...	ξmj...	ξmk...	ξmn
∆k = zk-ck	z0		0...	0...	0...	zj-cj...	zk-ck...	zn-cn

и первые две строки назовем окаймляющими. Остальные элементы составляют основную таблицу. Строкам таблицы приписываются номера от 1 до m+1, столбцам от 1 до n. В столбец окаймления “базис” записываются векторы базиса или их номеры. В столбец С_баз записываются коэффициенты C_i линейной формы C^tx с номерами, соответствующими номерам базисных векторов. В первой окаймляющей строке выписываются все коэффициенты линейной формы, для единообразия дальнейших вычислений в нулевом столбце можно записать C₀=0. В к-ом (к=0,...,n) столбце стоят коэффициенты разложения вектора Р_к по базису В, точнее ξ_sk – коэффициент при векторе Р_к по базису В. Числа ∆_k = z_k-c_k , стоящие в m+1-ой строке, называются оценками, при этом ∆₀=z₀=C_баз B^-1P₀= C^tx₀. Заметим, что z_k по определению (3.4) является скалярным произведением столбца С_баз на столбец B^-1P_к. В связи с этим

∆_k=С^t_баз B^-1P_к-С_к , k=0,1,...,n. (3.5)

Заметим, что если уравнение (1.4) умножить слева на B^-1, то получим уравнение

B^-1P₀ = ξ₁ B^-1P₁ + ξ₂ B^-1P₂ + ξ_n B^-1P_n , равносильное уравнению (1.4). Таким образом, в симплексной таблице 3.1 записана в преображенном виде расширенная матрица системы (1.2).

Теорема 1. Пусть для базиса (3.1) выполняются неравенства ξ_i0 ≥ 0, i=1,...,m и z_k - c_k ≤ 0,k=1,...,n. Тогда опорный план х₀ , соответствующий базису (3.1) оптимален.

Доказательство. Пусть y=(η₁,η₂,...,η_n)^t произвольный план задачи (1.1)-(1.3). Тогда η_к ≥ 0, к=1,...,n и ∑η_кР_к = Р₀ (сумма от к=1 до n). Отсюда Р₀ = ∑∑η_кξ_jkP_k (сумма от j=1 до m, сумма от к=1 до n)в силу (3.3). Сравнивая это равенство с (3.2), в силу единственности разложения вектора Р₀ по базису В находим

ξ_j0 = ∑ η_kξ_jk (сумма от к=1 до n) используя это равенство, а также неравенства z_k ≤ c_k , k=1,...,n и равенство (3.4), находим С^ty = ∑ c_kη_k ≥ ∑z_kη_k (сумма от к=1 до n)= = ∑∑ξ_jkη_kc_j (сумма от j=1 до m, сумма от к=1 до n) = ∑c_jξ_j0 (сумма от j=1 до m) =С^tx₀.

Но это неравенство, в силу произвольности плана y, и означает, что опорный план х₀ оптимален. Теорема доказана.

Итак, если все оценки неположительные, то задача (1.1)-(1.3) решена. Пусть далее базис В таков, что ему соответствует опорный план х₀ и среди оценок ∆_k, k=1,...,n есть положительные. В этом случае могут возникнуть две существенно различные ситуации. Первая из них характеризуется следующей теоремой.

Теорема 2. Пусть для базиса (3.1) выполняется неравенства ξ_i0 ≥ 0 , i=1,…,m. Если для какого-либо j выполняется неравенство Δ_j > 0, но ξ_ij ≤ 0 для всех i=1,…,m, то линейная форма С^tх неограничена снизу.

Доказательство. Вычитая из равенства (3.2) равенство (3.3) при k = j, умноженное на произвольное положительное число θ, получим P₀ = ∑(ξ_i0 - θξ_ij)Pi + θP_j (сумма от i=1 до m). Это равенство показывает, что n – мерный вектор х’ = (ξ₁₀ – θξ_1j,…, ξ_m0- θξ_mj, 0,…, 0, θ,…,0)^t, где θ является j- ой координатой, удовлетворяет условию (1.4). Так как ξ_i0 ≥ 0, ξ_ij ≤ 0, для любого i, то х’ ≥ 0 и, следовательно, х’ является планом задачи (1.1)-(1.3). Тогда из равенства С^tx’= ∑C_i(ξ_i0 - θξ_ij) + θC_j = С^tx₀ - θΔ_j (сумма от i=1 до m), справедливого для любого θ > 0, следует неограниченность линейной формы С^tx снизу. Теорема доказана.

Итак, в ситуации, описанной в теореме 2, решение задачи линейного программирования заканчивается, так как минимум линейной формы С^tx становится известным, он равен -∞.

Пусть таблица 3 такова, что для тех j, для которых Δ_j > 0, выполняется неравенство ξ_ij > 0, хотя бы для одного i. В этом случае делается симплексный переход к новому базису. При этом ставится цель – для опорного плана, соответствующего новому базису, значение линейной формы не должно быть больше, чем при старом плане. Будет показано, что через конечное число таких переходов возникнет одна из ситуаций, описанных теоремами 1или 2.

Итак, опишем процедуру симплексного перехода к новому базису с уменьшением линейной формы С^tx. Пусть исходным является базис (3.1) и пусть новый базис образуют векторы

(P₁,…,P_s-1,P_j,P_s+1,…,P_m) = B’ , j > m. (3.6). Согласно лемме 2 ξ_ij (см. формулу (3.3) при k = j) отличен от нуля. В силу леммы 3 разложение любого вектора P_k по базису (3.6) имеет вид

P_k = ∑(ξ_ik – (ξ_sk/ξ_sj)ξ_ij)P_i + (ξ_sk/ξ_sj)P_j (сумма от i≠s до m), k=0,1,…,n. (3.7)

Эту формулу, впрочем, можно получить непосредственно, если записать равенство (3.3) при k = j, найти из него P_s и найденное для P_s выражение подставить в (3.3).

Тогда новое значение z’_k, являющееся скалярным произведением столбцов С_баз и к-го новой симплексной таблицы, определится равенством

z’_k = ∑(ξ_ik – (ξ_sk/ξ_sj)ξ_ij)C_i + (ξ_sk/ξ_sj)C_j (сумма от i≠s до m), k = 0,1,…,n. (3.8)

Вычитая, наконец, С_к из обеих частей равенства (3.8) и считая С₀=0, получим формулы пересчета для оценок ∆’_k= ∆_k – (ξ_sk/ξ_sj) ∆_j , k=0,1,…,n (3.9)

Формулы (3.9) показывают, что оценки ∆_к пересчитываются по тем же правилам исключения (2.10), по каким пересчитываются и координаты векторов Р_к.

Проведем теперь анализ, который позволит установить правило выбора вводящегося в базис вектора P_j и выводящегося из базиса (3.1) вектора P_s. Для этого обратимся к равенствам (3.7) и (3.9) при k = 0. Обозначим θ_j = ξ_s0/ξ_sj в силу формулы (3.9) при k = 0, новое значение ∆₀ линейной формы С^tх может быть меньше старого значения ∆₀, если θ_j∆_j ≥ 0 (3.10).

В силу формулы (3.7) при k = 0 вектор x’ = (ξ’₁₀, ξ’₂₀,…, ξ’_n0), где

ξ_i0 - θ_jξ_ij , i=1,…,s-1,s+1,…m,

ξ’_io = θ_j , i = j (3.11)

0 в остальных случаях,

удовлетворяет ограничениям (1.4). Чтобы вектор х’ был планом, необходимо, чтобы выполнялись неравенства ξ’_i0 ≥ 0, i=1,…,n.

В частности, чтобы обеспечить неравенство ξ’_i0 = θ_i ≥ 0 в любых задачах, необходимо выбирать ведущий элемент ξ_sj > 0. По тем же причинам из (3.10) следует, что j надо выбирать так, чтобы было Δ_j > 0.

Найдем, наконец, условия, при которых будут неотрицательными ξ’_i0 при i ≠ s. Так как ξ_i0 ≥ 0, θ_j ≥ 0 то неравенства ξ_i0 – θ_jξ_ij ≥ 0 выполняются для тех i, для которых ξ_ij ≤ 0. Пусть I ={i| ξ_ij > 0}. Чтобы выполнялись неравенства ξ_i0 - θ_jξ_ij ≥ 0 для всех i I, должны выполняться неравенства θ_j ≤ ξ_i0/ξ_ij для любого i I. Так как s I и θ_j = ξ_s0/ξ_sj ,то θ_j = min ξ_i0/ξ_ij. Это равенство и определяет правило выбора выводящегося из базиса вектора. Именно в качестве индекса s нужно выбирать тот, для которого достигается минимум отношений ξ_i0/ξ_ij при i I.

В результате такого выбора индексов j и s план x’ с координатами (3.11) будет опорным, так как ненулевым координатам плана x’ соответствует линейно-независимые векторы (3.6).

Полученный результат сформулируем в виде теоремы.

Теорема 3. Пусть для базиса (3.1), которому соответствует опорный план x₀, выполняются неравенства Δ_j > 0 для некоторого j и ξ_ij > 0 хотя бы для одного i. Тогда базису (3.6), где s oопределяется равенством θ_j = ξ_s0/ξ_sj = min ξ_i0/ξ_ij, (i| ξ_ij > 0), (3.13) соответствует опорный планx’, для которого C^tx’ ≤ C^tx₀, при этом С^tx’ < C^tx₀, если ξ_{s0 ¹} 0.

Теоремой 3 завершается формулировка принципов построения нового опорного плана x’ такого, что С^tx’ ≤ C^tx₀.Эти принципы можно реализовать с помощью различных алгоритмов. Следующий алгоритм называется симплексным методом илиметодом последовательного улучшения плана.

Симплексный метод. Пусть выполнены следующие два условия:

А) выбран базис (3.1) такой, что в разложении (3.2) все ξ_i0≥ 0,

Б) построена соответствующая этому базису симплексная таблица 3.1.

1. Если Δ_j ≤ 0 для всех j=1,…,n, то задача решена и опорный план х₀, соответствующий базису (3.1), является оптимальным. В противном случае переходим к пункту 2.

2. Просматриваются столбцы B^-1P_j для тех j, для которых

Δ_j = z_j – c_j > 0. Если хотя бы в одном из таких столбцов ξ_ij ≤ 0 для всех i=1,…,m, то решение задачи прекращается - линейная форма не ограничена снизу. В противном случае выбирается любое j, для которого Δ_j > 0. Вектор Р_j будет вводиться в базис.

3. Выбирается минимальное из отношений ξ_i0/ξ_ij для тех i, для которых ξ_ij > 0. Пусть этот минимум достигается при i = s. Тогда вектор P_s выводится из базиса. Обозначим ξ_s0/ξ_sj = θ_j.

4. В окаймляющих столбцах "базис" и С_баз таблицы 3.1 вектор P_s и число С_s заменяются, соответственно, на P_j и C_j.

5. Элемент ξ_sj выбирается за ведущий и в таблице 3.1 производится процесс исключения элементов j-го столбца, в том числе и элемента Δ_j, по одному из алгоритмов 1-3 исключений из §2 (см. табл. 2.1 и 2.2). Для вновь полученной симплексной таблицы процесс повторяется с пункта 1.

Замечание. Легко понять, что при решении задачи максимизации С^tх при ограничениях (1.2), (1.3) можно использовать этот же алгоритм с той разницей, что в базис нужно вводить вектор P_j, для которого Δ_j < 0 и останавливать счет, если Δ_j ≥ 0 для всех j=1,…,n. При этом линейная форма окажется неограниченной сверху, если хотя бы для одного j выполняются одновременно неравенства Δ_j < 0, ξ_ij ≤ 0, i=1,…,m.

 

Вопрос 12.