 |
Главная |
Свойства выпуклых множеств
|
из
5.00
|
Математическое программирование
Вопрос 8: Выпуклые множества. Выпуклая линейная комбинация точек.
Выпуклое множество - подмножество евклидова пространства содержащей отрезок, соединяющий любые какие две точки этой множества.
Определение
Другими словами, множество  называется выпуклой, если:
называется выпуклой, если:
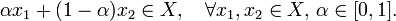
То есть, если множество X вместе с любыми двумя точками, которые принадлежат этому множеству, содержит отрезок, их соединяющий:
 .
.
В пространстве  выпуклыми множествами будут прямая, полупрямой, отрезок, интервал, одноточечный множество.
выпуклыми множествами будут прямая, полупрямой, отрезок, интервал, одноточечный множество.
В пространстве  выпуклым будет само пространство, любое его линейный подпространство, шар, отрезок, одноточечный множество. Также, выпуклыми будут такие множества:
выпуклым будет само пространство, любое его линейный подпространство, шар, отрезок, одноточечный множество. Также, выпуклыми будут такие множества:
- прямая
 , проходящая через точку x 0 в направлении вектора h :
, проходящая через точку x 0 в направлении вектора h :
 ;
;
- луч
 , выходящий из точки x 0 в направлении вектора h :
, выходящий из точки x 0 в направлении вектора h :
 ;
;
- гиперплоскости H p? с нормалью p :
 ;
;
- полупространства на которые гиперплоскости разделяет пространство:
 ,
,
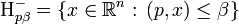 .
.
Все перечисленные множества (кроме пули ) является частным случаем выпуклой множества полиэдры.
Свойства выпуклых множеств
- Пересечение выпуклых множеств является выпуклым.
- Линейная комбинация точек выпуклой множества выпуклая.
- Выпуклая множество содержит любую выпуклую комбинацию своих точек.
- Любую точку n -мерного евклидова пространства с выпуклой оболочки множества можно представить как выпуклую комбинацию не более n +1 точек этого множества
Рассмотрим n - мерное евклидово пространство  и пусть
и пусть  точка в этом пространстве.
точка в этом пространстве.
Рассмотрим две точки  и
и  , принадлежащие
, принадлежащие  .Множество точек
.Множество точек  , которые могут быть представлены в виде
, которые могут быть представлены в виде

(в координатах это записывается так:
 ,
,
называется выпуклой комбинациейточек  и и 
| , или |
отрезком, соединяющим точки  и
и  . Сами точки
. Сами точки  и
и  называются концами отрезка. В случаях n =2 и n =3 это отрезок в обычном понимании этого слова на плоскости или в пространстве (см. рис. 12). Заметим, что при =0
называются концами отрезка. В случаях n =2 и n =3 это отрезок в обычном понимании этого слова на плоскости или в пространстве (см. рис. 12). Заметим, что при =0 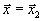 , а при =1
, а при =1  , т.е. при =0 и =1 получаются концы отрезка.
, т.е. при =0 и =1 получаются концы отрезка.

Пусть в 
| заданы k точек 
| . Точка |
 ,
,
где все  и
и 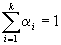 называется выпуклой комбинациейточек
называется выпуклой комбинациейточек  .
.
Пусть  есть некоторая область в пространстве
есть некоторая область в пространстве  (другими словами,
(другими словами,
G есть некоторое множество точек из 
| ). |
Определение. Множество (область)  называется выпуклым, если из того, что
называется выпуклым, если из того, что  и
и  следует, что
следует, что  для [0,1]. Другими словами, G выпуклое множество, если оно, вместе с любыми двумя своими точками, содержит в себе отрезок, соединяющий эти точки.
для [0,1]. Другими словами, G выпуклое множество, если оно, вместе с любыми двумя своими точками, содержит в себе отрезок, соединяющий эти точки.

На этих рисунках "а" и "б" - выпуклые множества, а "в" не является выпуклым множеством, так как в нём есть такая пара точек, что соединяющий их отрезок не весь принадлежит этому множеству.
Теорема 1. Пусть G выпуклое множество. Тогда любая выпуклая комбинация точек, принадлежащих этому множеству, также принадлежит этому множеству.
Доказательство
Пусть 
| точки, принадлежащие множеству G . |
Докажем теорему методом математической индукции. При k =2 теорема верна, так как она просто переходит в определение выпуклого множества.
Пусть теорема верна для некоторого k. Возьмём точку  и рассмотрим выпуклую комбинацию
и рассмотрим выпуклую комбинацию
 ,
,
где все 
| и 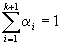 . .
|
Представим 
| в виде |

Но коэффициенты 
| и |
 ,
,
и, раз мы считаем, что для k теорема верна, точка
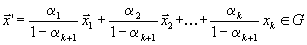 .
.
Но тогда  является выпуклой комбинацией точек
является выпуклой комбинацией точек 
и 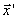 и, по определению выпуклого множества, и, по определению выпуклого множества,  . .
|
Теорема доказана.
Теорема 2. Допустимая область задачи линейного программирования является выпуклым множеством.
Доказательство.
1. В стандартной форме в матричных обозначениях допустимая область G определяется условием

Пусть 
| и 
| принадлежат G , т.е. |

Но тогда для 
| имеем |



т.е. x принадлежит G и, следовательно, выпукло.
2. В канонической формеобласть G определена условиями
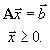
Пусть  и
и  принадлежат G, т.е.
принадлежат G, т.е.
 .
.
Но тогда для 
| имеем |
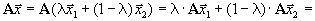


т.е. и, следовательно, G выпукло. Теорема доказана.
Таким образом, допустимая область в задаче линейного программирования является выпуклым множеством. По аналогии с двумерным или трехмерным случаями, при любом n эту область называют выпуклым
многогранникомв n - мерном пространстве 
|
Теорема 3. Множество оптимальных планов задачи линейного программирования выпукло (если оно не пусто).
Доказательство
Если решение задачи линейного программирования единственно, то оно выпукло по определению точка считается выпуклым множеством Пусть теперь  и
и  два оптимальных плана задачи линейного программирования.
два оптимальных плана задачи линейного программирования.
Тогда 
| и 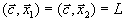 . .
|
Рассмотрим  . .
| В силу выпуклости области |
допустимых значений,  . .
| Но для этого плана |


т.е.  есть также оптимальный план и, в силу этого, множество оптимальный планов выпукло. Теорема доказана.
есть также оптимальный план и, в силу этого, множество оптимальный планов выпукло. Теорема доказана.
Теорема 4. Для того, чтобы задача линейного программирования имела решение, необходимо и достаточно, чтобы целевая функция на допустимом множестве была ограничена сверху (при решении задачи на максимум) или снизу (при решении задачи на минимум).
Эту теорему мы даем без доказательства.
Вопрос 9:
|
из
5.00
|
Обсуждение в статье: Свойства выпуклых множеств |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

