Индуктивность и емкость в цепи переменного тока

Для более глубокого понимания процессов, происходящих в последовательной RLC-цепи, целесообразно рассмотреть последовательные RL- и RC-цепи.

Для последовательной RL-цепи (рисунок 6), выражения (2) и (3) имеют следующий вид:

Модуль полного сопротивления RL-цепи при указанных на рисунке 6 параметрах компонентов на частоте

равен

Амплитуда и фаза тока:

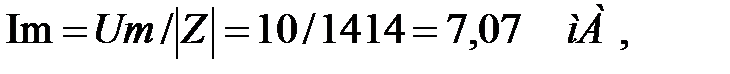
Падения напряжения на сопротивлении и индуктивности

что совпадает с показаниями приборов на рисунке 6.

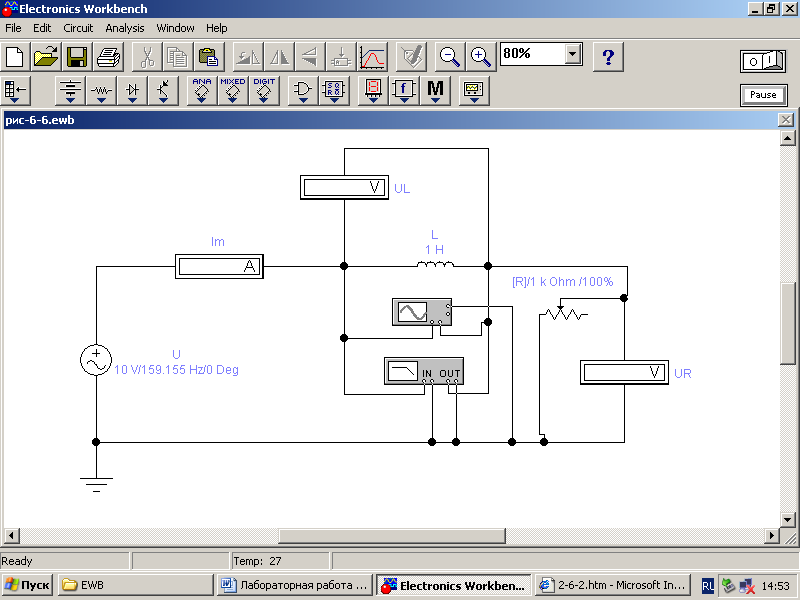
Рисунок 6 – Схема последовательной RL-цепи

 

Для определения фазовых соотношений рассмотрим осциллограммы на рисунке 7, откуда видно, что напряжение на входе RL-цепи (осциллограмма А, визирная линия 1) опережает напряжение на сопротивлении R (осциллограмма В, визирная линия 2) и, соответственно, ток в цепи на время Т2-Т1=0,000785 с. Поскольку период колебаний в данном случае равен 1/159,155=0,0063 с, то в градусах этот временной промежуток составит (360°-0,000785)/0,0063=44,98°, т.е. погрешность моделирования менее 0,05%. Заметим, что с повышением частоты этот угол стремится к 90°, что удобно наблюдать с помощью измерителя АЧХ-ФЧХ в режиме PHASE (режим ФЧХ). Результаты измерений показаны на рисунке 8, откуда видно, что уже на частоте 12 кГц (в этой точке стоит визирная линия) ток в RL-цепи запаздывает относительно напряжения на ее входе более, чем на 89°.

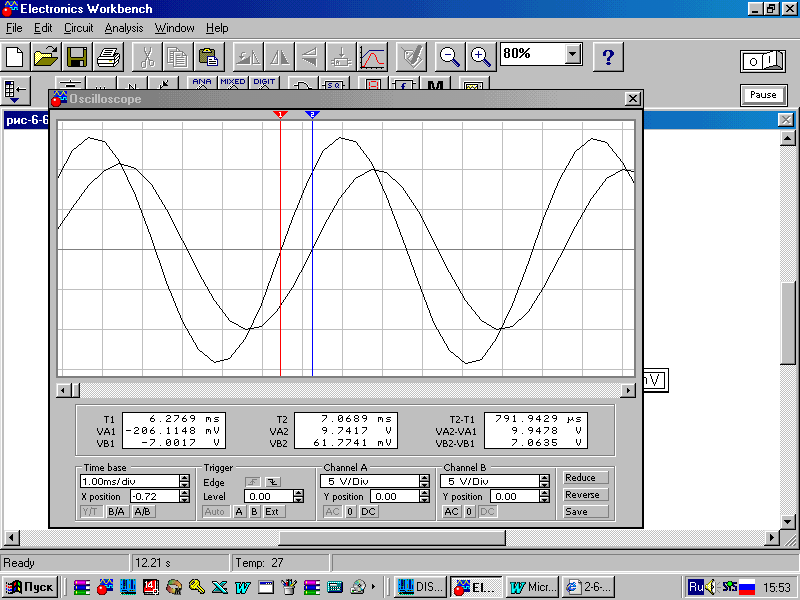
Рисунок 7 – Осциллограммы сигналов в последовательной RL –цепи

 

Рисунок 8 – Фазо-частотная характеристика последовательной RL –цепи

 

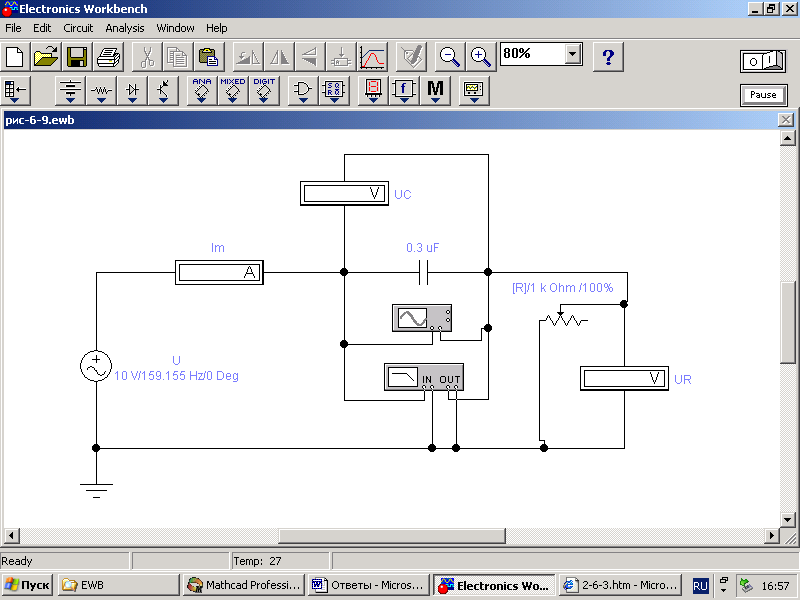
Рисунок 9 – Схема последовательной RС-цепи

Для последовательной RC-цепи (рисунок 9) из выражений (2) и (3) получаем:

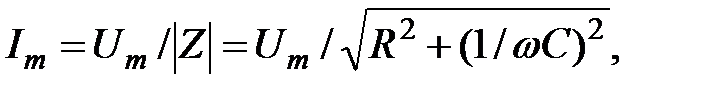
Контрольные вопросы и задания

1. Проведите расчет модуля и фазы тока в RC-цепи на рисунке 9 и сравните полученные данные с результатами моделирования, приведенными на рисунке 9. Обратите внимание на то, что в последовательной RC-цепи ток опережает входное напряжение в предельном случае на 90°. Следовательно, напряжения на емкости и индуктивности в RLC-цепи на рисунке 5 могут быть сдвинуты по фазе на 180°, чем и объясняется тот факт, что индуктивное и емкостное сопротивления входят в формулу (2) с разными знаками.

2. Почему при расчетах фазовый угол В имеет положительное значение для индуктивности и отрицательное для емкости, в то время как при моделировании результаты получаются противоположными? При поиске ответа рекомендуем обратить внимание на общее выражение для формул (2) и (3).

3. Проведите расчеты модуля и фазы тока в схемах на рисунах 6 и 9 при частоте входного сигнала 100 Гц. Результаты расчета сравните с результатами моделирования.

Практическая работа 4

Резонансные цепи

Явление, при котором индуктивное и емкостное сопротивления в RLC-цепи равны, называется резонансом.

Различают последовательный (для последовательной RLC-цепи) и параллельный (для параллельной RLC-цепи) резонанс. Последовательную RLC-цепь чаще всего называют последовательным колебательным контуром, а параллельную RLC-цепь — параллельным колебательным контуром. В случае малых потерь (сопротивление R пренебрежимо мало) для обоих контуров резонанс наступает при условии:

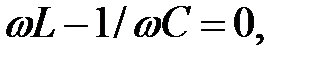
откуда получается широко известное выражение для резонансной частоты:

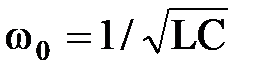или (4)

При последовательном резонансе (для последовательного контура) ток в цепи на рисунке 5 определяется только сопротивлением R и совпадает по фазе с напряжением входного сигнала. При этом ток в цепи равен I_m=U_m/R, и напряжения на индуктивности и конденсаторе:

(5)

могут превышать напряжение входного сигнала в Q раз. Безразмерная величина

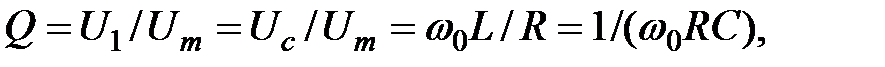(6)

называемая добротностью, показывает, во сколько раз напряжение на индуктивности или емкости при резонансе превышает входное напряжение контура. На практике используется также величина, обратная добротности, которая называется коэффициентом затухания d=l/Q. Из (6) видно, что добротность контура возрастает с увеличением индуктивности L и уменьшением сопротивления потерь R и емкости С контура.

С учетом (4) выражение (6) может быть записано также в виде:

Q=W/R,

где

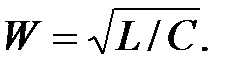(7)

Параметр W имеет размерность сопротивления и называется характеристическим сопротивлением контура.

Амплитудно-частотная характеристика резонансной цепи определяется как отношение тока, определяемого выражением (2), к току при резонансе, т.е.

(8)

В радиотехнике зависимость, описываемую выражением (8), обычно называют резонансной кривой и для малых отклонений частоты относительно резонансной частоты используют для нее приближенное выражение:

(9)

где -расстройка по частоте.

Приведем пример расчета последовательной RLC-цепи (рисунок 10). Согласно (4) при указанных на схеме значениях индуктивности и емкости:

=159,155 Гц,

что соответствует частоте входного сигнала, т.е. в цепи имеет место резонанс токов.

Значение тока в цепи I_m=U_m/R= 1/1000=1 мА соответствует показаниям амперметра I_m.

Осциллограммы сигналов в последовательном колебательном контуре показаны на рисунке 11, а, из которого видно, что напряжение на сопротивлении (осциллограмма А) и, соответственно, ток в цепи совпадает по фазе с входным напряжением (осциллограмма В).

 

 

Рисунок 10 – Последовательный резонансный контур

 

Это означает, что на резонансной частоте фазо-частотная характеристика контура (рисунок 11, б) должна иметь нулевое значение. Однако из-за дискретности визирная линия могла быть установлена на ФЧХ только вблизи резонансной частоты (»161 Гц), поэтому значение фазы составляет »3,4°.

Рисунок 11 – Осциллограмма сигналов в последовательном контуре (а) и его ФЧХ (б)

Рассмотрим резонанс токов в параллельной RLC-цепи. Наибольшее внимание резонансу этого типа уделяется в радиотехнике, где параллельный колебательный контур является основным элементом большинства частотно-избирательных устройств. В теоретических основах радиотехники показывается, что характеристики параллельного колебательного контура можно рассчитывать по формулам для последовательного контура. Однако имеются отличия, которые будут отмечены при рассмотрении конкретной схемы параллельного контура (рис. 2.12).

Рисунок 12 – Параллельный колебательный контур

 

Собственно колебательный контур состоит из двух параллельно включенных ветвей: индуктивной с сопротивлением потерь в виде внутреннего сопротивления Rl амперметра Il, и емкостной с сопротивлением потерь в виде внутреннего сопротивления Rc амперметра Iс. Напомним, что эти сопротивления могут изменяться и для рассматриваемой схемы установлены равными 1 Ом для обоих амперметров. К контуру подключены измерительные приборы, назначение которых очевидно; например, вольтметры U_l и U_r, предназначены для измерения падения напряжения на индуктивности L и на резисторе R.

Для параллельного колебательного контура вводится параметр, который равен сопротивлению контура на резонансной частоте и называется резонансным сопротивлением Rp, определяемым по формуле:

(10)

где R=R_l+R_c — суммарное сопротивление потерь контура.

Соотношение между подводимым к контуру током I_m и током в контуре Il, на резонансной частоте определяется выражением:

(11)

где Q определяется выражением (6).

В случае пренебрежения сопротивлением R выражение (11) совпадает с (4). Из (11) видно, что с увеличением потерь контура R его резонансная частота уменьшается.

Амплитудно-частотная характеристика параллельного контура рассчитывается с помощью выражения (8).

Фазо-частотная характеристика параллельного колебательного контура рассчитывается с помощью выражения (3).

Поскольку для практических применений наибольший интерес представляет область частот вблизи резонансной (в полосе , где f — текущее значение частоты), то для удобства интерпретации полученных результатов целесообразно использовать приближенную формулу для ФЧХ в виде

(12)

Из (12) видно, что при f=f₀ фазовый угол равен нулю, однако уже при незначительном отклонении частоты в одну или другую сторону от резонансной будет наблюдаться резкое изменение фазы как в область отрицательных (при f<f₀) так и положительных значений (при f>f₀). Причем, крутизна переходного участка тем больше, чем больше добротность контура, а его ширина определяется отношением f₀/Q, определяющем полосу пропускания 2Dа на уровне 0,707 (это значение получается после подстановки в выражение (2.9) значения .

Контрольные вопросы и задания

1. Дайте определения явления резонанса в электрических цепях переменного тока и назовите условия его возникновения. В каких областях техники резонансные явления находят наибольшее применение?

2. Для схемы на рисунке 12 проведите расчеты и моделирование при сопротивлениях потерь Rl=Rc=8 Ом. Уточните значение резонансной частоты с помощью соотношения (11).

3. Используя формулы (8), (3) и значения параметров на рисунке 12, рассчитайте амплитудно-частотную и фазо-частотную характеристики и сравните полученные результаты с данными моделирования.