 |
Главная |
Расчёт балки на упругом основании
|
из
5.00
|
Для двутавровой балки, расположенной на упругом основании, при модуле упругости равном E= 210 ГПа требуется:
1.Записать с помощью метода начальных параметров выражения для прогибов v, углов поворота поперечных сечений и, изгибающих моментов Mи поперечных сил Qна всех участках балки.
2.Поставить граничные условия и определить неизвестные начальные параметры.
3.Провести расчеты на компьютере и построить эпюры Q, M,  , v.
, v.
4.Построить эпюру реактивного отпора основания.
5.Определить реакции опор, если они имеются.
6.Проверить прочность балки, приняв коэффициент надежности по нагрузке  , расчетное сопротивление R= 210 МПа и коэффициент условий работы
, расчетное сопротивление R= 210 МПа и коэффициент условий работы 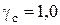 .
.
Исходные данные
| Шифр | Двутавр № | l м | F кН | М кНм | q кН/м | k0 Н/cм3 |
| 31-6 | 6,0 |
Расчётная схемаАналитическое решение
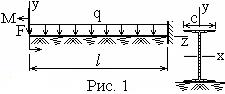 Для балки в виде стального прокатного двутавра №22 выпишем осевой момент инерции J = Jx = 2550 см4 и ширину полки с = 11 см. Обозначим и определим жёсткость балки
Для балки в виде стального прокатного двутавра №22 выпишем осевой момент инерции J = Jx = 2550 см4 и ширину полки с = 11 см. Обозначим и определим жёсткость балки
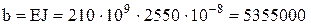 Нм
Нм  .
.
Для упрощения дальнейших вычислений введём обозначения безразмерной переменной 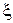 , коэффициента постели k и затем вычислим параметр
, коэффициента постели k и затем вычислим параметр 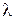
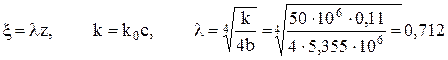 1/м.
1/м.
Запишем с помощью метода начальных параметров выражение для прогиба балки в произвольном сечении
 (1)
(1)
Здесь v0,  - начальные параметры, представляющие собой прогиб и угол поворота в начале координат, т. е. на левом конце балки z = 0
- начальные параметры, представляющие собой прогиб и угол поворота в начале координат, т. е. на левом конце балки z = 0 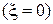 . Y1, Y2, Y3, Y4 – функции А.Н.Крылова, которые определяются из специальных таблиц или по формулам:
. Y1, Y2, Y3, Y4 – функции А.Н.Крылова, которые определяются из специальных таблиц или по формулам:
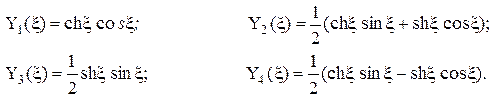 (2)
(2)
Эти функции обладают свойством повторяемости при дифференцировании
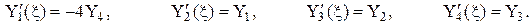 (3)
(3)
Пользуясь формулой (1) и далее вытекающими из неё выражениями для характеристик балки, следует помнить, что нагрузки M, F, q имеют знаки, установленные для них в методе начальных параметров и зависящие от их направлений. В частности, в данной задаче эти знаки будут отрицательными.
Неизвестные начальные параметры определим из граничных условий на правом конце балки:
 (4)
(4)
Смысл уравнений (4) в том, что прогиб и угол поворота правого концевого сечения должны равняться нулю вследствие его заделки.
Запишем выражения для углов поворота поперечных сечений, изгибающих моментов и поперечных сил.
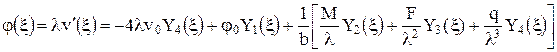 . (5)
. (5)
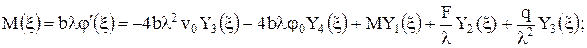 (6)
(6)
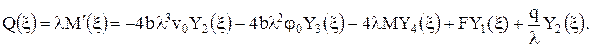 (7)
(7)
Вычисляем аргументы и значения функций А.Н.Крылова для выполнения граничных условий (4)
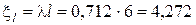 ,
, 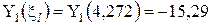 ,
,
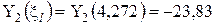 ,
,  ,
, 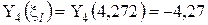 .
.
Раскроем граничные условия (4) с помощью формул (1) - (3). При этом единицы измерения силовых величин для удобства вычислений переведём в килоньютоны.

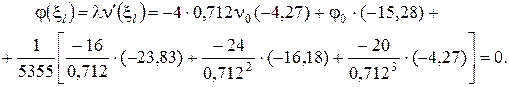
После элементарных упрощений получена система двух алгебраических уравнений относительно 
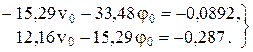
Решая, имеем
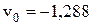 см,
см, 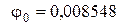 рад.
рад.
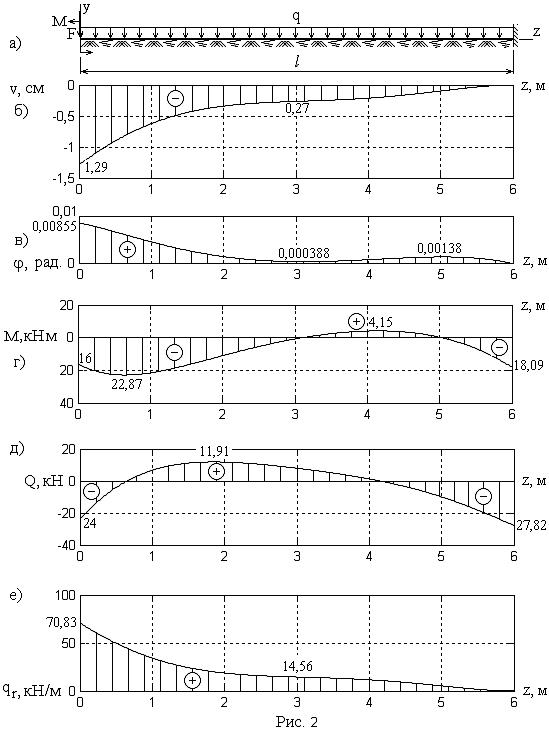 |
Далее расчёты производим с помощью компьютерной программы кафедры теоретической и прикладной механики. Полученные эпюры
 приведены на рис. 2. Числа, подписанные для характерных точек, взяты визуально с экрана монитора при многократных увеличениях графиков и обладают высокой степенью точности.
приведены на рис. 2. Числа, подписанные для характерных точек, взяты визуально с экрана монитора при многократных увеличениях графиков и обладают высокой степенью точности.
Реакции в правой опоре можно определить по эпюрам изгибающих моментов 2в и поперечных сил 2г или по обращению к компьютеру с запросом. Получено, что они имеют значения
Ml =18,09 кНм, направлен по часовой стрелке,
Rl = 27,82 кН, направлена вверх.
Ординаты реактивного отпора основания определяем по формуле Винклера
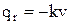 .
.
Здесь знак минус учитывает, что  имеют противоположные направления. Результаты счёта на компьютере показаны на рис. 2е. Равнодействующая этой реакции, вычисленная как определённый интеграл методом трапеций, составляет
имеют противоположные направления. Результаты счёта на компьютере показаны на рис. 2е. Равнодействующая этой реакции, вычисленная как определённый интеграл методом трапеций, составляет
R = 116,79 кН.
Проверим равновесие балки.
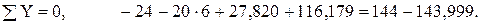
Относительная погрешность составляет
 .
.
Очевидно, что равновесие обеспечено. Вычисления правильны.
Расчётное значение наибольшего изгибающего момента равно:
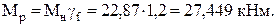
Выполняем проверку условия прочности
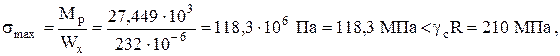
где 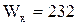 см
см  - момент сопротивления двутавра №22.
- момент сопротивления двутавра №22.
Условие прочности выполняется. Прочность обеспечена.
Решение методом конечных разностей
Изогнутая ось балки описывается обыкновенным дифференциальным уравнением четвёртого порядка
 , (8)
, (8)
k – коэффициент постели, знак минус в правой части соответствует нагрузке, направленной вниз. Разделим уравнение на 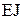 , обозначим
, обозначим
 .
.
и получим вместо (8)
 . (9)
. (9)
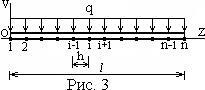 Область непрерывного изменения аргумента
Область непрерывного изменения аргумента  заменим областью дискретного изменения аргумента –сеткой (рис. 3)
заменим областью дискретного изменения аргумента –сеткой (рис. 3)
 .
.
Множество точек с номерами 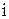 называется сеткой, а сами точки - узлами сетки. Вместо функции непрерывного аргумента
называется сеткой, а сами точки - узлами сетки. Вместо функции непрерывного аргумента 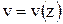 будет отыскиваться сеточная функция
будет отыскиваться сеточная функция 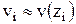 .
.
К уравнению (6) присоединяются граничные условия. На левом конце балки изгибающий момент и поперечная сила в сечении равны приложенным нагрузкам
 . (10)
. (10)
На правом конце балки - заделка. Поэтому прогиб и угол поворота сечения равны нулю
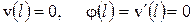 . (11)
. (11)
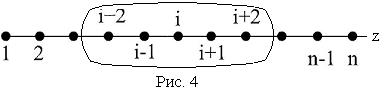 |
Пользуясь пятиточечным шаблоном сетки (рис. 4),
заменим производные в задаче (6) – (8) конечноразностными соотношениями:
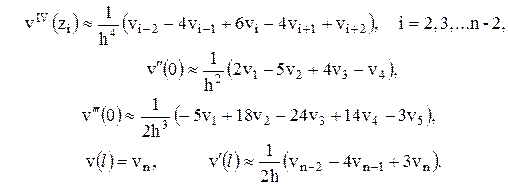 (12)
(12)
Подстановка (12) в задачу (9) – (11) и несложные преобразования приводят к системе алгебраических уравнений относительно вектора 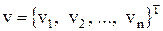
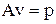 , (13)
, (13)
где
A = 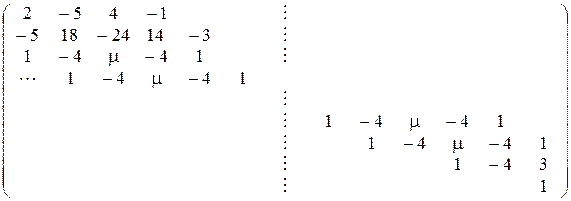 ,
,
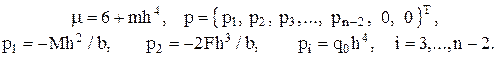
Нулевые элементы матрицы не показаны, значок 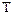 в индексе соответствует операции транспонирования.
в индексе соответствует операции транспонирования.
Система уравнений (13) решается на компьютере с помощью подпрограммы пакета математических программ MATLAB, в результате чего становится известным вектор v.
Далее с помощью конечноразностных замен производных вычисляются угол поворота и внутренние силы в сечениях по формулам
 .
.
Реактивный отпор основания определяем, как и в предыдущем варианте решения, с помощью формулы Винклера
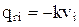 .
.
Результаты счёта, выданные в виде графиков на экран компьютера, почти точно совпадают с данными эпюр, изображённых на рис. 2.
|
из
5.00
|
Обсуждение в статье: Расчёт балки на упругом основании |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

