 |
Главная |
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ. СТАТИСТИЧЕСКИЙ ХАРАКТЕР РАДИОАКТИВНОГО РАСПАДА
|
из
5.00
|
РАБОТА № 5
СТАТИСТИЧЕСКИЙ ХАРАКТЕР РАДИОАКТИВНОГО РАСПАДА
Цель работы: ознакомиться со статистическими закономерностями процесса радиоактивного распада, определить характеристики распределения Пуассона для конкретного случая.
Приборы и принадлежности: бета активный препарат, пересчетный прибор, компьютер.
ВВЕДЕНИЕ
Измерение макроскопических величин (например, массы какого-либо тела, длины стержня и т.д.) производится с той или иной степенью точности. Это обусловлено как точностью прибора, так и особенностями самого процесса измерения. Поэтому можно сказать, что сама по себе измеряемая величина (масса, длина стержня и т.д.) имеет некоторое волне определенное значение, в то время как результаты измерений флуктуируют из-за несовершенства измерительных приборов, недостаточной их изоляции от внешних условий и т.д. Совсем иначе обстоит дело со многими измерениями в ядерной физике. В отличие от макромира флуктуации измеряемых величин связаны, как правило, с самой сутью явлений и поэтому не могут быть сделаны сколь угодно малыми. Так, если речь идет об измерении числа актов радиоактивного распада, происшедших за какое-то время, то флуктуирует сама измеряемая величина, а измерительный прибор (счетчик частиц) в первом приближении можно считать идеальным, то есть не подверженным статистическому влиянию окружающих условий.
Роль статистического подхода к явлениям микромира значительно глубже, чем в макромире. Статистика здесь нужна не только для обработки результатов измерений, но и для изучения самой природы исследуемых явлений. Например, природа радиоактивности была окончательно установлена только после завершения подробного статистического анализа, показавшего, что различные акты распада между собой статистически независимы. Последнее означает, что момент распада определенного ядра радиоактивного изотопа не зависит ни от предыстории источника излучения, ни от состояния атомов, находящихся в окрестностях рассматриваемого атома.
Поскольку каждый акт распада является случайным событием, то в течение определенного интервала времени t распадается различное число ядер. Если обозначить через Ni число распадов, зарегистрированных за время t в i-том измерении, то не все Ni будут одинаковыми. Однако большинство этих величин будет близко к среднему значению áNñ:
áNñ = (N1 + N2 + ... + Nk) / k
(здесь k - число измерений).
Чем больше отличие Ni от áNñ, тем меньше Р(Ni)- вероятность обнаружить это значение Ni:
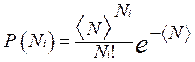 (1).
(1).
Формула (1) называется распределением Пуассона. Из (1) можно найти среднеквадратичное отклонение[1] DN числа зарегистрированных распадов от áNñ:
DN=  (2)
(2)
и относительное отклонение dN:
 (3).
(3).
Если áNñ велико (áNñ>>1), то различные значения Ni можно считать распределенными непрерывно. В этом случае распределение Пуассона переходит в распределение Гаусса:
 (4),
(4),
где  (5)
(5)
- функция распределения Гаусса,  - среднеквадратичное отклонение N от <N>. Произведение F(N)×dN = dW(N) есть вероятность того, что значение измеренной величины N лежит в пределах от N до N + dN. Вывод соотношений (1) – (5) дан в Приложении к работе.
- среднеквадратичное отклонение N от <N>. Произведение F(N)×dN = dW(N) есть вероятность того, что значение измеренной величины N лежит в пределах от N до N + dN. Вывод соотношений (1) – (5) дан в Приложении к работе.
В настоящей работе изучается статистика бета распада и проверяется распределение Гаусса (4). Для этого необходимо провести достаточно большое число наблюдений актов распада, происходящих в течение определенного времени, и вычислить вероятность того или иного значения числа распадов, а затем сравнить ее с вероятностью, даваемой соотношением (4).
МЕТОДИКА ИЗМЕРЕНИЙ
В работе регистрируется поток бета частиц, возникающих при распаде радиоактивного препарата. Мощность источника в этой работе достаточно мала, поэтому работа с ним не требует специальных мер безопасности.
Интенсивность потока бета частиц определяют с помощью газоразрядного счетчика. Число частиц, зарегистрированных счетчиком, за некоторый промежуток времени пропорционально числу распадов, происшедших за это время. Из-за случайности процесса распада число регистрируемых счётчиком частиц будет различным в различных измерениях, однако в этом случайном процессе есть своя закономерность, в силу которой число регистрируемых частиц подчиняется закону распределения Гаусса (4). Для проверки этого закона вам необходимо произвести достаточно длительный ряд измерений числа бета частиц, зарегистрированных счётчиком за равные промежутки времени.
Для этого, во-первых, необходимо подобрать положение источника бета излучения относительно детектора таким образом, чтобы за время измерения 10 секунд счетчик регистрировал около 500 импульсов. Во-вторых, необходимо произвести 200 измерений импульсов от счетчика. Каждое измерение проводится в течение 10 секунд. Импульсы от счетчика поступают в пересчетную схему, работа которой управляется с помощью реле времени, и одновременно эти же импульсы подаются в последовательный порт компьютера.
Компьютер, получая сигналы от счётчика, подсчитывает число этих сигналов в течение определённых промежутков времени, например каждые 10 секунд, и строит на экране гистограмму числа этих сигналов.
Гистограмма строится следующим образом. По оси абсцисс откладывается число импульсов Ni , зарегистрированных в отдельных измерениях (i – номер измерения), причем в качестве интервала изменения Ni принимают величину DN ~ 10 ¸ 20, т.е. на оси абсцисс откладывают значения 400, 410, ... 500, 510, ... ( DN = 10) или, 400, 420, ..... 500, 520 .... (DN = 20).
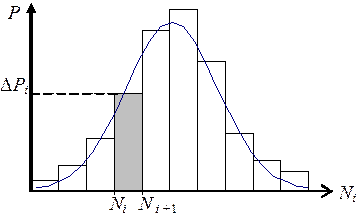 Рис. 1
Рис. 1
|
На каждом интервале DN, как на основании, строится прямоугольник, высота которого равна числу измерений DРi, в которых зарегистрировано число импульсов, заключенных в пределах от Ni до Ni+1 =Ni + DN (см. Рис. 1).
Очевидно, сумма всех DРi равна полному числу N измерений, проделанных к данному моменту времени (в нашем случае число N не превышает максимального значения Nmax = 200). Примерный вид гистограммы изображен на рис. 1.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Включите питание счётчика и АЦП. Подберите положение источника бета излучения относительно детектора таким образом, чтобы за время измерения 10 секунд счетчик регистрировал около 500 импульсов. За помощью в этих манипуляциях обратитесь к лаборанту.
2. Включите компьютер и запустите программу Счётчик, щёлкнув мышью на её иконке  , расположенной на рабочем столе Windows. В результате откроется окно, изображённое на Рис. 2.
, расположенной на рабочем столе Windows. В результате откроется окно, изображённое на Рис. 2.
Щёлкните на пункте меню Канал и выберите в раскрывшемся меню пункт Новый (см. Рис. 2). Раскроется новое окно (Рис. 3), в котором необходимо будет ввести параметры эксперимента.

Рис. 2

Рис. 3
Вверху окна необходимо выбрать один из двух измерительных каналов, щёлкнув на одном из переключателей Канал 1 или Канал 2. Суть этого выбора в том, что в данной работе один компьютер может обслуживать два счётчика, и вам необходимо указать какой именно из счётчиков вы будете использовать для измерений. Выбор счётчика определяется его расположением на столе по отношению к компьютеру: счётчик слева от компьютера – Канал 1, справа – Канал 2.
Кроме того, справа вверху окна необходимо выбрать тип измерений, щёлкнув на одном из переключателей Одиночные или Непрерывные. В данной работе необходимо выбрать Непрерывные измерения. В этом случае в процессе измерений вы получите на экране гистограмму. Случай Одиночные относится к работе № 6.
Далее впишите вашу фамилию в соответствующее окошко. Оставлять его пустым нельзя, иначе вы не сможете перейти к дальнейшим действиям, окно просто не закроется.
3. В окошках со стрелками справа задайте параметры эксперимента:
Длительность отсчёта рекомендуется задать 10 секунд, хотя возможны и другие значения.
Число измерений рекомендуется задать равным 200, хотя также можно указать и другое значение.
Число столбцов гистограммы также может быть любым, однако, чем это число больше, тем сильнее будет проявляться случайность процесса распада и высота столбцов может сильно флуктуировать, т.е. заметно отличаться от той высоты, что даётся законом распределения Гаусса (4). Одним словом, задавать число столбцов большим 15 ¸ 20 не следует; оптимальным значением числа столбцов можно считать 10 при 500 импульсах счётчика за 10 секунд измерений.
По окончании ввода нажмите кнопку Ok. Окно ввода параметров закроется и раскроется основное окно программы (Рис. 4).
Рис. 4
В рабочем окне в левой верхней его части выводятся установленные вами параметры эксперимента. Изменять их уже нельзя, эти параметры выводятся лишь для контроля. Если вы увидели, что заданные параметры неверны, то придётся закрыть это окно, нажав на кнопку Выход, а затем повторить вновь всю описанную выше процедуру установки параметров эксперимента. Нажав в рабочем окне кнопку Старт, вы запускаете процесс измерений.
Если необходимо подключить также и другой измерительный канал, то процедура установления параметров эксперимента для него та же самая, при этом не нужно останавливать измерения в уже открытом канале. Точно так же вызываете пункт меню Канал, в нём нажимаете Новый, задаёте параметры эксперимента и нажимаете кнопку Ok. К уже открытому окну одного канала добавится окно другого канала. Нажимаете в нём кнопку Старт и запускаете процесс измерений (Рис. 5).

Рис. 5.
Если при ваших манипуляциях с окнами каналов они изменили своё месторасположение, наехали одно на другое и т.п., то выровнять их проще всего с помощью опции меню Окно. Вызвав её вы откроете меню из одного пункта Выровнять. Щёлкнув на нём, вы восстановите прежний вид и расположение окон.
4. Для начала измерений нажмите кнопку Старт. В нижней части окна начнёт строиться гистограмма. Её вид будет периодически обновляться после завершения подсчёта числа импульсов, в течение очередного установленного вами интервала измерений (например, каждые 10 секунд).
5. Если вам по какой – либо причине нужно прервать на некоторое время эксперимент, то для этого нажмите кнопку Пауза. Процесс измерений остановится, а на кнопке появится надпись Продолжить. Вновь нажав на эту кнопку вы продолжите измерения, а надпись на кнопке станет прежней: Пауза.
6. По окончании измерений в верхнем окошке справа (окно Номер измерения) появится число равное заданному вами Числу измерений и кнопка Печать станет активной. Теперь распечатайте результаты ваших измерений. Для этого нажмите кнопку Печать, после чего откроется обычный диалог печати Windows. Там вы можете задать необходимые установки печати и вызвать процесс печати. Принтер распечатает рабочее окно с гистограммой и всеми установками эксперимента. Если печать в данный момент невозможна по какой-либо причине, то вы сможете выполнить её позже на другом компьютере, поскольку результаты сохраняются в файле Channel_1.bmpилиChannel_2.bmp, в зависимости от того, в каком канале вы производили измерения. Файлы находятся здесь же на рабочем столе Windows, где и ярлык программы. Вы можете скопировать их на любой носитель и затем распечатать на другом компьютере. Однако следует иметь в виду, что результаты вашей работы сохранятся в этих файлах только по окончании процесса измерений.
7. По результатам измерений (гистограмме) рассчитайте среднее значение áNñ числа зарегистрированных импульсов и дисперсию s:

где  , k - число прямоугольников гистограммы.
, k - число прямоугольников гистограммы.
8. Убедитесь, что вычисленные s и  имеют близкие значения.
имеют близкие значения.
9. Сравните построенную гистограмму с кривой распределения Гаусса F(N). Для этого по формуле (5) вычислите значения F(N) при N , принимающем различные значения  , а в качестве s возьмите
, а в качестве s возьмите  . Затем, на том же графике, на котором построена гистограмма, отложите вычисленные значения
. Затем, на том же графике, на котором построена гистограмма, отложите вычисленные значения  и, соединив их плавной кривой, получите кривую распределения Гаусса (см. кривую на рис. 1).
и, соединив их плавной кривой, получите кривую распределения Гаусса (см. кривую на рис. 1).
10. Покажите, что ~ 68% результатов отличаются от áNñ не более чем на  . Для этого необходимо найти отношение числа измерений, в которых получилось число импульсов в интервале от
. Для этого необходимо найти отношение числа измерений, в которых получилось число импульсов в интервале от  до
до  к полному числу измерений (в нашем случае - 200).
к полному числу измерений (в нашем случае - 200).
11. Методом c2 проверьте совпадение гистограммы с распределением Гаусса. (О методе c2 см. Приложение к работе.)
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Согласно закону радиоактивного распада среднее число ядер N, не распавшихся за время t, связано с начальным числом ядер N0 соотношением:
N=N0 ×e–lt,
где l - постоянная распада. Какой физический смысл имеет N, если N0 = 1?
2. Акт распада является случайным событием. Поэтому число атомов, не распавшихся за время t, есть случайная величина. В законе же радиоактивного распада величина N отнюдь не случайная. Почему?
3. Сформулируйте центральную предельную теорему теории вероятностей.
4. Какая связь между полученной вами гистограммой и законом радиоактивного распада?
[1] Напомним, что по определению
|
из
5.00
|
Обсуждение в статье: ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ. СТАТИСТИЧЕСКИЙ ХАРАКТЕР РАДИОАКТИВНОГО РАСПАДА |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

