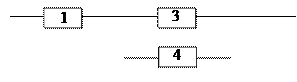|
Главная |
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА
|
из
5.00
|
ЗАДАНИЕ 1
| Вариант 1. Брошено три монеты. Найти вероятности событий: А- выпадение герба на первой монете, В - выпадение ровно двух гербов. Зависимы ли события А и В ? |
| Вариант 2. В первой урне 2 белых и 3 черных шара. Во второй урне 3 белых. Из каждой удалили по одному, наугад взятому шару, а оставшиеся шары поместили в третью урну (пустую). Какова вероятность события А - шар наугад взятый из 3-й урны белый? |
| Вариант 3. Из 20 лотерейных билетов 4 выигрышных. Три человека по очереди будут по одному билету. Найти вероятности событий: А1 - первый возьмет выигрышный, А2 - второй возьмет выигрышный. |
| Вариант 4. В первой урне 1 белый и 4 черных шара, во второй - 1 белый и 2 черных. В первую урну добавили один шар, наугад взятый из второй урны. После этого из 1-й урны наугад извлекли 1 шар. Какова вероятность того, что этот шар белый: |
| Вариант 5. Игральная кость брошена 2 раза. Х1 - количество очков при первом бросании, Х2 - количество очков при втором бросании. События: А={Х1 делится на 2}, В={Х2 делится на 2}. Найти вероятность произведения АВ. Зависимы ли события А и В? |
| Вариант 6. Из урны, содержащей 2 белых и 2 черных шара, извлекают по одному без возвращения все шары. Найти вероятности событий: 1) третий шар белый, 2) третий и четвертый шары белые, 3) четвертый - белый, при условии, что третий был белым. |
| Вариант 7. В первой урне 1 белый и 2 черных шара, во второй - 2 белых и 3 черных. Из первой и второй урн взяли наугад по одному шару и поместили в третью (пустую) урну. Какова вероятность того, что взятый наугад из 3-й урны шар окажется белым? |
| Вариант 8. Игральная кость брошена два раза. Х1 - количество очков при первом бросании, Х2- количество очков при втором бросании. События: А={Х1 делится на 2} В={Х2 делится на 3}. Найти вероятности: Р(А), Р(В), Р(АВ). Зависимы ли события А и В? |
| Вариант 9. Из пяти карточек с номерами 1,2,3,4,5 наугад извлекают одну, регистрируют ее номер Х, а карточку возвращают в общую совокупность. После этого вторично извлекают наугад карточку и регистрируют ее номер Y. Какова вероятность того, что хотя бы одно из чисел: Х, Y равно 3, если Х+Y - четное число? |
| Вариант 10. Брошены две игральные кости. События: А={число очков на 1-й кости делится на 2} В={ сумма очков, выпавших на 1-й и 2-й костях, делится на 4} Зависимы ли события А и В? Найти вероятности: Р(А), Р(В), Р(АВ), Р(В/А), Р(А/В). |
| Вариант 11. Из ящика, содержащего три билета с номерами 1,2,3, извлекают по одному все билеты. Предполагая, что все последовательности номеров билетов имеют одинаковые вероятности, найти вероятность того, что хотя бы у одного билета порядковый номер совпадет с его собственным номером. |
| Вариант 12. Имеется 5 урн с шарами. В 1-й, 2-й и 3-й содержатся по 2 белых и по одному черному, а в 4-й и 5-й - по одному белому и одному черному. Наугад выбирается одна урна и из нее берут наугад один шар. Какова вероятность того, что этот шар белый? |
| Вариант 13. Игральная кость брошена 2 раза. Х1 и Х2 - количество очков, выпавших при первом и втором бросании. События: А={Х1 делится на 2, Х2 делится на 4}; В={Х1 делится на 3}. Зависимы ли события А и В? |
| Вариант 14. В первой урне находилось 2 белых и 3 черных шара, во второй урне - 3 белых и 2 черных. Из первой урны во вторую переложили один шар. После этого извлекли наугад один шар из второй урны. Какова вероятность того, что этот шар белый? |
| Вариант 15. Игральная кость брошена 2 раза. Пусть Х1 и Х2 - количества очков, выпавших на верхних гранях. Рассмотрим события: А={6£Х1 + Х2 £ 8}, В={Х1 - четное число}. Зависимы ли события А и В? |
| Вариант 16. В первой урне содержатся 4 белых и 2 черных шара, во второй - 2 белых и 4 черных. Из второй урны переложили в первую урну один шар, а затем взяли из 1-й урны наугад 1 шар. Какова вероятность того, что этот шар черный? |
| Вариант 17. Игральная кость брошена 2 раза. Х1 и Х2 - количества очков, выпавших на верхних гранях. События: А={-2£Х1 - Х2 £2}, В={Х1 = Х2} . Зависимы ли события А и В? Найти вероятности: Р(А), Р(В), Р(АВ), Р(В/А). |
| Вариант 18. Брошены две игральные кости. Х1 - количество очков, выпавших на 1-й кости, Х2 - количество очков, выпавших на 2-й кости. События: А={Х1 делится на 3}, В={Х1 +Х2 ³10}. Зависимы ли события А и В? Найти вероятности: Р(А), Р(В), Р(АВ), Р(А/В). |
| Вариант 19. Из урны, содержащей два белых и два черных шара, извлекли один шар наугад, а затем добавили два белых и один черный. Какова вероятность того, что извлеченные после этого два шара окажутся оба белыми? |
| Вариант 20. Из урны, содержащей два белых и один черный шар, извлекают по одному все шары. Какова вероятность того, что третий шар окажется белым? |
| Вариант 21. Из урны, содержащей 3 шара с номерами 1,2,12, извлекают наугад один шар. Ак - {на извлеченном шаре содержится цифра к} (к=1,2). Зависимы ли события А1, А2? |
| Вариант 22. Из урны, содержащей два белых и три черных шара, наугад извлекли два шара, а затем добавили один черный шар. Какова вероятность того, что извлеченный после этого наугад шар окажется белым? |
| Вариант 23. Из урны, содержащей 2 белых и 4 черных шара, удалили два наугад, а затем извлекли 3-й шар. Какова вероятность того, что этот шар белый? |
| Вариант 24. В первой урне 4 белых и 2 черных шара, во второй 2 белых и 4 черных. Из первой урны переложили во вторую один шар. После этого из второй урны извлекли один шар. Какова вероятность того, что шар, взятый из 2-й урны, черный? |
| Вариант 25. Имеются 3 урны с шарами: В 1-й и 2-й по 2 белых и 3 черных шара. В 3-й урне белых шаров столько же, сколько и черных. Найти вероятность того, что извлеченный из наугад взятой урны шар окажется белым. Шар оказался черным. Какова вероятность того, что он извлечен из 3-й урны? |
ЗАДАНИЕ 2
Вариант 1.
|
Система может работать в двух режимах: благоприятном и неблаго-приятном. Вероятности отказов элементов соответственно равны: при благоприятном режиме 0,1; 0,05; 0,2; 0,1, при неблагоприятном режиме 0,2; 0,1; 0,3; 0,2. Определить надёжность системы, если в неблагоприятном режиме система работает 20% времени.
Вариант 2.
|
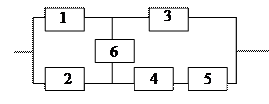
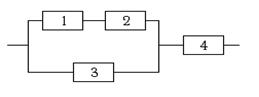
| Определить надёжность системы. Надёжности элементов соответст-венно равны 0,8; 0,9; 0,8; 0,6, 0,7; 0,9. |
Вариант 3.
|
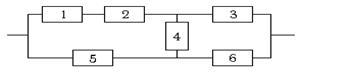
| Надёжности элементов системы соответственно равны 0,8; 0,7; 0,9. В результате эксплуатации система отказала. Найти вероятность того, что отказал только элемент с номером 3. |
Вариант 4.
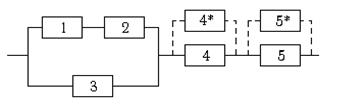
|
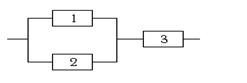
| Надёжности элементов системы соответственно равны 0,8; 0,7; 0,9; 0,6; 0,8. На сколько процентов повысится надёжность системы, если элементы 4 и 5 дублировать такими же элементами (каждый элемент дублируется отдельно). |
Вариант 5.
В системе выделены два элемента, отказы которых независимы. Вероятности отказов равны 0,1 и 0,2. Система может отказать лишь в результате отказа по меньшей мере одного из этих элементов. Вероятность отказа системы при отказе только первого элемента равна 0,5, при отказе только второго элемента – 0,6, а при отказе обоих – 0,9. Найти вероятность отказа системы.
Вариант 6.
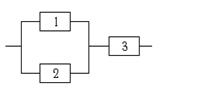
|
Система состоит из трёх взаимо-заменяемых элементов, соединённых по схеме. У сборщика имеются два элемента первого сорта с надёжностью 0,9 и один элемент второго сорта с надёжностью 0,7. Элементы монтируются наугад. В результате эксплуатации система вышла из строя. Найти вероятность того, что элемент с номером 2 оказался второго сорта.
Вариант 7.
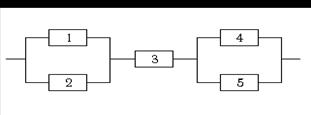
|
Надёжности элементов системы соответственно равны 0,7; 0,7; 0,9; 0,8; 0,8. В результате эксплуатации система вышла из строя из-за отказа элемента с номером 3. Вышедший из строя элемент заменяют, беря его наугад из запасных частей. При этом имеются пять аналогичных элементов первого сорта с надёжностью 0,9 и три элемента второго сорта с надёжностью 0,7. Найти надёжность системы после ремонта.
Вариант 8.
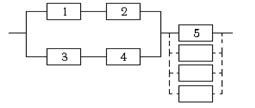
|
Надёжности элементов системы соответственно равны 0,7; 0,8; 0,6; 0,9; 0,8. Элемент 5 можно дублировать. Имеются три резервных элемента с такой же надёжностью. Сколько достаточно поставить дублирующих элементов, чтобы повысить надёжность на 20%? На сколько процентов повысится надёжность системы, если использовать для дублирования все имеющиеся резервные элементы?
Вариант 9.
|
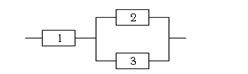
Система состоит из трёх взаимо-заменяемых элементов, соединённых по схеме. У сборщика имеются два элемента первого сорта с надёжностью 0,9 и один элемент второго сорта с надёжностью 0,7. Элементы монтируются наугад. Определить надёжность системы.
Вариант 10.
|
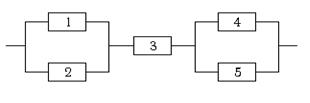
Система может работать в двух режимах: нормальном и с перегрузкой. Надёжности элементов соответственно равны: при нормальном режиме 0,8; 0,8; 0,9; 0,7; 0,7, при работе с перегрузкой 0,7; 0,7; 0,8; 0,6; 0,6. Определить надёжность системы, если с перегрузкой системе приходится работать 15% времени.
Вариант 11.
|
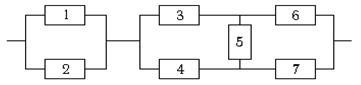
| Определить надёжность системы. Вероятности отказов элементов системы соответственно равны 0,3; 0,3; 0,2; 0,2, 0,4; 0,1; 0,1. |
Вариант 12.
|
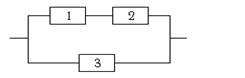
| Надёжности элементов системы соответственно равны 0,7; 0,8; 0,6. В результате эксплуатации система отказала. Найти вероятность того, что отказали только элементы с номерами 2 и 3. |
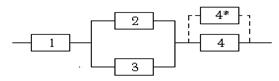
Вариант 13.
|
Надёжности элементов системы соответственно равны 0,8; 0,6; 0,6; 0,7. Для повышения надёжности к элементу с номером 4 присоединяется параллельно ещё один элемент. Какова должна быть его надёжность, чтобы надёжность всей системы повысилась на 20%?
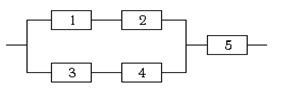
Вариант 14.
|
| Надёжности элементов системы соответственно равны 0,7; 0,8; 0,6; 0,9; 0,8. В результате эксплуатации система отказала. Найти вероятность того, что отказал только элемент с номером 5. |
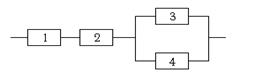
Вариант 15.
|
У сборщика имеются три элемента первого сорта с надёжностью 0,8 и один элемент второго сорта с надёжностью 0,7. Элементы монтируются наугад. Определить надёжность системы.
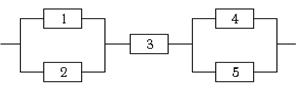
Вариант 16.
|
| Надёжности элементов системы соответственно равны 0,7; 0,7; 0,8; 0,6; 0,6. В результате эксплуатации система отказала. Найти вероятность того, что отказали только элементы с номерами 1 и 2. |
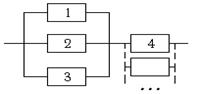
Вариант 17.
|
| Надёжности элементов системы соответственно равны 0,7; 0,7; 0,8; 0,8. Элемент с номером 4 можно дублировать. Для этого имеются три запасных элемента с такой же надёжностью. Сколько достаточно поставить дублирующих элементов, чтобы повысить надёжность системы на 20%? |
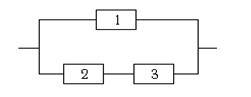
Вариант 18.
|
Система состоит из трёх взаимо-заменяемых элементов, соединённых по схеме. У сборщика имеются два элемента первого сорта с надёжностью 0,8 и один элемент второго сорта с надёжностью 0,7. Элементы монтируются наугад. Определить надёжность системы.
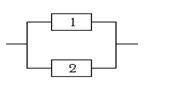
Вариант 19.
|
Система состоит из двух дублирующих друг друга элементов. У сборщика имеются восемь элементов. Из них шесть первого сорта с надёжностью 0,9 и два элемента второго сорта с надёжностью 0,8. Определить надёжность системы.
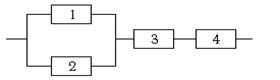
Вариант 20.
|
| Надёжности элементов системы соответственно равны 0,7; 0,7; 0,8; 0,9. В результате эксплуатации система отказала. Найти вероятность того, что отказали только элементы с номерами 1 и 2. |
Вариант 21.
|
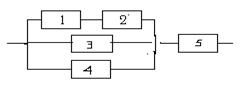
Элементы в системе соединены по схеме. Заданы надежности элементов: 0,8; 0,9; 0,6; 0,7 и 0,8. Для повышения надежности элемент 5 дублируется еще одним элементом. Какова должна быть надежность дублирующего элемента, чтобы надежность всей системы повысилась на 15%?
Вариант 22.
        
режиме 0,2; 0,3; 0,1; 0,1; 0,2, 0,4; 0,3; 0,3; 0,4. Определить благоприятном режиме она
| Элементы в системе соединены по схеме. Система может работать в 2-х режимах: благоприятном и неблагоприят-ном. Вероятности отказа элементов: при благоприятном при неблагоприятном режиме 0,5; надежность системы, если в работает 90% времени. |
Вариант 23.

|
Элементы в системе соединены по схеме. Надежности элементов: Р1=0,8; Р2=0,9; Р3=0,7. Система испытывалась в течение времени Т и проработала безотказно. Найти вероятность того, что все это время работали бы все 3 элемента.
Вариант 24.
| Определить надежность систе-мы. Надежности элементов соот-ветственно равны 0,7; 0,8; 0,9; 0,6; 0,7; 0,8. |
Вариант 25.
   
| Элементы соединены по схеме надежности элементов 0,9; 0,7; 0,7 и 0,7. В результате эксплуатации система отказала. Найти вероят-ность того, что отказал только 1-й элемент. |
ЗАДАНИЕ 3
Выписать закон распределения дискретной случайной величины Х; Найти М[x], D[x], s[x]. Построить график функции распределения F(x).
Вариант 1. Из перетасованной колоды (36 карт) снимают по одной карте до появления туза, но не более 4-х. Х - число снятых карт.
Вариант 2. Рассеянный с улицы Бассейной решил обсудить качество кваса, но забыл последнюю цифру телефона кассы, помнит лишь, что это либо 1, либо 3, либо 7, либо 8. Х - число наборов номера до верного соединения.
Вариант 3. Бывший лучший королевский стрелок после препирательства с королем стреляет в Чудо-Юду из надежного укрытия. Вероятность поразить зверюгу ужасного с первого выстрела равна 0,4; с каждым выстрелом она возрастает на 0,1. У стрелка 4 заряда. Х - число выстрелов.
Вариант 4. Комиссар Жюв с помощниками устроили 4 хитроумные ловушки на Фантомаса. Однако Фантомас не прост: первую ловушку он проходит с вероятностью 0,7; для каждой последующей ловушки эта вероятность уменьшается на 0,2. Х - число пройденных злодеем ловушек.
Вариант 5. Остап Бендер играет в шахматы с любителями из Васюков до первого выигрыша. Вероятность выиграть первую партию у любителя равна 0,2; с каждой партией она повышается на 0,2 . Пришло 4 любителя. Х - число сыгранных партий.
Вариант 6. Спасая свою жизнь, Красная Шапочка кормит голодного Волка пирожками. Первым пирожком Волк наедается с вероятностью 0,3; с каждым следующим пирожком эта вероятность увеличивается на 0,1. У девочки 5 пирожков. Х - число съеденных Волком пирожков.
Вариант 7. Колобку по очереди могут встретиться Заяц, Волк, Медведь и Лиса. Вероятность избежать зубов Зайца равна 0,6; с каждым последующим зверем она уменьшается на 0,1. Х - число пройденных Колобком зверей.
Вариант 8. Карлсон решил продолжить знакомство с Малышом, но забыл, в какое из пяти раскрытых окон он влетал накануне. Х - число исследованных Карлсоном комнат.
Вариант 9. По пути в Англию за подвесками королевы Д’Артаньян с мушкетерами вынуждены преодолевать ловушки, устроенные приспешниками кардинала. Первую ловушку они преодолевают с вероятностью 0,8; для каждой последующей эта вероятность уменьшается на 0,2. Всего ловушек 4. Х- число пройденных гасконцем ловушек .
Вариант 10. Четыре капуцина однажды вышли в сад. Тем временем на берегу резвилась русалка, увидеть которую один монах может с вероятностью 0,3. Х - число увидевших речную деву монахов.
Вариант 11. Дядя Федор, Матроскин и Шарик ищут клад по карте с 4-мя подозрительными отметинами. Вероятность обнаружить клад с 1-й попытки равна 0,1; с каждой последующей она увеличивается на 0,2. Х - число попыток.
Вариант 12. В ходе розыска стула с бриллиантами Остапу Бендеру и Воробьянинову осталось проверить 5 стульев. Вероятность найти бриллианты в первом стуле равна 0,6; с каждым последующим стулом возрастает на 0,1. Х - число проверенных стульев.
Вариант 13. В ходе автопробега экипаж «Антилопы Гну» попадает в колдобины на дороге. Первую он преодолевает с вероятностью 0,9; вторую - 0,6, с каждой последующей эта вероятность уменьшается на 0,2. Х - число пройденных колдобин.
Вариант 14. Илья Муромец бьется со Змеем Горынычем. Вероятность сразить Змея первым ударом равна 0,7; с каждым ударом она возрастает на 0,1. Х - число ударов.
Вариант 15. Буратино убегает от лисы Алисы и кота Базилио по ночному лесу. На его пути 4 ямы. Первую он проскакивает с вероятностью 0,7; с каждой последующей она убывает на 0,1. Х - число преодоленных Буратино ям.
Вариант 16. В харчевне «Три пескаря» Буратино на свои 5 золотых угощает лису Алису и кота Базилио. Вероятность накормить компанию на один золотой равна 0,5; с каждым последующим она возрастает на 0,1. Х - число истраченных золотых.
Вариант 17. Х - число попаданий в цель при четырех выстрелах, если вероятность попадания при одном выстреле равна 0,3.
Вариант 18. Во время проведения спортивного мероприятия была организована лотерея. Разыгрывались три предмета: два по цене 200 руб. и один стоимостью 600 руб. Всего было продано 50 билетов по цене 20 руб. Х - сумма чистого выигрыша для участника мероприятия, который приобрел только один билет.
Вариант 19. Во время проведения спортивного мероприятия была организована лотерея. Разыгрывались три предмета: два по цене 200 руб. и один стоимостью 600 руб. Всего было продано 50 билетов по цене 20 руб. Х - сумма чистого выигрыша для участника мероприятия, который приобрел только два билета.
Вариант 20. При некотором технологическом процессе вероятность изготовления нестандартного изделия равна 0,05. Контроль качества изделий происходит следующим образом: берется одно изделие, если оно окажется нестандартным, то проверка прекращается, а партия задерживается, если изделие стандартное, то для проверки берется следующее, и т.д. Всего проверяется не более пяти изделий. Х - число проверяемых изделий.
Вариант 21. В урне имеется четыре шара с номерами от 1 до 4. Вынули два шара. Случайная величина Х - сумма номеров шаров
Вариант 22. Команда состоит из двух стрелков. Числа очков, выбиваемых каждым из них при одном выстреле, являются случайными величинами Х1 и Х2, которые характеризуются следующими законами распределения:
| Х1 | Х2 | ||||||||
| Р | 0,3 | 0,4 | 0,3 | Р | 0,1 | 0,1 | 0,3 | 0,5 |
Результаты стрельбы одного стрелка не влияют на результаты стрельбы второго. Х - число очков, выбиваемых командой, если стрелки сделали по одному выстрелу.
Вариант 23. Охотник стреляет по дичи до второго попадания, успевает сделать не более четырех выстрелов. Х - число промахов, если вероятность попадания в цель при одном выстреле равна 0,7.
Вариант 24. При подготовке к экзамену студенту нужна конкретная книга. Вероятность того, что она в читальном зале свободна равна 0,3. Х - число дней посещения читального зала библиотеки студентом, если до экзамена осталось 4 дня.
Вариант 25. Обрыв связи произошел на одном из пяти звеньев телефонного кабеля. Монтер последовательно проверяет для обнаружения места обрыва. Х - число обследованных звеньев, если вероятность обрыва связи одинакова для всех звеньев.
ЗАДАНИЕ 4
| При измерении напряжения сухих батарей в 6,7% случаев получается значение, превышающее 4,5 В. В то же время 15,9% всех батарей имеют напряжение менее 4,25 В. Вычислить среднее значение и среднее квадратическое отклонение напряжения, предполагая, что распределение нормальное. | |
| На перекрёстке стоит автоматический светофор, в котором 1 минуту горит зелёный свет и 0,5 минут – красный, затем опять зелёный и т.д. Все моменты времени появления у светофора автомашины равновозможны. Построить график функции распределения случайной величины Х – времени ожидания машины у перекрёстка. Найти среднее время ожидания. | |
Время безотказной работы ЭВМ имеет показательное распределение с параметром 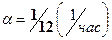 . Какова вероятность того, что за сутки произойдёт хотя бы один отказ? Найти среднее число отказов: а) за сутки; б) за двое суток. Чему равно среднее время безотказной работы ЭВМ? . Какова вероятность того, что за сутки произойдёт хотя бы один отказ? Найти среднее число отказов: а) за сутки; б) за двое суток. Чему равно среднее время безотказной работы ЭВМ?
| |
| Поток сбоев, возникающих при работе ЭВМ, можно считать простейшим. Среднее число сбоев за сутки равно 1,5. Для решения задачи на ЭВМ требуется 16 часов машинного времени, причём при наличии сбоя приходится начинать решение сначала. Какова вероятность того, что для решения задачи потребуется более двух попыток? | |
| Изделие считается высшего качества, если отклонение его размера от номинального не превосходит по абсолютной величине 3,45 мм. Случайные отклонения размера от номинального подчиняются нормальному закону с параметрами а = 0, s = 3 мм. Определить среднее число изделий высшего качества в партии из 400 изделий. | |
| Поток отказов радиоаппаратуры можно считать простейшим. Среднее число отказов за 1000 часов работы равно 5. Определить вероятность отказа радиоаппаратуры за 20 часов работы. Найти среднее время безотказной работы радиоаппаратуры. | |
| Случайная величина Х имеет нормальное распределение. М[Х] = 0, P{–1 < X < 1} = 0,5. Найти среднее квадратическое отклонение случайной величины Х и P{X > 1}. | |
| Поток неисправностей (сбоев), возникающих при работе автоматической линии, можно считать простейшим. Среднее число неисправностей за сутки равно 1,5. Какова вероятность того, что за сутки произойдёт более 3 сбоев? Чему равно среднее время до первой неисправности? | |
Время безотказной работы устройства имеет показательное распределение с параметром 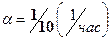 . Какова вероятность того, что за 20 часов работы будет не более 2 отказов? Чему равно среднее число отказов за 40 часов работы? . Какова вероятность того, что за 20 часов работы будет не более 2 отказов? Чему равно среднее число отказов за 40 часов работы?
| |
При исследовании содержания углерода в промышленном газе получено среднее значение 2,4%. В 75% случаев 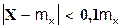 . Считая содержание углерода в промышленном газе нормальной случайной величиной, найти среднее квадратическое отклонение. . Считая содержание углерода в промышленном газе нормальной случайной величиной, найти среднее квадратическое отклонение.
| |
| Аппаратура содержит 2000 одинаково надёжных элементов, надёжность каждого из которых равна 0,9995, а отказы независимы. Какова вероятность отказа аппаратуры, если она выходит из строя лишь при отказе не менее чем двух элементов? Чему равна надёжность аппаратуры? Найти математическое ожидание и среднее квадратическое отклонение числа отказавших элементов за рассматриваемый промежуток времени. | |
| Вероятность выхода из строя изделия за время испытаний на надёжность равна 0,3. Найти вероятность того, что за время испытаний из 100 изделий выйдут из строя: а) не менее 20 изделий; б) ровно 10 изделий. | |
| Какой ширины должно быть поле допуска, чтобы с вероятностью не более 0,0027 получилась деталь с контролируемым размером вне поля допуска, если случайные отклонения размера от середины поля допуска подчиняются нормальному закону с параметрами а = 0, s = 5 мм. | |
| Поток отказов технического устройства можно считать простейшим потоком. Среднее число отказов за 1000 часов работы равно 10. Найти а) среднее время безотказной работы; б) вероятность того, что устройство проработает безотказно не менее 200 часов. | |
| Измерительный прибор имеет систематическую ошибку 5 м и среднюю квадратическую ошибку 75 м. Какова вероятность того, что при трёх измерениях расстояния ошибка хотя бы одного измерения не превзойдёт по абсолютной величине 5 м? | |
| Шкала рычажных весов имеет цену деления 1 г. При измерении массы химических компонентов смеси отсчёт делается с точностью до целого деления с округлением в ближайшую сторону. Какова вероятность, что абсолютная ошибка определения массы не превысит величины среднего квадратического отклонения возможных ошибок определения массы? | |
| Измеряемая случайная величина Х подчиняется нормальному закону распределения с параметрами а = 10, s = 5. Найти симметричный относительно математического ожидания интервал, в который с вероятностью р = 0,9544 попадает измеренное значение. | |
Время безотказной работы радиоэлектронной аппаратуры имеет показательное распределение с параметром 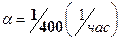 . Найти вероятность того, что за 800 часов работы будет ровно 2 отказа. Чему равно среднее число отказов за 600 часов работы? . Найти вероятность того, что за 800 часов работы будет ровно 2 отказа. Чему равно среднее число отказов за 600 часов работы?
| |
| В нормально распределённой совокупности 15% значений случайной величины меньше 12 и 40% значений больше 16,2. Найти среднее значение и среднее квадратическое отклонение данного распределения. | |
| Для контроля продукции из очень большой партии изделий выбирают случайным образом 100 изделий. Доля брака в партии составляет 15%. Вся партия бракуется, если среди отобранных изделий окажется не менее 10 дефектных. Какова вероятность того, что партия будет забракована? Чему равно среднее число дефектных изделий среди 100 отобранных? | |
| Распределение времени безотказной работы технического устройства можно считать показательным. Из 1000 проверенных изделий 50 изделий проработали более 600 часов. Оценить среднее число отказов за 400 часов. | |
Шарики и подшипники бракуются следующим образом: если шарик проходит через отверстие диаметра d2 , но не проходит через отверстие диаметра d1 < d2 , то шарик считается годным. В противном случае шарик бракуется. Считается, что диаметр шарика распределён по нормальному закону с параметрами 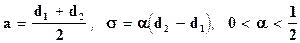 . s определяет точность изготовления шариков. Как следует выбрать a, чтобы брак составлял не более 2% всей продукции? . s определяет точность изготовления шариков. Как следует выбрать a, чтобы брак составлял не более 2% всей продукции?
| |
| Номинальный размер детали – 50 мм, технический допуск ±0,3 мм. Дисперсия (точность) станка, на котором получают данный размер, равна 0,01 мм2. Считая, что закон распределения размера нормальный, определить среднее значение и среднее квадратическое отклонение числа дефектных изделий в партии из 10000 изделий. | |
| Поток неисправностей, возникающих при работе автоматической линии, можно считать простейшим. Среднее число сбоев за сутки 1,5. Какова вероятность того, что до возникновения 1-й неисправности пройдет не менее суток? | |
| Время безотказной работы изделия имеет показательное распределение. Среднее время безотказной работы – 10 000 часов. Найти время безотказной работы, отвечающее вероятности р=0,9 безотказной работы. |
ЗАДАНИЕ 5
Даны результаты пятидесяти измерений непрерывной одномерной случайной величины X.
1. Построить гистограмму выборки.
2. Найти точечные оценки математического ожидания M[X], дисперсии D[X] и среднего квадратического отклонения σ[X]. Для этого вычислить:
1) выборочное среднее 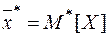 и выборочную дисперсию
и выборочную дисперсию 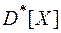 ;
;
2) несмещённую оценку 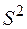 дисперсии и оценку
дисперсии и оценку 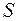 среднего квадратического отклонения.
среднего квадратического отклонения.
3. Предполагая, что случайная величина X имеет нормальное распределение, найти доверительные интервалы с надёжностью 0,9 и 0, 99 для математического ожидания и дисперсии.
4. Проверить гипотезу о нормальности распределения случайной величины X по критерию 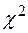 при уровнях значимости 0,05 и 0,01.
при уровнях значимости 0,05 и 0,01.
Вариант 1
Упорядоченная выборка:
-0.012 0.018 0.043 0.057 0.067 0.082 0.101 0.102 0.109 0.110 0.111 0.135 0.158 0.163 0.168 0.180 0.195 0.196 0.197 0.198 0.199 0.200 0.215 0.225 0.232 0.248 0.256 0.260 0.264 0.265 0.270 0.278 0.285 0.289 0.293 0.295 0.299 0.310 0.315 0.317 0.325 0.345 0.371 0.398 0.403 0.471 0.483 0.484 0.537 0.584
Вариант 2
Упорядоченная выборка:
-0.024 0.036 0.086 0.114 0.134 0.164 0.202 0.204 0.218 0.219 0.223 0.271 0.317 0.326 0.336 0.361 0.390 0.392 0.397 0.398 0.399 0.405 0.430 0.450 0.465 0.497 0.512 0.519 0.520 0.529 0.539 0.557 0.569 0.579 0.587 0.589 0.599 0.619 0.629 0.634 0.649 0.691 0.743 0.796 0.806 0.943 0.966 0.968 1.075 1.168
Вариант 3
Упорядоченная выборка:
-0.037 0.054 0.128 0.171 0.201 0.246 0.303 0.306 0.327 0.329 0.334 0.406 0.475 0.489 0.505 0.541 0.585 0.588 0.596 0.597 0.598 0.599 0.645 0.674 0.697 0.745 0.768 0.779 0.780 0.794 0.809 0.835 0.854 0.864 0.880 0.884 0.898 0.929 0.944 0.951 0.974 1.036 1.114 1.194 1.208 1.414 1.450 1.452 1.612 1.752
Вариант 4
Упорядоченная выборка:
-0.049 0.073 0.171 0.228 0.268 0.328 0.403 0.408 0.436 0.439 0.445 0.542 0.634 0.652 0.673 0.721 0.780 0.784 0.794 0.796 0.798 0.799 0.860 0.899 0.930 0.993 1.024 1.039 1.040 1.058 1.078 1.113 1.138 1.139 1.174 1.178 1.197 1.239 1.258 1.268 1.299 1.381 1.485 1.592 1.611 1.885 1.933 1.936 2.149 2.336
Вариант 5
Упорядоченная выборка:
-0.061 0.091 0.214 0.285 0.334 0.410 0.504 0.510 0.545 0.549 0.556 0.677 0.792 0.815 0.841 0.902 0.975 0.980 0.993 0.994 0.997 0.999 1.075 1.124 1.162 1.242 1.279 1.298 1.300 1.323 1.348 1.392 1.423 1.433 1.467 1.473 1.497 1.548 1.573 1.585 1.624 1.727 1.857 1.990 2.014 2.356 2.416 2.420 2.686 2.920
Вариант 6
Упорядоченная выборка:
-0.073 0.109 0.257 0.343 0.401 0.492 0.605 0.612 0.654 0.658 0.668 0.812 0.951 0.978 1.009 1.082 1.169 1.176 1.191 1.193 1.197 1.198 1.290 1.349 1.395 1.490 1.535 1.558 1.560 1.587 1.617 1.670 1.707 1.708 1.761 1.767 1.796 1.858 1.887 1.902 1.948 2.072 2.228 2.388 2.417 2.828 2.899 2.904 3.224 3.504
Вариант 7
Упорядоченная выборка:
-0.085 0.127 0.300 0.400 0.468 0.574 0.706 0.714 0.763 0.768 0.779 0.948 1.109 1.141 1.177 1.262 1.364 1.371 1.390 1.392 1.396 1.398 1.505 1.573 1.627 1.738 1.791 1.818 1.820 1.852 1.887 1.948 1.992 1.993 2.054 2.062 2.095 2.168 2.202 2.219 2.273 2.417 2.600 2.786 2.819 3.299 3.383 3.387 3.761 4.088
Вариант 8
Упорядоченная выборка:
-0.008 0.012 0.027 0.036 0.043 0.052 0.064 0.065 0.069 0.070 0.071 0.086 0.101 0.104 0.107 0.115 0.124 0.125 0.126 0.127 0.128 0.130 0.137 0.143 0.148 0.158 0.163 0.165 0.167 0.168 0.171 0.177 0.181 0.185 0.187 0.188 0.190 0.197 0.200 0.202 0.206 0.220 0.236 0.253 0.256 0.300 0.307 0.308 0.342 0.371
Вариант 9
Упорядоченная выборка:
-0.020 0.030 0.070 0.093 0.109 0.134 0.165 0.167 0.178 0.180 0.182 0.222 0.259 0.267 0.275 0.295 0.319 0.320 0.321 0.325 0.326 0.327 0.352 0.368 0.380 0.406 0.419 0.425 0.427 0.433 0.441 0.455 0.465 0.466 0.480 0.482 0.490 0.507 0.515 0.519 0.531 0.565 0.607 0.651 0.659 0.771 0.790 0.792 0.879 0.955
Вариант 10
Упорядоченная выборка:
-0.032 0.048 0.113 0.150 0.176 0.216 0.266 0.269 0.287 0.289 0.293 0.357 0.418 0.429 0.443 0.475 0.514 0.516 0.523 0.524 0.526 0.527 0.567 0.592 0.613 0.655 0.674 0.684 0.685 0.697 0.710 0.734 0.750 0.754 0.773 0.776 0.789 0.816 0.829 0.836 0.856 0.910 0.979 1.049 1.062 1.242 1.274 1.275 1.416 1.539
Вариант 11
Упорядоченная выборка:
-0.044 0.066 0.156 0.208 0.243 0.298 0.367 0.371 0.396 0.399 0.404 0.492 0.576 0.592 0.611 0.656 0.709 0.712 0.722 0.723 0.725 0.726 0.782 0.817 0.845 0.903 0.930 0.944 0.945 0.962 0.980 1.012 1.034 1.035 1.067 1.071 1.088 1.126 1.144 1.153 1.181 1.256 1.350 1.447 1.464 1.713 1.757 1.759 1.953 2.123
Вариант 12
Упорядоченная выборка:
-0.057 0.084 0.198 0.265 0.310 0.380 0.468 0.473 0.505 0.509 0.516 0.628 0.735 0.755 0.780 0.836 0.904 0.908 0.920 0.922 0.925 0.926 0.997 1.042 1.078 1.151 1.186 1.204 1.206 1.226 1.249 1.290 1.319 1.320 1.360 1.365 1.388 1.436 1.458 1.470 1.505 1.601 1.722 1.845 1.867 2.185 2.240 2.243 2.491 2.707
Вариант 13
Упорядоченная выборка:
-0.069 0.102 0.241 0.322 0.377 0.462 0.568 0.575 0.614 0.619 0.627 0.763 0.893 0.918 0.948 1.016 1.098 1.104 1.119 1.121 1.124 1.126 1.211 1.267 1.310 1.400 1.442 1.463 1.466 1.491 1.519 1.569 1.603 1.604 1.654 1.660 1.687 1.745 1.773 1.787 1.830 1.946 2.093 2.243 2.270 2.656 2.723 2.727 3.028 3.291
Вариант 14
Упорядоченная выборка:
-0.081 0.121 0.284 0.379 0.444 0.544 0.669 0.677 0.723 0.728 0.738 0.899 1.052 1.081 1.116 1.197 1.293 1.300 1.317 1.320 1.324 1.325 1.426 1.492 1.543 1.648 1.698 1.723 1.726 1.756 1.788 1.847 1.888 1.889 1.947 1.955 1.986 2.055 2.087 2.104 2.155 2.292 2.464 2.641 2.673 3.127 3.207 3.211 3.565 3.875
Вариант 15
Упорядоченная выборка:
-0.003 0.005 0.012 0.016 0.018 0.022 0.027 0.028 0.031 0.032 0.034 0.037 0.043 0.044 0.046 0.049 0.050 0.051 0.052 0.053 0.054 0.056 0.058 0.061 0.063 0.067 0.069 0.070 0.071 0.072 0.073 0.076 0.077 0.078 0.079 0.080 0.081 0.084 0.085 0.086 0.088 0.094 0.101 0.108 0.109 0.128 0.131 0.139 0.146 0.159
Вариант 16
Упорядоченная выборка:
-0.016 0.023 0.054 0.073 0.085 0.104 0.128 0.130 0.139 0.140 0.141 0.172 0.202 0.207 0.214 0.229 0.248 0.249 0.252 0.253 0.254 0.256 0.273 0.286 0.296 0.316 0.325 0.330 0.331 0.336 0.343 0.354 0.362 0.369 0.373 0.375 0.381 0.394 0.400 0.403 0.413 0.439 0.472 0.506 0.512 0.599 0.614 0.615 0.683 0.743
Вариант 17
Упорядоченная выборка:
-0.028 0.041 0.097 0.130 0.152 0.186 0.229 0.232 0.248 0.249 0.253 0.308 0.360 0.370 0.382 0.410 0.443 0.445 0.451 0.452 0.4
|
из
5.00
|
Обсуждение в статье: РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы