Молекулярная физика и термодинмика

№1
Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.
По эквивалентной формулировке идеальный газ - такой газ, который одновременно подчиняется закону Бойля — Мариотта и Гей-Люссака^[7], то есть:

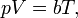
где — давление, — абсолютная температура. Свойства идеального газа описываются уравнением Менделеева — Клапейрона

,

где - универсальная газовая постоянная, — масса, — молярная масса.

или

где — концентрация частиц, — постоянная Больцмана.

Для любого идеального газа справедливо соотношение Майера:

где — универсальная газовая постоянная, 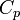— молярная теплоемкость при постоянном давлении, — молярная теплоемкость при постоянном объёме.

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

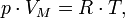
где

• — давление,
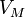• — молярный объём,
• — универсальная газовая постоянная
• — абсолютная температура,К.

Так как , где — количество вещества, а , где — масса, — молярная масса, уравнение состояния можно записать:

Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.

В случае постоянной массы газа уравнение можно записать в виде:

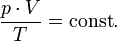
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:

— закон Бойля — Мариотта.

— Закон Гей-Люссака.

— закон Шарля (второй закон Гей-Люссака, 1808 г.)

А в форме пропорции этот закон удобен для расчёта перевода газа из одного состояния в другое.

№2
Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление, объём илитемпература — остаются неизменными. Так, неизменному давлению соответствует изобарный процесс, объёму — изохорный, температуре — изотермический, энтропии —изоэнтропийный (например, обратимый адиабатический процесс). Линии, изображающие данные процессы на какой-либо термодинамической диаграмме, называются изобара, изохора,изотерма и адиабата соответственно. Изопроцессы являются частными случаями политропного процесса.
Изобарный процесс

Основная статья: Изобарный процесс

Графики изопроцессов в различных системах координат

Изобарный процесс (др.-греч. ισος, isos — «одинаковый» + βαρος, baros — «вес») — процесс изменения состояния термодинамической системы при постоянном давлении ( )

Зависимость объёма газа от температуры при неизменном давлении была экспериментально исследована в 1802 году Жозефом Луи Гей-Люссаком. Закон Гей-Люссака: При постоянном давлении и неизменных значениях массы газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным: V/T = const.

[править]Изохорный процесс

Основная статья: Изохорный процесс

Изохорный процесс (от греч. хора — занимаемое место) — процесс изменения состояния термодинамической системы при постоянном объёме ( ). Для идеальных газов изохорический процесс описывается законом Шарля: для данной массы газа при постоянном объёме, давление прямо пропорционально температуре:

Линия, изображающая изохорный процесс на диаграмме, называется изохорой.

Ещё стоит указать что поданная к газу энергия расходуется на изменение внутренней энергии то есть Q = 3* ν*R*T/2=3*V*ΔP, где R — универсальная газовая постоянная, ν количество молей в газе, T температура в Кельвинах, V объём газа, ΔP приращение изменения давления. а линию, изображающая изохорный процесс на диаграмме, в осях Р(Т), стоит продлить и пунктиром соединить с началом координат, так как может возникнуть недопонимание.

[править]Изотермический процесс

Основная статья: Изотермический процесс

Изотермический процесс (от греч. «термос» — тёплый, горячий) — процесс изменения состояния термодинамической системы при постоянной температуре ( )( )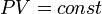. Изотермический процесс описывается законом Бойля — Мариотта:

При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным: PV = const.

№3
Молекулярно-кинетическая теория (сокращённо МКТ) — теория XIX века, рассматривавшая строение вещества, в основном газов, с точки зрения трёх основных приближенно верных положений:

• все тела состоят из частиц: атомов, молекул и ионов;
• частицы находятся в непрерывном хаотическом движении (тепловом);
• частицы взаимодействуют друг с другом путём абсолютно упругих столкновений.

, где k является постоянной Больцмана (отношение универсальной газовой постоянной R к числу Авогадро N_A), i — число степеней свободы молекул ( в большинстве задач про идеальные газы, где молекулы предполагаются сферами малого радиуса, физическим аналогом которых могут служить инертные газы), а T - абсолютная температура.

Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) газовой системы с микроскопическими (масса молекул, средняя скорость их движения).

№5
Длина свободного пробега молекулы — это среднее расстояние (обозначаемое ), которое частица пролетает за время свободного пробега от одного столкновения до следующего.

Длина свободного пробега каждой молекулы различна, поэтому в кинетической теории вводится понятие средней длины свободного пробега (<λ>). Величина <λ> является характеристикой всей совокупности молекул газа при заданных значениях давления и температуры.
, где — эффективное сечение молекулы, — концентрация молекул.
В термодинамически неравновесных системах происходят особые необратимые процессы, называемые явлениями переноса, в результате которых осуществляется пространственный перенос массы, импульса, энергии. К явлениям переноса относятсятеплопроводность (перенос энергии), диффузия (перенос массы) и внутреннее трение (перенос импульса). Ограничимся одномерными явлениями переноса. Систему отсчета будем выберать так, чтобы ось х была направлена в сторону в направления переноса.
Ва́куум (от лат. vacuum — пустота) — пространство, свободное от вещества. В технике и прикладной физике под вакуумом понимают среду, содержащую газ придавлениях значительно ниже атмосферного. Вакуум характеризуется соотношением между длиной свободного пробега молекул газа λ и характерным размером среды d. Под d может приниматься расстояние между стенками вакуумной камеры, диаметр вакуумного трубопровода и т. д. В зависимости от величины соотношения λ/d различают низкий ( ), средний ( ) и высокий ( ) вакуум.
№6
Распределение Ма́ксвелла — распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию. Распределение Максвелла также применимо для электронных процессов переноса и других явлений. Распределение Максвелла применимо к множеству свойств индивидуальных молекул в газе. О нём обычно думают как о распределении энергий молекул в газе, но оно может также применяться к распределению скоростей, импульсов, и модуля импульсов молекул. Также оно может быть выражено как дискретное распределение по множеству дискретных уровней энергии, или как непрерывное распределение по некоторому континууму энергии.

Распределение Максвелла может быть получено при помощи статистической механики (см. происхождение статсуммы). Как распределение энергии, оно соответствует самому вероятному распределению энергии, в столкновительно-доминируемой системе, состоящей из большого количества невзаимодействующих частиц, в которой квантовые эффекты являются незначительными. Так как взаимодействие между молекулами в газе является обычно весьма небольшим, распределение Максвелла даёт довольно хорошее приближение ситуации, существующей в газе.

Во многих других случаях, однако, даже приблизительно не выполнено условие доминирования упругих соударений над всеми другими процессами. Это верно, например, в физикеионосферы и космической плазмы, где процессы рекомбинации и столкновительного возбуждения (то есть излучательные процессы) имеют большое значение, в особенности для электронов. Предположение о применимости распределения Максвелла дало бы в этом случае не только количественно неверные результаты, но даже предотвратило бы правильное понимание физики процессов на качественном уровне. Также, в том случае где квантовая де Бройлева длина волны частиц газа не является малой по сравнению с расстоянием между частицами, будут наблюдаться отклонения от распределения Максвелла из-за квантовых эффектов.

Распределение энергии Максвелла может быть выражено как дискретное распределение энергии:

,

где является числом молекул имеющих энергию при температуре системы , является общим числом молекул в системе и — постоянная Больцмана. (Отметьте, что иногда вышеупомянутое уравнение записывается с множителем , обозначающим степень вырождения энергетических уровней. В этом случае сумма будет по всем энергиям, а не всем состояниям системы). Поскольку скорость связана с энергией, уравнение (1) может использоваться для получения связи между температурой и скоростями молекул в газе. Знаменатель в уравнении (1) известен как каноническая статистическая сумма.

№7

Первым экспериментальным подтверждением существования распределения молекул по скоростям можно считать результаты опыта Штерна, описанного в параграфе 2.3. Но точность этого опыта была недостаточной для установления конкретного вида распределения.

Прямые измерения скорости атомов ртути в пучке были выполнены в 1929 году Ламмертом. Упрощенная схема этого эксперимента показана на рис. 5.6.

Рис. 5.6.

Схема опыта Ламмерта

1 - быстро вращающиеся диски, 2 - узкие щели, 3 - печь, 4 - коллиматор, 5 - траектория молекул, 6 - детектор

Два диска 1, насаженные на общую ось, имели радиальные прорези 2, сдвинутые друг относительно друга на угол . Напротив щелей находилась печь 3, в которой нагревался до высокой температуры легкоплавкий металл. Разогретые атомы металла, в данном случае ртути, вылетали из печи и с помощью коллиматора 4 направлялись в необходимом направлении. Наличие двух щелей в коллиматоре обеспечивало движение частиц между дисками по прямолинейной траектории 5, параллельной их оси. В установке Ламмерта в дисках было сделано множество щелей (они на рисунке не изображены) с целью увеличения интенсивности прошедшего пучка. Далее атомы, прошедшие прорези в дисках, регистрировались с помощью детектора 6. Вся описанная установка помещалась в глубокий вакуум.

При вращении дисков с постоянной угловой скоростью , через их прорези беспрепятственно проходили только атомы, имевшие скорость :

, (5.75)

где - расстояние между вращающимися дисками.

Изменяя угловую скорость вращения дисков можно было отбирать из пучка молекулы, имеющие определенную скорость , и по регистрируемой детектором интенсивности судить об относительном содержании их в пучке.

Таким способом удалось экспериментально проверить статистический закон распределения молекул по скоростям. Позже, когда при создании ядерного оружия возникла необходимость выделения нейтронов с определенной кинетической энергией, подобная схема была применена в устройстве, названным нейтронным монохроматором, позволяющим получать энергетические спектры нейтронов.

Несколько иначе был организован эксперимент по определению распределения по скоростям для атомов цезия, выполненный в 1947 году немецким физиком-экспериментатором Иммануэлем Эстерманом (1900 - 1973) совместно с О. Симпсоном и Штерном. На рис. 5.7. приведено схематическое изображение опыта Эстермана. Пучок атомов цезия вылетал через отверстие в печи 1 с некоторой скоростью и под действием силы тяжести начинал двигаться по параболе. Атомы, прошедшие через узкую щель в диафрагме 2, улавливались детектором 3, который можно было располагать на различных высотах .

Схема опыта Эстермана

1 - печь, 2 - диафрагма с узкой щелью, 3 - детектор

Величина отклонения пучка в гравитационном поле Земли зависела от скорости атома. В этих опытах отклонение составляло величину порядка нескольких долей миллиметра при расстоянии от печи до детектора равном 2 метрам. Перемещая датчик и регистрируя количество атомов цезия, попадающих в детектор за единицу времени, можно было построить зависимость интенсивности пучка от величины . Последующий пересчет, с учетом известной зависимости высоты от скорости атома , давал распределение по скоростям атомов цезия.

Все проведенные эксперименты подтвердили справедливость полученного Максвеллом распределения по скоростям для атомных и молекулярных пучков.
№7
Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести.

Для идеального газа, имеющего постоянную температуру и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения одинаково), барометрическая формула имеет следующий вид:

где — давление газа в слое, расположенном на высоте , 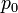— давление на нулевом уровне ( ), — молярная масса газа, — газовая постоянная, — абсолютная температура. Из барометрической формулы следует, что концентрация молекул (или плотность газа) убывает с высотой по тому же закону:

С уменьшением температуры число молекул на высотах, отличных от нуля, убывает. При T = 0 тепловое движение прекращается, все молекулы расположились бы на земной поверхности. При высоких температурах, наоборот, молекулы оказываются распределёнными по высоте почти равномерно, а плотность молекул медленно убывает с высотой. Так как mgh– это потенциальная энергия U, то на разных высотах U = mgh – различна. Следовательно, (2.5.2) характеризует распределение частиц по значениям потенциальной энергии:

,

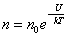(2.5.3)

– это закон распределения частиц по потенциальным энергиям – распределение Больцмана. Здесь n₀ – число молекул в единице объёма там, где U = 0.

№8
Если система обменивается теплом с окружающими телами и совершает работу (положительную или отрицательную), то изменяется состояние системы, т. е. изменяются ее макроскопические параметры (температура, давление, объем). Так как внутренняя энергия U однозначно определяется макроскопическими параметрами, характеризующими состояние системы, то отсюда следует, что процессы теплообмена и совершения работы сопровождаются изменением ΔU внутренней энергии системы.

Первый закон термодинамики является обобщением закона сохранения и превращения энергии для термодинамической системы. Он формулируется следующим образом:

Изменение ΔU внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q, переданной системе, и работой A, совершенной системой над внешними телами.

Соотношение, выражающее первый закон термодинамики, часто записывают в другой форме: