 |
Главная |
Раздел: Дифференциальное исчисление функции одной переменной
|
из
5.00
|
1. Производная функции равна
а) отношению дифференциала функции к дифференциалу переменной;
б) произведению дифференциала функции на дифференциал переменной;
в) сумме дифференциала функции и дифференциала переменной.
2. Дифференциал функции приближенно равен
а) приращению аргумента;
б) приращению функции;
в) отношению приращению функции к приращению аргумента.
3. Вычислить производную функции  .
.
4. Найти производную функции 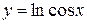 .
.
5. Найти производную функции, заданной параметрически,
 .
.
6. Найти вторую производную функции  .
.
7. Найти уравнение касательной к графику функции  .
.
8. Если функция возрастает на некотором интервале, то ее производная на интервале а) больше нуля; б) меньше нуля; в) равна нулю.
9. В точках возможного экстремума производная функции а) равна нулю; б) равна нулю или не существует; в) не равна нулю.
10. Сколько экстремумов имеет функция  .
.
11. Найти максимальное значение функции  .
.
12. Найти наибольшее значения функции 
на отрезке [0;3].
13. В точках возможного перегиба графика функции ее вторая производная а) равна нулю; б) равна нулю или не существует; в) не равна нулю.
14. График функции имеет выпуклость вниз (вогнутость) на некотором интервале, если вторая производная функции а) больше нуля;
б) равна нулю; в) меньше нуля.
15. Сколько точек перегиба имеет график функции  .
.
16. Найти абсциссу точки перегиба графика функции  .
.
Контроль самостоятельной работы студентов
ТЕСТЫ
Составитель: Голечков Ю.И., д.ф.-м.н., доц.
Раздел: Введение в математический анализ
1. Указать общий член последовательности  :
:
2. Найти ограниченную сверхупоследовательность, заданную общим членом:
а) аn = 2п + 1, б) аn = п, в) аn =  , г) аn =
, г) аn = 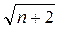 , д) аn = (–1)п.
, д) аn = (–1)п.
3. Найти предел последовательности аn =  :
:
4. Указать первый замечательный предел:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  .
.
5. Найти предел функции слева  :
:
6. Найти предел  :
:
7. Указать бесконечно малую функцию:
а)  при x→2; б) (х
при x→2; б) (х 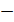 1)2 при х→1; в) tg x при x→
1)2 при х→1; в) tg x при x→  ; г) ln x при x→0+0; д) x2 при x→∞ .
; г) ln x при x→0+0; д) x2 при x→∞ .
8. Указать бесконечно большую функцию:
а) sin x при х→0; б) (х 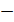 3)2 при х→3; в) 1
3)2 при х→3; в) 1 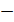 cos x при х→0;
cos x при х→0;
г)  при х→∞; д) ln x при x→+∞.
при х→∞; д) ln x при x→+∞.
9. Найти предел  , заменяя бесконечно малые и бесконечно
, заменяя бесконечно малые и бесконечно
большие функции эквивалентными:
10. Указать необходимое и достаточное условие непрерывности функции f(х) в точке х0:
а)  f(x) ≠
f(x) ≠  f(x) ≠ f(x0); б)
f(x) ≠ f(x0); б)  f(x) =
f(x) =  f(x) ≠ f(x0);
f(x) ≠ f(x0);
в)  f(x) =
f(x) =  f(x); г)
f(x); г)  f(x) =
f(x) =  f(x) = f(x0);
f(x) = f(x0);
д)  f(x) ≠ f(x0).
f(x) ≠ f(x0).
11. Найти интервал непрерывности функции f(х) = (х + 1)(х – 2):
12. Функция f(х) называется непрерывной в точке х0 слева, если:
а)  f(x) = f(x0); б)
f(x) = f(x0); б)  f(x) =
f(x) =  f(x) ≠ f(x0);
f(x) ≠ f(x0);
в)  f(x) =
f(x) =  f(x) = f(x0); г)
f(x) = f(x0); г)  f(x) = f(x0);
f(x) = f(x0);
д)  f(x) ≠
f(x) ≠  f(x) = f(x0).
f(x) = f(x0).
13. Найти точку х0 устранимого разрыва функции f(х) =  :
:
14. Найти точку х0 скачка функции f(х) =  и его величину h:
и его величину h:
15. Найти точки разрыва I-го и II-го рода функции
у = f(х) = 

16. Используя свойства функций, непрерывных на отрезке, найти точки, в которых функция у = х2 – 1  х
х  [–2, 2] обращается в нуль:
[–2, 2] обращается в нуль:
|
из
5.00
|
Обсуждение в статье: Раздел: Дифференциальное исчисление функции одной переменной |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

