 |
Главная |
Оценка достоверности результатов исследования
|
из
5.00
|
Величина того или иного признака неодинакова у всех членов совокупности, несмотря на ее относительную однородность. Например, в группе людей, однородной по возрасту, полу и месту жительства, рост и вес каждого человека отличается от роста и веса других людей. В этом проявляется разнообразие, колеблемость признака в изучаемой совокупности, а значит и средняя арифметическая величина находится в зависимости от колеблемости вариационного ряда. Чем меньше колеблемость ряда, то есть чем меньше амплитуда колебания ряда (разность между самой большой и самой малой вариантой), тем более точно его будет характеризовать средняя арифметическая.
Наиболее полную характеристику разнообразию признака в совокупности, степень варьирования вариационного ряда, дает так называемое среднее квадратическое отклонение, обозначаемое греческой буквой «сигма» - d.
Существует два способа расчёта среднего квадратического отклонения: среднеарифметический и способ моментов.
При среднеарифметическом способе расчёта применяется формула:
 , где
, где
d – истинное отклонение варианты от истинной средней (v-M).
Эта формула используется при небольшом числе наблюдений (n £ 30; р=1). При достаточно большом числе наблюдений (n>30; р>1) определяется средневзвешенное квадратическое отклонение по формуле:
 , где
, где
åd2p – сумма произведения квадрата отклонения на частоту каждой варианты.
По способу моментов расчет среднего квадратического отклонения производится по формуле:

 , где
, где
а – условное отклонение варианты от условной средней (а=v-А);
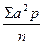 - момент второй степени (при n>30);
- момент второй степени (при n>30);
 - момент первой степени, возведенный в квадрат.
- момент первой степени, возведенный в квадрат.
При числе наблюдений, равном 30 и менее, в момент второй степени n заменяется на (n-1).
Описанные способы расчета среднего квадратического отклонения требуют значительной вычислительной работы. Поэтому можно использовать приближенный способ вычисления среднего квадратичного отклонения по амплитуде вариационного ряда, с использованием формулы:
 , где
, где
А – коэффициент для определения d, соответствующий числу наблюдений (табл.15).
Таблица 15
Определение среднего квадратического отклонения по амплитуде
| Число наблюдений, n | Коэффициент для сигмы, А | Число наблюдений, n | Коэффициент для сигмы, А | Число наблюдений, n | Коэффициент для сигмы, А |
| - 1,13 1,69 2,06 2,33 2,53 2,70 2,85 2,97 3,08 | 4,14 4,19 4,24 4,28 4,32 | 5,98 6,00 6,02 6,06 6,09 | |||
| 4,50 4,64 4,76 4,85 4,94 | 6,12 6,13 6,14 6,17 6,18 | ||||
| 3,17 3,26 3,34 3,41 3,47 3,53 3,59 3,64 3,69 3,74 | 5,01 5,15 5,26 5,35 5,43 5,50 | 6,21 6,23 6,26 6,27 6,28 | |||
| 5,57 5,61 5,68 5,72 5,77 | 6,33 6,34 6,37 6,43 6,47 | ||||
| 3,82 3,90 3,96 4,03 4,09 | 5,80 5,84 5,88 5,92 5,94 | 6,48 |
Помимо среднего квадратического отклонения (d), существует еще один критерий, характеризующий уровень разнообразия величин признака в совокупности, – коэффициент вариации (Cv), который является относительной мерой разнообразия, так как исчисляется как процентное отношение d к средней арифметической величине (М) и высчитывается по формуле:

Для ориентировочной оценки степени разнообразия признака в практике пользуются следующими градациями коэффициента вариации: если коэффициент составляет более 20%, то говорят о сильном разнообразии; при 20-10%-среднее разнообразие; если же коэффициент менее 10%- то считается, что разнообразие слабое.
Коэффициент вариации применяют при сравнении степени разнообразия признаков, имеющих различия в величине признаков или неодинаковую их размерность. Например, если необходимо сравнить степень разнообразия массы тела у новорожденных и 7-летних детей. Ясно, что у новорожденных d всегда будет меньше, чем у 7-летних детей, так как их индивидуальная масса меньше (табл. 16).
Таблица 16
| Группа детей (мальчики) | Средняя масса (М), кг | d, кг | Сv, (%) |
| Новорожденные | 3,5 | ±0,35 | |
| 7-летние | 24,7 | ±3,88 | 15,7 |
Как видно из таблицы 16, в этом случае для определения различия в степени разнообразия необходимо ориентироваться не на среднее квадратическое отклонение (d), а на относительную меру разнообразия – коэффициент вариации (Сn).
Кроме того, коэффициент вариации имеет большое значение для оценки и сопоставления степени разнообразия нескольких признаков с разной размерностью. Например, из данных таблицы 17 видно, что по среднему квадратическому отклонению нельзя судить о различии в степени разнообразия указанных признаков.
Таблица 17
Сравнение различных признаков совокупности по M,d и Сn.
| Признак | М | d | Сv, (%) |
| Общий белок сыворотки крови | 68г/л | ±4 г/л | 5,8 |
| СОЭ | 9 мм/час | ±2 мм/час | 22,0 |
| Лейкоциты | 8000/мм3 | ±800 | 10,0 |
Только Сn позволяет сделать вывод, что наиболее разнообразным признаком в данном примере является СОЭ и менее разнообразным - общий белок крови.
Среднее квадратическое отклонение связано со структурой ряда распределения признака. Теорией статистики доказано, что при нормальном распределении в пределах М±d находится 68% всех случаев, в пределах М±2d - 95,5% всех случаев и в пределах М±3d - 99,7% всех случаев, составляющих совокупность, т.е. охватывает почти весь вариационный ряд (рис.2)

Рис.2 Теоретическая кривая распределения вариант в однородном вариационном ряду по сигмальным отклонениям (кривая Гаусса).
Это теоретическое положение статистики о закономерностях структуры ряда имеет огромное значение для практического применения среднего квадратического отклонения, особенно при разработке проблемы нормы и патологии. Так, в медицине (в здравоохранении) интервал М±d обычно принимается за пределы нормы.
Если при исследовании выясняется, что индивидуальные измерения находятся в пределах 95,5% всех наблюдений, т.е. стандартное отклонение от средней (М) составляет ±2d, то можно говорить о принадлежности исследуемого признака к фактору риска. В этом случае врач должен взять исследуемого пациента под диспансерное наблюдение, а в случае, когда стандартное отклонение от средней (М) составляет ±3d врач должен направить исследуемого на консультацию к специалисту по выявленному признаку у данного индивидуума. Таким образом, среднее квадратическое отклонение является стандартным отклонением, позволяющим предвидеть вероятность появления первых признаков формирования патологии у пациента.
Кроме того, по среднему квадратическому отклонению можно определить коэффициент вариации при сравнении степени разнообразия разных признаков в одной совокупности или однородных признаков в разных совокупностях; определить структуру вариационного ряда; судить о типичности средней арифметической; оценить отдельные признаки у каждого индивидуума по стандартному отклонению t; определить ошибку средней арифметической величины mM (ошибки репрезентативности).
|
из
5.00
|
Обсуждение в статье: Оценка достоверности результатов исследования |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

