Статистические оценки параметров распределения. Состоятельность и несмещенность статистических оценок

Выборочные характеристики

Пусть для изучения генеральной совокупности относительно количественного признака X извлечена выборка объема n.

Выборочным средним называют среднее арифметическое значение признака выборочной совокупности. Если все значения признака выборки объема n различны, то:

.

Если значения признака имеют частоты соответственно, причем , то:

.

Для охарактеризования рассеяния наблюдаемых значений количественного признака выборки вокруг среднего значения вводится выборочная дисперсия. Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения . Если все значения признака выборки объема n различны, то:

.

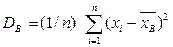Если значения признака имеют частоты соответственно, причем , то:

.

Аналогично выборочным среднему и дисперсии определяются генеральные среднее и дисперсия, характеризующие генеральную совокупность в целом. Для расчета этих характеристик достаточно в вышеприведенных соотношениях заменить объем выборки n на объем генеральной совокупности N.

Фундаментальное значение для практики имеет нахождение среднего и дисперсии признака генеральной совокупности по соответствующим известным выборочным параметрам. Можно показать, что выборочное среднее является несмещенной состоятельной оценкой генерального среднего. В то же время, несмещенной состоятельной оценкой генеральной дисперсии оказывается не выборочная дисперсия , а так называемая «исправленная» выборочная дисперсия, равная .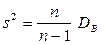

Таким образом, в качестве оценок генерального среднего и дисперсии в математической статистике принимают выборочное среднее и исправленную выборочную дисперсию.

Средним квадратичным отклонением является .

Коэффициентом вариации наз. Процентное отношение среднего квадратического отклонения к средней арифметической .

Начальный момент к-го порядка

Центральный момент к-го порядка

Мода- варианта,имеющая наибольшую частоту

Медиана- это значение признака, находящегося в середине ряда.Для нахождения медианы в дискретном ряде первоначальную сумму частот делят пополам и к полученному результату добавляют 0,5.

Статистическое оценивание

Статистические оценки параметров распределения. Состоятельность и несмещенность статистических оценок

Пусть требуется изучить некоторый количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак и необходимо оценить параметры, которыми оно определяется. Например, если изучаемый признак распределен в генеральной совокупности нормально, то нужно оценить математическое ожидание и среднее квадратическое отклонение; если признак имеет распределение Пуассона – то необходимо оценить параметр l.

Обычно имеются лишь данные выборки, например значения количественного признака , полученные в результате n независимых наблюдений. Рассматривая как независимые случайные величины можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения – это значит найти функцию от наблюдаемых случайных величин, которая дает приближенное значение оцениваемого параметра. Например, для оценки математического ожидания нормального распределения роль функции выполняет среднее арифметическое:

Для того чтобы статистические оценки давали корректные приближения оцениваемых параметров, они должны удовлетворять некоторым требованиям, среди которых важнейшими являются требования несмещенности и состоятельности оценки.

Пусть – статистическая оценка неизвестного параметра теоретического распределения. Пусть по выборке объема n найдена оценка . Повторим опыт, т.е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным получим другую оценку . Повторяя опыт многократно, получим различные числа . Оценку можно рассматривать, как случайную величину, а числа – как ее возможные значения.

Если оценка дает приближенное значение с избытком, т.е. каждое число больше истинного значения то, как следствие, математическое ожидание (среднее значение) случайной величины больше, чем :

.

Аналогично, если дает оценку с недостатком, то .

Таким образом, использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, привело бы к систематическим (одного знака) ошибкам. Если, напротив, , то это гарантирует от систематических ошибок.

Несмещенной называют статистическую оценку , математическое ожидание которой равно оцениваемому параметру при любом объеме выборки .

Смещенной называют оценку, не удовлетворяющую этому условию.

Несмещенность оценки еще не гарантирует получения хорошего приближения для оцениваемого параметра, так как возможные значения могут быть сильно рассеяны вокруг своего среднего значения, т.е. дисперсия может быть значительной. В этом случае найденная по данным одной выборки оценка, например , может оказаться значительно удаленной от среднего значения , а значит, и от самого оцениваемого параметра.

Эффективной называют статистическую оценку, которая, при заданном объеме выборки n, имеет наименьшую возможную дисперсию.

При рассмотрении выборок большого объема к статистическим оценкам предъявляется требование состоятельности.

Состоятельной называется статистическая оценка, которая при n®¥ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при n®¥ стремится к нулю, то такая оценка оказывается и состоятельной.