 |
Главная |
Оценка уравнения множественной линейной регрессии
|
из
5.00
|
Определение выборочного аналога уравнения регрессии имеет смысл только для тех признаков, множественные коэффициенты корреляции которых значимы. Таким образом, согласно полученным результатам проверки соответствующих гипотез, оценивать следует уравнение регрессии Z на (X, Y):
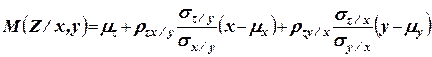 .
.
Выборочные условные средние квадратические отклонения
 ;
;  ;
;
 ;
; 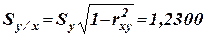 .
.
Выборочные частные коэффициенты регрессии
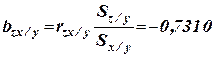 ;
;  .
.
Выборочное уравнение регрессии
 .
.
В данном случае

или
 .
.
Общий вывод
Результаты выполненного корреляционного анализа показывают, что признак Z имеет статистически значимую умеренную связь как с двумерным массивом признаков X, Y, так и с каждым из этих признаков в отдельности, что дает основание для перехода ко второму этапу статистического исследования - построению регрессионной модели, т.е. выявлению той конкретной математической зависимости переменной Z от переменных X, Y, которой наилучшим, в определенном смысле этого слова, образом отвечают имеющиеся статистические данные.
II. Регрессионный анализ
Постановка задачи
Требуется по указанным выше статистическим данным n=14 стран произвести регрессионный анализ зависимости уровня смертности от средней продолжительность жизни женщин и уровня рождаемости.
Трехмерная линейная модель регрессии
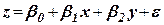 ,
,
где
x, y, z - соответственно значения предикторов X, Y и критериальной переменной Z;
β0, β1, β2 – неизвестные параметры модели;
ε – остаточная компонента (возмущение), численно характеризующей случайность в изменении значения переменной Y.
Установление оценок параметров исходной модели регрессионного анализа
с помощью метода наименьших квадратов
Статистической мерой остаточной компоненты ε в методе наименьших квадратов служит сумма квадратов отклонений действительных (экспериментальных) значений критериальной переменной от соответствующих теоретических (расчетных) значений. Выбираются такие значения параметров модели, при которых данная сумма квадратов будет наименьшей.
Вектор  - несмещенная МНК-оценка параметров
- несмещенная МНК-оценка параметров  - находится по формуле:
- находится по формуле:  .
.
В рассматриваемом случае матрицы  ,
,  ,
,  имеют вид:
имеют вид:

Определение вектора  осуществляется следующим образом.
осуществляется следующим образом.
1. Находится произведение матриц  ,
,  :
:
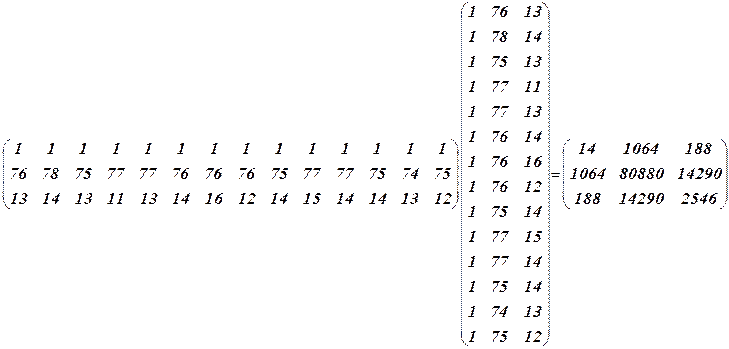
2. Вычисляется произведение матриц  :
:

3. Определяется матрица, обратная к матрице  :
:
 .
.
4. Находится вектор  МНК-оценок параметров
МНК-оценок параметров  модели:
модели:
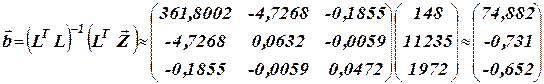 .
.
Итак,
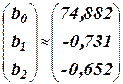 .
.
Следовательно, выборочное уравнение линейной регрессии представимо в виде
 .
.
|
из
5.00
|
Обсуждение в статье: Оценка уравнения множественной линейной регрессии |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

