 |
Главная |
Исследование функции на четность и на периодичность
|
из
5.00
|
Правило Лопиталя. исследование Функции.
Правило Лопиталя расскрытия неопределенностей.
Теорема (правило Лопиталя).
Если  или
или  (то есть, если предел отношения
(то есть, если предел отношения  в точке
в точке  приводит к неопределенности вида
приводит к неопределенности вида 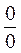 или
или  ) и предел
) и предел  существует, то
существует, то
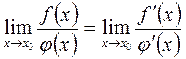 .
.
Пример 1: 
Пример 2:
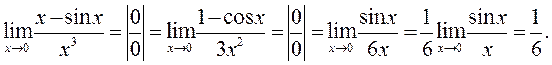
Пример 3: 
Замечание:
1) Неопределенности вида 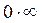 или
или  можно раскрыть по правилу Лопиталя, предворительно преобразовав их к виду
можно раскрыть по правилу Лопиталя, предворительно преобразовав их к виду  или
или  .
.
Пример 4: 
Пример 5:
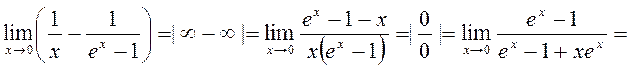

Пример 6: 
 Таким образом,
Таким образом,  .
.
Полное исследование функции
Полное исследование функции проводится по следующей схеме:
1. Нахождение области определения функции;
2. Нахождение точек разрыва, вертикальных и горизонтальных асимптот графика функции;
3. Нахождение (по возможности) точек пересечения графика функции  с осями координат;
с осями координат;
4. Исследование функции на четность и на периодичность;
5. Нахождение интервалов монотонности и экстремумов функции;
6. Нахождение интервалов выпуклости, вогнутости и точек перегиба графика функции;
7. Нахождение наклонной асимптоты графика функции;
8. Построение графика функции.
Пример 7:Исследовать функцию  и построить ее график.
и построить ее график.
Нахождение области определения функции
Если функция задана только законом соответствия

(то есть область определения не указана), то за область определения функции берется множество  {
{  имеет смысл}.
имеет смысл}. 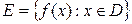 - область изменения (множество значений) функции.
- область изменения (множество значений) функции.
1. Область определения функции:  {
{  имеет смысл}
имеет смысл}  .
.
Нахождение точек разрыва, вертикальных и горизонтальных асимптот графика функции.
По определению непрерывности функции в точке, функция  будет непрерывной в точке
будет непрерывной в точке  , если
, если  .
.
Если в точке  функция не определена или не является непрерывной ( то есть не выполняется равенство
функция не определена или не является непрерывной ( то есть не выполняется равенство  ),
),
то точка  называется точкой разрыва.
называется точкой разрыва.
Так как функция  является элементарной, то она непрерывна в своей области определения, то есть в интервалах
является элементарной, то она непрерывна в своей области определения, то есть в интервалах
 и
и  .
.  - точка разрыва.
- точка разрыва.
Находим пределы функции на концах интервалов  и
и  :
:

 Точка
Точка  - точка разрыва II рода и прямая
- точка разрыва II рода и прямая  является вертикальной асимптотой графика функции при
является вертикальной асимптотой графика функции при  и
и  ;
;


функция не имеет горизонтальную асимптоту.
3. Нахождение (по возможности) точек пересечения графика функции  с осями координат
с осями координат
Для нахождения точки пересечения графика функции  с осью Ох пологаем
с осью Ох пологаем  , а для нахождения точки пересечения с осью Оу полагаем х=0:
, а для нахождения точки пересечения с осью Оу полагаем х=0:
 ,следовательно
,следовательно 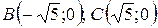 - точка пересечения графика с осью Ох;
- точка пересечения графика с осью Ох;
 , следовательно
, следовательно  - точка пересечения графика с осью Оу.
- точка пересечения графика с осью Оу.
Исследование функции на четность и на периодичность
Функция  называется четной (нечетной), если имеет место равенство
называется четной (нечетной), если имеет место равенство  (
(  ).
).
Область определения  четной или нечетной функции- симметрична относительно начала координат.
четной или нечетной функции- симметрична относительно начала координат.
График четной функции симметричен относительно оси Оу, а нечетной функции симметрична относительно начала координат
Функция не обладает четностью (не является ни четной и ни нечетной), так как ее область определения  -не симметрична относительно начала координат (
-не симметрична относительно начала координат (  но
но  ).
).
График функции не является симметричным относительно оси  и относительно начала координат О(0;0).
и относительно начала координат О(0;0).
Функция  называется периодической, если для некоторого числа
называется периодической, если для некоторого числа  имеет место равенство
имеет место равенство 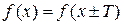
 .
.

 =>
=>
функция непериодична.
|
из
5.00
|
Обсуждение в статье: Исследование функции на четность и на периодичность |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

