 |
Главная |
ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ
|
из
5.00
|
№1
Упростить функцию, используя равносильные преобразования и определить ее тип. Выполнить проверку с помощью таблиц истинности:
1 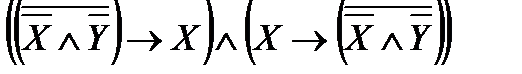
2 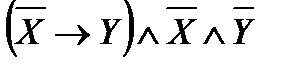
3 
4 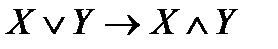
5 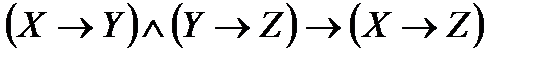
6 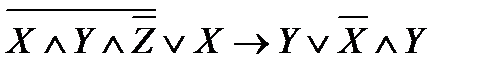
7 
8 
9 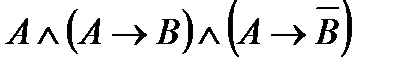
10 
11 
12 
13 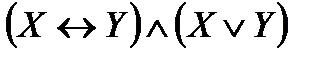
14 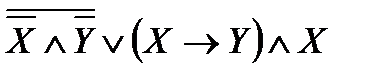
15 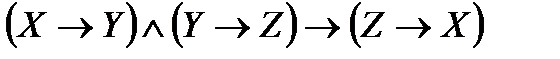
№2
На множестве М={1, 2,.., 20} заданы предикаты: А(x)={x не делится на 5}, В(x)= {x – четное число}, С(x)={x – число простое}, D(x)= {x – кратно 3}.
Найдите множество истинности следующего предиката:
1 С(x)Ù ØВ(x)
2 С(x)Ù ØD(x)
3 ØB(x) → D(x)
4 A(x)Ù В(x)Ù D(x)
5 A(x) → В(x)
6 ØB(x)Ù ØD(x)
7 ØB(x)Ù D(x)
8 A(x)→ ØD(x)
9 ØB(x)Ú D(x)
10 B(x)Ú ØD(x)
11 C(x)→ A(x)
12 D(x)→ ØC(x)
13 ØA(x)→ D(x)
14 ØB(x) Ù D(x)
15 ØC(x)→ A(x)
№3
Привести функцию к нормальным и совершенным
нормальным формам:
1 
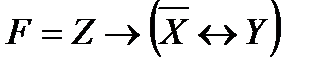
2 
3 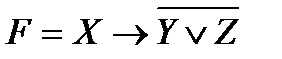
4 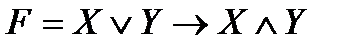
5 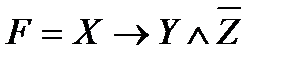
6 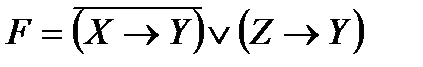
7 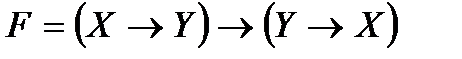
8 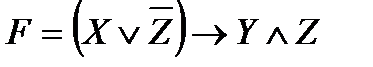
9 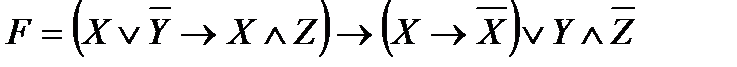
10 
11 
12 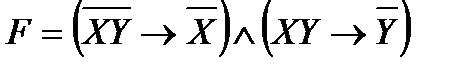
13 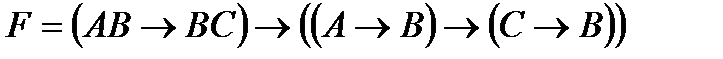
14 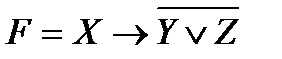
15 
№4
Осуществить операции над заданными множествами:
А∩F; АUF; А∩VUF; V\F; V\А; V\(F∩A); (V∩F)\A.
Изобразить полученные множества с помощью диаграмм Эйлера-Венна.
1 V={a, b, c, d, e, f}; А={a, b, c}, F={c, d, e, f}
2 V={p, q, w, e, r, d}; А={p, q, e}, F={w, q, r}
3 V={x, y, g, k, l, s}; А={x, y, k}, F={k, l, s}
4 V={1,3,5,7,9,11}; А={0,2,3,5}, F={0,1,2}
5 V={0,4,5,6,7,9}; А={4,5,7,9}, F={1,2,4}
6 V={3,4,6,7,8,9}; А={0,2,4,8,9}, F={2,5,8}
7 V={0,1,2,3,4,5}; А={2,4,8}, F={2,6,7,8}
8 V={3,4,6,8,9,13}; А={6,7,8}, F={0,2,6}
9 V={1,2,3,4,5,6}; А={3,6,7,}, F={3,7,0}
10 V={2,3,4,5,6,7}; А={4,7,8}, F={1,4,9}
11 V={3,4,5,6,7,8}; А={5,8,9}, F={4,8,1}
12 V={4,5,6,7,8,9}; А={1,6,9}, F={2,5,9}
13 V={1,3,5,7,9,11}; А={4,5,7,9}, F={0,1,2}
14 V={5,7,8,9,0}; А={0,5,7}, F={0,3,6}
15 V={3,4,6,8,9,13}; А={4,7,8}, F={2,5,9}
№5
Построить релейно-контактные схемы для F(x, y, z), если известны некоторые значения, а остальные значения функции F равны нулю. Упростить схему, если это возможно:
1 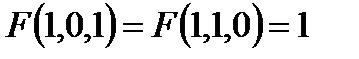

2 

3 

4 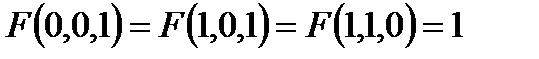

5 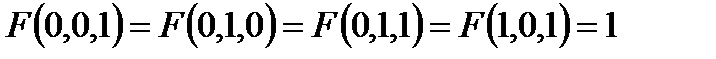

6 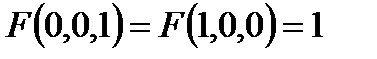
7 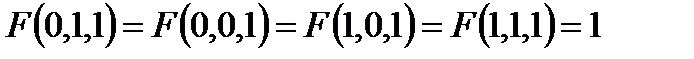
8 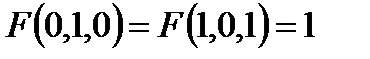
9 
10 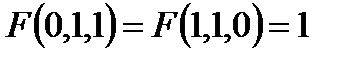
11 
12 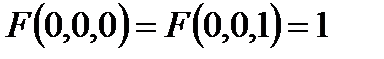
13 
14 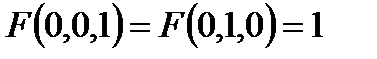
15 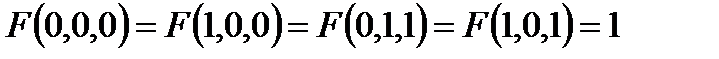
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЗАДАНИЙ
КОНТРОЛЬНОЙ РАБОТЫ
Теория алгебры логики
В математике и физики, в биологии и географии, в повседневной жизни мы постоянно встречаемся с различными утверждениями. Среди них есть утверждения истинные и ложные. В математической логике утверждения называются высказываниями. Алгебру логики иначе называют алгеброй высказываний.
Высказывание – это повествовательное предложение, о котором можно сказать, истинно оно или ложно (одновременно истинным и ложным высказывание быть не может)
В алгебре высказывания часто вместо символов используют логические значения высказываний. Если высказывание истинно, то его значение равно 1, если ложно – 0.
Сложное высказывание получаются путем объединения простых высказываний связками–союзами И, ИЛИ и частицей НЕ. Значение истинности сложных высказываний зависит от истинности входящих в них простых высказываний и от объединяющих их связок.
Логические связки в сложных высказываниях заменяются логическими операциями: конъюнкцией, дизъюнкцией и инверсией. Это основные логические операции, при помощи которых можно записать любую логическую функцию.
Конъюнкция двух логических переменных (элементарных высказываний
А и В) истинна тогда и только тогда, когда оба высказывания истинны
- соответствует союзу И
- обозначается знаками Ù, &
- иначе называется ЛОГИЧЕСКОЕ УМНОЖЕНИЕ
| - Определим все значения, которые могут принимать переменные - Используя определение конъюнкции, выпишем при каком наборе переменных, функция принимает истинное значение |
|
|
- соответствует союзу ИЛИ
- обозначается знаком Ú
- иначе называется ЛОГИЧЕСКОЕ СЛОЖЕНИЕ
Инверсия логической переменной истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна
-
|
- обозначается чертой над именем переменной 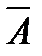 или
или 
- иначе называется ОТРИЦАНИЕ
Эквиваленция двух логических переменных истинна, если обе переменные истинны или ложны, и ложно, если одна из логических переменных истинна, а другая ложна
- соответствует словосочетанию «тогда и только тогда»
- обозначается знаком ~ 
- иначе называется РАВНОЗНАЧНОСТЬ
Импликация двух логических переменных ложна тогда и только тогда, когда из истины следует ложное высказывание
- соответствует словосочетанию «если, то»
- обозначается знаком Þ
-
|
|
Выражение, составленное из логических переменных с помощью операций над высказываниями и обращающееся в конкретное высказывание при подстановке вместо логических переменных конкретных высказываний, называется формулой высказываний.
Таким образом, появляется возможность применять логические операции многократно, получая с их помощью всё более сложные высказывания. При этом возникает одно затруднение: при записи сложных высказываний может оказаться неясным порядок, в котором следует проводить операции. Если формула не содержит скобки, то прослеживается следующий приоритет логических операций: инверсия, конъюнкция, дизъюнкция, импликация (эквиваленция).
Логические функции, истинные на всех наборах значений входных переменных, называются тождественно-истинными (тавтологией). Логические функции, ложные на всех наборах значений входных переменных, называются тождественно-ложными. Если у двух логических функций (формул) совпадают таблицы истинности, то есть на всех наборах значений входных переменных они принимают одинаковые значения, то их называют равносильными.
Равносильность высказываний можно устанавливать и другим способом, используя свойства, законы и формулы алгебры логики. Проводим цепочку равносильных преобразований, делая формулу более простой.
Свойства:
| конъюнкции | дизъюнкции | инверсии |

| 
| 
|

| 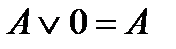
| |
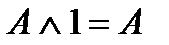
| 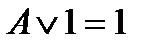
| |

| 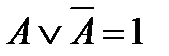
|
Законы:
| переместительные | сочетательные | распределительные | инверсии |
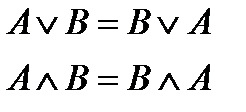
| 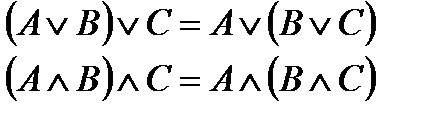
| 
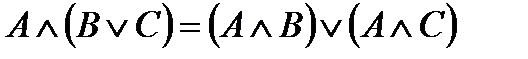
| 
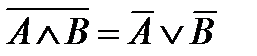
|
Формулы:
| склеивания | поглощения |
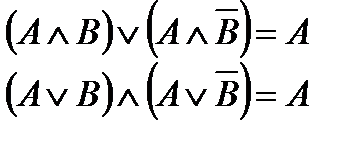
| 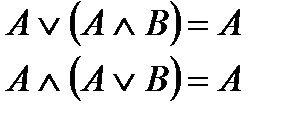
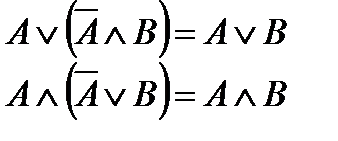
|
Задание.
Упростить функцию, используя равносильные преобразования и определить ее тип. Выполнить проверку с помощью таблиц истинности:
F= 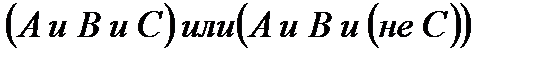
Решение:
1. Проводим цепочку равносильных преобразований, пока формула не станет минимальной:
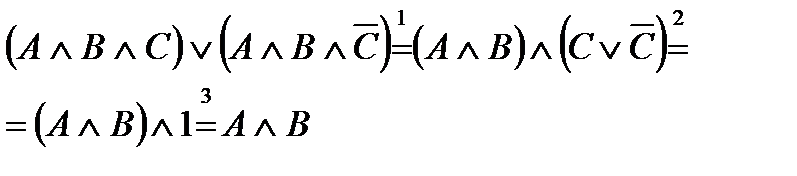
В ходе преобразовании использовали:
1) распределительный закон (вынесли общий множитель)
2) свойство дизъюнкции (закон исключения третьего)
3) свойство конъюнкции (умножение на 1)
2. Определяем тип заданной функции. Так как минимальная форма данной функции 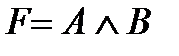 , то ее тип - конъюнкция переменных А и В.
, то ее тип - конъюнкция переменных А и В.
3. Используя таблицу истинности, выполним проверку нашего упрощения. Для построения таблицы истинности воспользуемся следующим алгоритмом:
1) Определим количество входных переменных (простых высказываний - 3) и по формуле 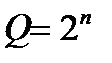 (n – количество переменных) вычислим количество строк (наборов переменных - 8)
(n – количество переменных) вычислим количество строк (наборов переменных - 8)
2) Методом половинного деления заполним значения входных переменных (первый столбец делим на две одинаковые группы 0 и 1, в каждом последующем столбце все группы вновь делятся на две одинаковые группы 0 и 1)
3) Проставим порядок действий и заполняем таблицу слева на право, где в каждом столбце по определению выполняем одну операцию алгебры логики. Последнее действие – это значения, которые принимает заданная функция на всех наборах переменных
| А | B | C | 
| А Ù B Ù С | А Ù B Ù 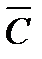
| (А Ù B Ù С)Ú( А Ù B Ù 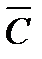 ) )
| А Ù B |
Значения заданной в условии задачи функции и полученного минимального выражения совпали на всех наборах переменных. Делаем вывод, что упрощение выполнено верно.
|
из
5.00
|
Обсуждение в статье: ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


 В
В
 В
В