Ожидаемая скорость скольжения, для данного задания

V_S ≈ 0,45 ∙10^-3∙ 750∙ 3,32 м/с.

С учетом указанных рекомендаций из таблиц 16, 25 [Р. 10] выбираем:

для червяка – сталь 40Х, термообработка улучшение и закалка ТВЧ, твердость поверхности зубьев 45…50 НRC (420…500 НВ), σ_Т = 750 Н/мм²;

для зубчатого венца колеса материал группы II – безоловянную бронзу марки БрА9ЖЗЛ, отливка в кокиль σ_Т = 195 Н/мм²; σ_В = 490 Н/мм².

 

4.3 Допускаемые контактные напряжения

Допускаемые контактные напряжения для материалов I группы определяются в следующей последовательности:

определяется общее число циклов перемены напряжений

N = 60n₂ ∙ t,

где t – ресурс работы редуктора, если по расчету N ≥ 25 ∙10⁷, то принимают N = 25 ∙10⁷;

коэффициент долговечности

К_HL = ;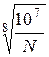

коэффициент интенсивности изнашивания зубьев С_V =1,66V_S^-0,352 или принимают в зависимости от скорости скольжения из следующего ряда:

VS, м/с				≥ 8
СV	0,95	0,88	0,83	0,8

 

Допускаемое контактное напряжение при числе циклов перемены напряжений, равным 10⁷

[σ]_НО = (0,75…9) σ_В,

где коэффициент 0,75 для червяков принимают при НRС < 45,

(НВ ≥350); 0,9 при НRС ≥45 (НB>350), а σ_В принимают по таблице 26 [Р. 10].

С учетом указанной последовательности, допускаемые контактные напряжения определяются по итоговой формуле

[σ]_Н = К_HL∙C_V[σ]_НО.

Для материалов группы II (таблица 26[Р. 10]) : [σ]_НО = 250 Н/мм² для червяков при НВ ≤ 350;

[σ]_НО = 300 Н/мм² для червяков при (НВ ≥ 350).

Допускаемые контактные напряжения

[σ]_Н = [σ]_НО – 25 V_S = 300-25∙3,32= 217 Н/мм².

III группа. Допускаемые контактные напряжения

[σ]_Н = 175 – 35 V_S.

 

4.4 Допускаемые изгибные напряжения

Допускаемые изгибные напряжения определяются по следующей методике:

определяется коэффициент долговечности

К_FL = ,

где N – число циклов нагружения;

рассчитывается исходное допускаемое напряжение изгиба по формулам таблицы 26 [Р. 10]:

для материалов I и II групп:

[σ]_Fo = 0,25σ_Т + 0,08σ_В;

для материалов III группы:

[σ]_Fo = 0,12σ_В

определяется расчетное допускаемое напряжение изгиба

[σ]_F = K_FL∙[σ]_Fo.

Для рассматриваемого примера, для материалов, выбранных ранее в п. 4.2, и в соответствии с предложенной методикой, определяются:

N = 60∙n₂ t = 60∙25∙30000 = 4,5∙10⁷ = 45∙10⁶;

К_FL = ≈ 0,66;

[σ]_Fo = 0,25∙195 + 0,08∙490=87,95 Н/мм², где значения σ_Т = 195 Н/мм² и

σ_В = 490 Н/мм², определенные ранее в п. 4.2;

[σ]_F = 0,66∙87,95 = 58,05 H/мм².

Для дальнейших расчетов принимаем

[σ]_Н = 217 Н/мм² и [σ]_F = 58,05 Н/мм².

 

4.5 Проектировочный расчет червячной передачи

На первом этапе проектировочного расчета из обеспечения условий прочности определяются основные геометрические параметры передачи.

4.5.1 Межосевое расстояние

Межосевое расстояние определяется из условия контактной прочности зубьев по формуле

a_ω ≥ 61 ,

где а_ω – межосевое расстояние;

61 – цифровой коэффициент червячной передачи.

Для рассматриваемого примера

a_ω ≥ 61 = 166,3 мм.

Рассчитанное значение a_ω необходимо привести к ряду нормальных чисел, в соответствии с таблицей 1 [Р. 10].

Стандартное значение межосевого расстояния a_ω = 170 мм.

 

4.5.2 Основные параметры передачи

Число заходов червяка z₁ зависит от передаточного числа u и определяется из следующего ряда чисел:

8 ≤ u ≤ 14; 14 < u < 30; u ≥ 30;

z₁ = 4; z₁ = 2; z₁ = 1.

Для рассматриваемого примера u =30, следовательно, z₁ = 1; число зубьев колеса z₂ = u·z₁ = 30·1 = 30. Выполняется условие z₂ > z_mίn = 28, чтобы не было подрезания зубьев.

 

Предварительное значение модуля передачи определяется по формуле:

m = (1,5…1,7) а_ω/z₂,

где m – предварительное значение модуля передачи,

m = (1,5…1,7) = 8,5…9,63 мм.

Полученное значение модуля округляют до стандартного модуля в соответствии с приведенным рядом стандартных модулей:

m, мм 2,5; 3,15; 4,0; 5,0; 6,3; 8,0; 10,0; 12,5; 16 (таблица 29 [Р. 10]).

Из этого ряда выбираем стандартное значение модуля m = 10 мм.

Предварительное значение коэффициента относительного диаметра червяка определяют по формуле:

q = .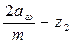

После подстановки в формулу рассчитанных цифровых значений получим

q = .

Минимальное допускаемое значение q из условия жесткости червяка проверяют по условию q_min = 0,212 · z₂ ; q_min = 0,212 · 30 = 6,36. Так как рассчитанное значение q = 4 меньше минимального допустимого q_min = 6,36, то для дальнейших расчетов принимают большее значение q, при рассчитанном модуле m = 10 мм q = 8 из таблицы 29 [Р. 10].

Для принятия окончательного решения о правильности расчетов и выбора параметров а_ω, z₂, q определяют коэффициент смещения х:

х = - 0,5 (z₂ + q) = 170/10 – 0,5(30+8) = 17 - 19= - 2.

Если по расчету |x| > 1, то изменяют значение а_ω,q илиz₂ из соответствующего ряда стандартных значений. Принимаем а_ω = 180 мм, m = 10 мм, q = 8. В этом случае

х = 180/10 – 0,5(30+8) = 18-19 = -1.

Так как значение |x| = 1, то принятые параметры а_ω, z₂, q не изменяются и нарезание зубьев производится без смещения инструмента.

Определяется значение фактического передаточного числа u_ф = z₂/z₁ = 30/1 = 30 и отклонение передаточного числа Δu от заданного

Δu = = ≤ 4%.

Следовательно, фактическое передаточное число соответствует заданному.

4.5.3 Геометрические размеры червяка и колеса

Определяются по стандартным формулам:

делительный диаметр червяка d₁ = mq = 10·8 = 80 мм;

диаметр вершин витков червяка d_a1 = d₁ +2m = 80+2·10 = 100 мм;

диаметр впадин d_f1 = d₁ – 2,4m = 80-2,4·10 = 56мм;

длина нарезанной части червяка при коэффициенте смещения x < 0

в₁ = (10+5,5 |x| +z₁) · m = (10 + 5,5 |-1| + 1) · 10 = 165 мм.

Полученное значение в ₁ округляют в большую сторону до стандартного числа из таблицы 1 [Р. 10], т.е. в₁ = 170 мм.

Примечание. При положительном смещении, т.е. х > 0, червяк должен быть несколько короче. В этом случае размер в₁, рассчитанный по приведенной выше формуле, уменьшают на величину (70 +60 · х)· m/z₂ и вновь полученное значение в₁ приводят к ряду стандартных чисел.

 

Диаметр делительной окружности колеса

d₂ = m·z₂ = 10·30 = 300 мм;

уточнение межосевого расстояния

а_ω = 0,5(d₁+d₂) = 0,5· (80 + 300) = 190 мм;

диаметр окружности вершин зубьев колеса

d_a2 = d₂ + 2(1 + x)· m = 300 + 2·10 = 320 мм.

Примечание. При уточненном значении а_ω величина коэффициента смещения х₁ определяется по формуле

х = = 190/10 – 0,5 (30 + 8) = 0;

диаметр колеса наибольший

d_am2 ≤ d_a2 +6m/(z₁ + 2) = 320 + 6∙10/1 +2 = 340 мм;

диаметр окружности впадин колеса

d_f2 = d₂ -2∙ m(1,2 – x) = 300 - 2∙10∙1,2 = 276 мм;

ширина венца колеса в₂ = ψ_ва · а_ω , где значение коэффициента ψ_ва принимается равным 0,355, если z₁ = 1 и 2; 0,315, если z₁ = 4,

в₂ = 0,355· 190 = 67,45 мм, полученное значение в₂ округляют в ближайшую сторону по таблице 1 [Р. 10], в₂ = 71 мм;

высота головки зуба h_a = m = 10 мм;

высота ножки зуба h_f = 1,2m = 1,2·10 = 12 мм;

высота зуба h = h_a + h_f = 10+12 = 22 мм;

шаг зацепления Р = π·m = 3,14·10 = 31,4 мм;

толщина зуба S, равная ширине впадин е, т.е. S = e = 0,5·P,

S = e =0,5 · 31,4 = 15,7 мм;

радиальный зазор С = 0,2· m = 0,2 · 10 = 2 мм;

угол наклона (подъема) линии витка червяка

γ = arctg [z₁ /(q + 2·x)] = arctg [1/8] = 7,125° (7°07').

После проведения расчетов основных геометрических параметров червяка, колеса и передачи в целом, определяют конструктивную форму колеса и червяка.

4.5.4 КПД передачи

КПД передачи рассчитывается с целью определения доли потерь энергии, затраченной на нагрев составных деталей редуктора.

КПД передачи определяется по формуле

η = 0,95 · ,

где р' – приведенный угол трения между червяком и колесом, принимают в соответствии со следующим рядом:

 

 

VS, м/с	0,5	1,0	1,5	2,0	2,5
р'	3°10' 3°40'	2°30' 3°10'	2°20' 2°50'	2°00' 2°30'	1°40' 2°20'	1°30' 2°00'	1°20' 1°40'	1°00' 1°30'	0°55' 1°20'	0°50' 1°10'

 

Меньшее значение угла р' - для оловянной бронзы, большее значение – для безоловянной бронзы, латуни и чугуна. Для определения значения угла р' необходимо предварительно определить уточненную скорость скольжения в зацеплении:

V_Sф = V₁/cosγ,

где V₁ – окружная скорость на червяке (V₁ = πd₁n₁/60000 м/с), а угол γ определен ранее в п. 4.5.3. Окружная скорость на колесе определяется по формуле: V₂ = πd₂n₂/60000 м/с.

Для рассматриваемого примера:

V₁ = 3,14·80·750/60000 = 3,14 м/с;

V₂ = 3,14·300·25/60000=0,39м/с;

V_Sф = 3,14/cos7⁰ 07' = 3,14/0,992 = 3,17 м/с.

V_Sф = 3,17 м/с отличается от предварительно принятой (смотри п.4.2) V_S = 3,32 м/с, поэтому [σ]_н = [σ]_но – 25V_s = 300 - 25·3,17 = 220,75 Н/мм².

По найденному значению скорости V_Sф из представленного ряда углов р' определяем необходимое значение р' = 1°54'. Подставляя найденное значение р'= 7° 07' в формулу для определения КПД, находим:

η = 0,95 .

Рассчитанное значение укладывается в интервал предварительно выбранных значений КПД.

 

4.5.5 Тепловой расчет передачи

Червячный редуктор в связи с невысоким значением КПД и большим выделением теплоты проверяют на нагрев. Условие работы редуктора без перегрева определяется:

t_раб ≤ [t_раб],

где t_раб – температура нагрева масла в °С, которая не должна превышать для широко применяемых масел 95°С.

Температура нагрева масла без искусственного охлаждения:

t_раб = [(1 – η)Р₁/К_тА]+20°С,

где Р₁ = πn₂Т₂/30η или Р₁ = Т₁ω₁ – мощность на валу-червяке Вт;

К_т = 12…18 Вт/м² °С – коэффициент теплоотдачи;

А – площадь поверхности охлаждения корпуса редуктора приближенно определяемая из прилагаемого ряда, как функция от межосевого расстояния а_ω по приведенной таблице или по таблице 32 [Р. 10]:

 

аω, мм
А, м2	0,19	0,24	0,36	0,43	0,54	0,67	0,8	1,0	1,2	1,4

 

После подстановки в указанные формулы, рассчитанных ранее значений, находим:

при а_ω = 190 мм А ≈ 0,735 м²

мощность на входном валу

Р₁ = = 3329,1 Вт;

температура нагрева масла при коэффициенте теплоотдачи

К_т = 12 Вт/м² °С

t_раб = [(1 – 0,75) · 3329,1/12·0,735]+ 20° ≈ 114°С.

Таким образом, условие работы редуктора без перегрева не выполняется, поэтому необходимо улучшить условия охлаждения. Этого можно достичь двумя конструкторскими решениями:

во-первых, увеличить поверхность охлаждения за счет дополнительных ребер на корпусе редуктора;

во-вторых, предусмотреть установку вентилятора и обеспечить принудительную вентиляцию редуктора, в этом случае расчет температуры нагрева производится по формуле:

t_раб = [(1-η)Р₁/(0,7К_т +0,3К_тв)·А]+ 20°С,

где К_тв – коэффициент теплоотдачи при обдуве вентилятором, выбирается в зависимости от числа оборотов вентилятора, который может быть установлен на входном валу редуктора, из следующего ряда:

n1
Ктв

 

Выбор способа улучшения охлаждения редуктора зависит от условий поставленной задачи. В рассматриваемом варианте решения задания приемлем любой способ, в частности при применении вентилятора температура нагрева масла определяется:

t_раб = С = 104…84°С.

Вывод. Обеспечение условий охлаждения редуктора достигается за счет установки вентилятора на входном валу редуктора и обеспечения хороших условий обдува (т.е. выбором большего значения коэффициента К_т).

 

4.5.6 Силы в зацеплении

В червячном зацеплении действуют окружная , радиальная и осевая силы , которые рассчитываются по формулам (рисунок 4.2):

окружная сила на колесе, равная осевой силе на червяке

F_t2 = F_a1= 2T₂/d₂ ;

окружная сила на червяке, равная осевой силе на колесе

F_t1 = F_a2 = 2T₂/(u · d₁ · η);

 

радиальная сила

F_r1 = F_r2 =F_t2 · tgα,

где α = 20° – стандартный угол зацепления; tg20° = 0,3640.

 

 

Рис. 4.2 Силы, действующие в червячном зацеплении

 

В рассматриваемом примере:

F_t2 = F_a1= Н;

F_t1 = F_a2= Н;

F_r1 = F_r2 = 6361,3· 0,3640 = 2315,5 Н.

 

4.5.7 Степень точности зацепления

Степень точности зацепления передачи принимают по таблице 20 [Р. 10] в зависимости от окружной скорости колеса. Окружная скорость колеса определена ранее в п. 4.5.4, V₂ = 0,39 м/с и в соответствии с таблицей 20 [Р. 10] степень точности зацепления пониженная 9-я.

4.6 Проверочный расчет зубьев колеса

Проверочный расчет передачи на прочность производится по контактным напряжениям и по напряжениям изгиба зубьев колеса. Червяки обычно выполняют за одно целое с валом, т.е. в виде вала-червяка, поэтому проверочный расчет на прочность и жесткость производится как для валов.

 

4.6.1 Проверочный расчет по контактным напряжениям

Условие прочности

σ_Н = (0,9…1,1) [σ_Н],

где σ_н – расчетное (фактическое) контактное напряжение, определяется по формуле

σ_Н = ,

где К_Н – коэффициент нагрузки, при V₂ ≤ 3 м/с К_Н =1,

а при V₂ > 3 м/с К_Н = 1,1…1,3.

Подставив в расчетную формулу исходные данные для рассматриваемого примера, имеем:

σ_Н = Н/мм².

Условие контроля по контактным напряжениям выполняется, так как

σ_Н = 174,8 Н/мм² меньше диапазона [σ_н] = 220,75…242,8 Н/мм².

[σ_Н] определено в п.4.3 и уточнено в п.4.5.4.

σ_Н = 174,8 Н/мм² < [σ_Н]= 220,75 Н/мм².

 

4.6.2 Проверочный расчет по напряжениям изгиба зубьев

Условие прочности

σ_F = ,

где Y_F – коэффициент формы зуба, принимается из ряда в зависимости от эквивалентного числа зубьев колеса по таблице 31 [Р. 10].

z_V2 = z₂/cos³γ,

коэффициент К_F был определен ранее в п. 4.6.1;

в₂ = 71 мм – ширина червячного колеса.

Для рассматриваемого примера, из результатов ранее рассчитанных параметров следует: К_F = К_Н = 1, и

z_V2 = 30/0,992³ = 30,73.

Этому значению соответствует Y_F = 1,71.

Тогда σ_F = Н/мм².

Условие прочности зубьев по напряжениям изгиба зубьев выполняется, так как σ_F = 10,72 Н/мм² << [σ]_F · 1,1 = 58,05 · 1,1 = 63,86 Н/мм².

Результаты расчета червячной передачи приведены в таблице 4.1

Таблица 4.1

Результаты расчета червячной передачи

 

Наименование параметров и размерность	Обозначение	Величина
Передаточное число	u
Допускаемое контактное напряжение, Н/мм2	[σ]Н	220,75
Допускаемые напряжения изгиба, Н/мм2	[σ]F	58,05
Межосевое расстояние, мм	а
Число заходов червяка	z1
Число зубьев колеса	z2
Модуль передачи (зацепления), мм	m
Относительный диаметр червяка	q	8,0
Диаметр делительный червяка, мм	d1
Диаметр вершин витков червяка, мм	dа1
Диаметр впадин витков червяка, мм	df1
Длина нарезной части червяка, мм	в1
Диаметр делительной окружности колеса, мм	d2
Диаметр окружности вершин зубьев колеса, мм	da2
Диаметр колеса наибольший, мм	dам2
Диаметр окружности впадин зубьев, мм	df2
Ширина зубчатого венца колеса, мм	в2
Высота головки зуба, мм	hа
Высота ножки зуба, мм	hf
Высота зуба, мм	h
Шаг зацепления, мм	р	31,4
Толщина зуба, мм	S = e	15,7
Угол наклона (подъема) линии витка червяка, град	γ	7° 07'
Скорость скольжения, м/с	Vs	3,17
КПД	η	0,75
Окружная сила на колесе, Н	Ft2 = Fa1	6361,3
Окружная сила на червяке, Н	Ft1 = Fa2
Радиальная сила, Н	Fr1 = Fr2	2315,5
Температура нагрева масла, °С	tраб	104…84
Расчетное контактное напряжение, Н/мм2	σH	174,8
Расчетное напряжение изгиба, Н/мм2	σF	10,72

 

4.7 Эскизное проектирование червячной передачи

Эскизное проектирование передач включает: определение размеров валов; выбор подшипников и схемы их установки; эскизное конструирование валов и компоновку передач редуктора; расчеты валов на прочность.

На рисунке 4.3 показана расчетная схема червячного редуктора для эскизного проектирования.

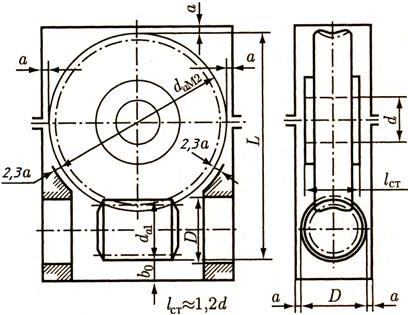
Рис. 4.3 Расчетная схема редуктора для эскизного проектирования

Основные конструктивные схемы валов и обозначений геометрических размеров показаны на рис. 3.1, 3.2,. Валы следует конструировать по возможности гладкими, с минимальным числом уступов, что приводит к существенному сокращению расхода металла на изготовление.

Для осевого фиксирования валов наиболее простой является схема установки подшипников «враспор».

Входной и выходной валы редукторов имеют консольные цилиндрические или конические участки для установки полумуфт.

Минимальные диаметры валов рассчитываются из условия только на кручение, как это было показано в сопротивлении материалов, по пониженным допускаемым касательным напряжениям [τ] по формуле:

d = ,

где [τ] = 15…30 Н/мм²;

Т - вращающий момент на валу в Н·м.

 

4.7.1 Проектировочный расчет входного вала и выбор подшипников

4.7.1.1 Расчетная схема. Исходные данные

Расчетная схема входного вала приведена на рис. 4.4.

 

 

Рис. 4.4 Расчетная схема входного вала

Входной вал В1 имеет цилиндрический консольный участок длиной ℓ_МБ и диаметром d, промежуточный участок длиной ℓ_КБ для установки подшипников и уплотнений диаметром d_П, участки диаметром буртика d_БП для упора во внутренние кольца подшипников, средний участок, представляющий червяк диаметром вершин витков червяка d_а1 и длиной нарезанной части в₁. Участок ℓ_МБ имеет наименьший диаметр, рассчитываемый из условия работы только на кручение, и служит для установки муфты Х1, соединяющей с валом электродвигателя.

Исходные данные: Т₁ = 45,44 Н·м; а _ω = 190 мм; d_а1 = 100 мм; d_f = 56 мм; в₁ = 170 мм; d_ам2 = 340 мм.

 

4.7.1.2 Геометрические размеры вала и выбор подшипников

Определение наименьшего диаметра вала из условия его работы только на кручение

d = = 22,5мм.

Этот диаметр согласуется с диаметром вала электродвигателя по условию

d= (0,7…1,0) d_э = (0,7…1,0) 42 = 29,4…42 мм.

Принимаем стандартное значение диаметра вала d = 30 мм

(таблица 1 [Р. 10]).