 |
Главная |
Показатели безотказности
|
из
5.00
|
Подробная версия.
Применение вероятностных схем. Вероятностные параметры оценки надежности и нарушения качества. Расчет последовательных, параллельных и комбинированных схем.
Основные понятия надежности
Надежность – один из показателей качества, однако часто этот показатель является основным, определяющим качество и эффективность продукции, в первую очередь технических объектов. Иногда обеспечение надежности есть главное условие безопасности работы объекта.
Под объектом понимается техническое изделие определенного назначения, например машины, сооружения, аппараты, приборы, их узлы и отдельные детали. Иногда в теории надежности объект рассматривается как система, состоящая из совокупности отдельных элементов, взаимодействующих между собой.
В соответствии со стандартом надежность – это свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонтов, хранения и транспортировки.
Состояние объекта, при котором он способен выполнять заданные функции, сохраняя значения основных параметров в пределах, установленных нормативно-технической документацией, называется работоспособностью. Состояние, при котором хотя бы один из указанных параметров не соответствует требованиям, – неработоспособность. Событие, состоящее в нарушении работоспособности, называется отказом. Процесс обнаружения и устранения отказа с целью перевода объекта из неработоспособного состояния в работоспособное называется восстановлением.
Иногда восстановление неработоспособного объекта невозможно или нецелесообразно. Предельное состояние объекта — это такое состояние, при котором дальнейшее применение объекта по назначению должно быть прекращено из-за неустранимого нарушения требований безопасности, неустранимого отклонения заданных параметров за установленные пределы, недопустимого увеличения эксплуатационных расходов или необходимости проведения капитального ремонта.
Продолжительность работы объекта называется наработкой. При работе объекта с перерывами учитывается суммарная наработка. Различают наработку до первого отказа, наработку между отказами и др. Наработка может измеряться как в единицах времени, так и в других единицах, например, циклах, километрах пробега и т.п. Наработка объекта от начала его эксплуатации до достижения предельного состояния называется техническим ресурсом. Срок службы объекта – это календарная продолжительность его эксплуатации от ее начала до наступления предельного состояния.
Надежность – комплексное свойство объекта, включающее его безотказность, ремонтопригодность, долговечность и сохраняемость.
Безотказность – свойство объекта непрерывно сохранять работоспособность в течение некоторого времени или наработки. Основными показателями безотказности являются вероятность безотказной работы, интенсивность отказов, средняя наработка до первого отказа и другие.
Ремонтопригодность – приспособленность объекта к предупреждению и обнаружению отказов, к восстановлению работоспособного состояния путем технического обслуживания и ремонта. Основные показатели ремонтопригодности – вероятность восстановления, интенсивность восстановления, среднее время восстановления, средняя наработка на отказ (отношение наработки восстанавливаемого объекта к математическому ожиданию числа отказов в течение этой наработки), коэффициент готовности (отношение времени, в течение которого объект находится в работоспособном состоянии, к обшей длительности периода) и другие.
Долговечность – свойство объекта сохранять работоспособность до наступления предельного состояния при установленной системе технического обслуживания и ремонта. Основные показатели долговечности – средний ресурс, гамма-процентный ресурс (наработка, в течение которой объект не достигает предельного состояния с заданной вероятностью 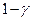 ), средний ресурс до капитального ремонта, средний срок службы и другие.
), средний ресурс до капитального ремонта, средний срок службы и другие.
Сохраняемость – свойство объекта сохранять работоспособное состояние после хранения и (или) транспортировки. Основные показатели сохраняемости – средний срок сохраняемости и гамма-процентный срок сохраняемости.
Показатели безотказности
Предполагается, что отказ – событие случайное, поэтому время работы объекта до первого отказа Т – случайная величина.
Вероятностью безотказной работы (или функцией надежности) называется вероятность события, состоящего в том, что время до первого отказа окажется не ниже некоторой заданной величины t, называемой наработкой до отказа.
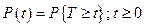 (1)
(1)
Естественно предположить, что в момент включения объект считается работоспособным: при t = 0 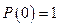 . С увеличением наработки t эта функция убывает до нуля (рис. 1).
. С увеличением наработки t эта функция убывает до нуля (рис. 1).
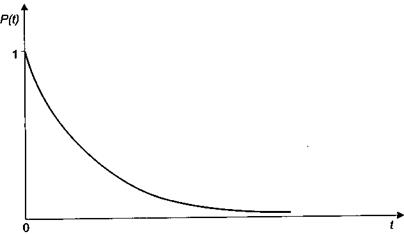
Рис. 1. Кривая вероятности безотказной работы
Вероятность того, что отказ произойдет до истечения заданного времени t называется вероятностью отказа. Отказ, очевидно, событие, противоположное работоспособности, поэтому вероятность отказа
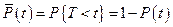 . (2)
. (2)
Нетрудно видеть, что вероятность отказа есть функция распределения случайной величины Т:
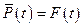 .
.
Если функция 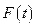 дифференцируема, то для характеристики безотказности может использоваться плотность распределения (рис. 1)
дифференцируема, то для характеристики безотказности может использоваться плотность распределения (рис. 1)
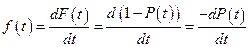 . (3)
. (3)
Учитывая, что
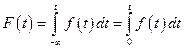 ;
;
соответственно
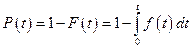 ,
,
получим
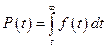 . (4)
. (4)
(использовано условие нормировки – площадь под кривой распределения равна единице).
Из формулы (4) следует, что вероятность безотказной работы соответствует площади под кривой распределения от заданного момента t до ∞ (на рис.2, б заштрихована). Элемент вероятности 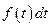 – это вероятность того, что случайная величина T примет значение, лежащее в пределах малого участка
– это вероятность того, что случайная величина T примет значение, лежащее в пределах малого участка 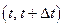 .
.
Средняя наработка до отказа есть математическое ожидание времени безотказной работы. Учитывая, что математическое ожидание непрерывной случайной величины определяется по формуле
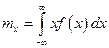
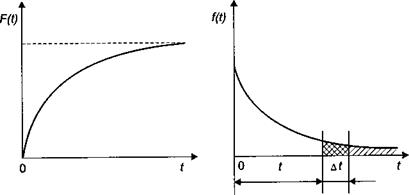
Рис. 2. Функция (а) и плотность распределения (б)
получим
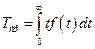 ,
,
но
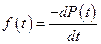 ,
,
тогда
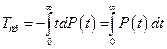 , (5)
, (5)
таким образом, средняя наработка на отказ численно равна площади под кривой вероятности безотказной работы 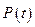 .
.
Используя формулы для дисперсии непрерывной случайной величины
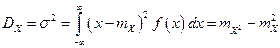 ,
,
можно по аналогии с (5) получить зависимость для дисперсии времени безотказной работы:
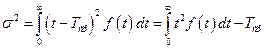 ,
,
откуда
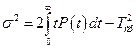 . (6)
. (6)
Предположим, что событие А = {отказ объекта при 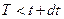 }, а событие В = {отказ объекта при
}, а событие В = {отказ объекта при 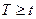 }. Вероятность
}. Вероятность
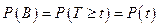
– это вероятность безотказной работы объекта. Тогда произведение этих событий АВ = {отказ в промежутке 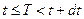 }, вероятность этого события
}, вероятность этого события
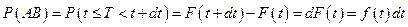
(использовано свойство функции распределения и определение плотности распределения). По формуле умножения вероятностей
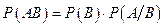 ,
,
здесь 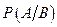 – вероятность отказа объекта в промежутке
– вероятность отказа объекта в промежутке 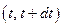 при условии, что он не отказал до момента t:
при условии, что он не отказал до момента t:
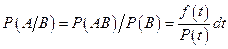 ;
;
эта вероятность пропорциональна отрезку времени dt, а коэффициент пропорциональности
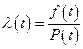 (7)
(7)
называется интенсивностью отказов. Отметим, что при 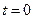
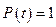 , поэтому
, поэтому 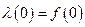 .
.
Пример 1
Вероятность безотказной работы изменяется по линейному закону, показанному на графике (рис. 3, а). Найти интенсивность отказов.
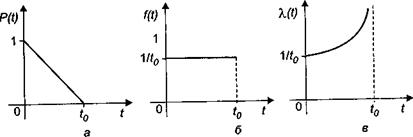
Рис. 3. Графики показателей надежности:
а – вероятность безотказной работы; б – плотность распределения;
в – интенсивность отказов
Уравнение прямой вероятности безотказной работы
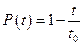 ,
,
тогда по формуле (3) плотность распределения
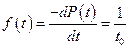 ,
,
т.е. постоянна (рис. 3, б).
Интенсивность отказов
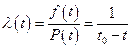 ;
;
соответствующая кривая – гипербола, при 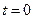
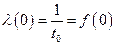 , при
, при 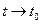
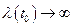 (рис. 3, в).
(рис. 3, в).
Выразим надежность через интенсивность отказов
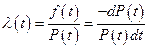 ,
,
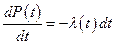 .
.
Интегрируя в пределах от 0 до t и учитывая, что 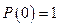 , получим
, получим
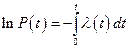 ,
,
или
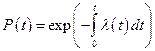 , (8)
, (8)
т.е. получили зависимость вероятности безотказной работы от интенсивности отказов.
В общем случае, как показывает опыт, график зависимости интенсивности отказов от времени (рис. 4) приближенно может быть представлен состоящим из трех участков: при 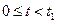 интенсивность отказов монотонно убывает – это период приработки, когда проявляются дефекты, обусловленные главным образом технологией изготовления объекта, при
интенсивность отказов монотонно убывает – это период приработки, когда проявляются дефекты, обусловленные главным образом технологией изготовления объекта, при 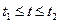 интенсивность постоянна (
интенсивность постоянна ( 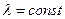 )– это период нормальной эксплуатации объекта; при
)– это период нормальной эксплуатации объекта; при 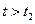 значения интенсивности снова возрастают – имеют место процессы старения.
значения интенсивности снова возрастают – имеют место процессы старения.
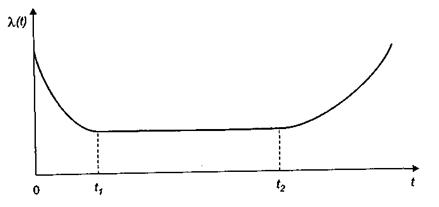
Рис. 4. Кривая интенсивности отказов
Кривую интенсивности отказов можно моделировать, используя различные виды распределения наработки до отказа. Наиболее распространенными являются экспоненциальное (рис. 5), нормальное и распределение Вейбулла.
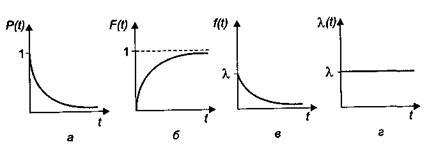
Рис. 5. Показатели надежности при экспоненциальном распределении:
а – вероятность безотказной работы; б – функция распределения;
в – плотность распределения; г – интенсивность отказов
В период нормальной эксплуатации интенсивность отказов практически постоянна: 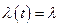 . Подставляя это соотношение в (8), найдем вероятность безотказной работы
. Подставляя это соотношение в (8), найдем вероятность безотказной работы
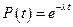 ;
;
тогда функция распределения (или вероятность отказов)
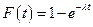
– это экспоненциальное распределение; плотность распределения
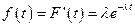 ,
,
средняя наработка до отказа:
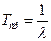 ,
,
дисперсия наработки:
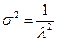 ,
,
с учетом зависимости для средней наработки до отказа вероятность безотказной работы может быть найдена по формуле
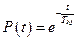 . (9)
. (9)
При использовании нормального распределения для моделирования отказов следует иметь в виду, что в обычном нормальном распределении случайная величина может меняться в промежутке от –∞ до ∞. Наработка до отказа – величина неотрицательная, поэтому используется усеченное нормальное распределение с плотностью
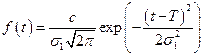 ,
,
где постоянная с определяется из условия нормировки:
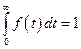 .
.
На практике обычно 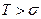 , тогда
, тогда 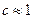 , в этом случае
, в этом случае 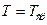 – средняя наработка до отказа,
– средняя наработка до отказа, 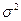 – дисперсия наработки. Имеем обычное нормальное распределение с плотностью
– дисперсия наработки. Имеем обычное нормальное распределение с плотностью
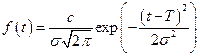 .
.
Функция нормального распределения может быть выражена через табулированную функцию стандартного нормального распределения
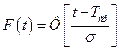 .
.
Вероятность безотказной работы:
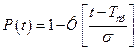 . (10)
. (10)
Используя полученные зависимости, можно выразить и интенсивность отказов (рис. 6). Из графиков видно, что нормальным распределением можно моделировать процессы старения, так как интенсивность отказов возрастает.
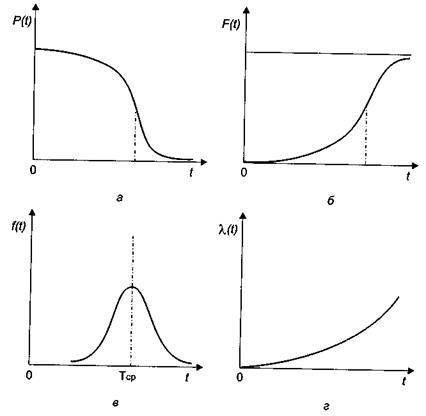
Рис. 6. Показатели надежности при нормальном распределении:
а – вероятность безотказной работы; б – функция распределения;
в – плотность распределения; г – интенсивность отказов
В практических расчетах для моделирования процессов старения иногда используется логнормальное распределение, в котором нормально распределенным предполагается логарифм случайной величины Т.
Более универсальным при моделировании отказов различных объектов является распределение Вейбулла (рис. 7). Это распределение можно рассматривать как обобщение экспоненциального распределения: функция распределения Вейбулла
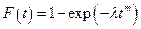 (11)
(11)
здесь 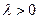 и
и 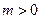 – параметры распределения, подбирая которые можно моделировать любой участок кривой интенсивности отказов.
– параметры распределения, подбирая которые можно моделировать любой участок кривой интенсивности отказов.
Вероятность безотказной работы:
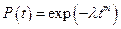 ; (12)
; (12)
плотность распределения:
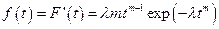 (13)
(13)
интенсивность отказов:
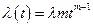 (14)
(14)
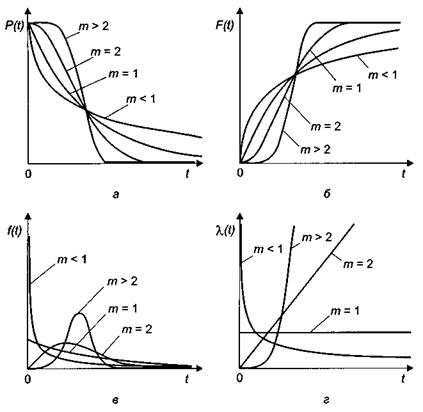
Рис. 7. Интенсивность отказов при распределении Вейбулла:
а – вероятность безотказной работы; б – функция распределения;
в – плотность распределения; г – интенсивность отказов
В частности при m = 1 имеем экспоненциальное распределение, при m = 2 – распределение Рэлея ( 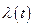 – наклонная прямая), при m < 1 моделируется участок приработки, при m > 2 – процессы старения.
– наклонная прямая), при m < 1 моделируется участок приработки, при m > 2 – процессы старения.
Пример 2
Наработка изделия до отказа имеет распределение Вейбулла с параметрами 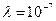 и m = 3. Найти вероятность безотказной работы в течение t = 102 ч.
и m = 3. Найти вероятность безотказной работы в течение t = 102 ч.
Имеем:
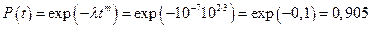 .
.
Для оценки характеристик надежности по опытным данным проводятся специальные испытания. По результатам испытаний принимается решение о виде распределения времени до отказа, оцениваются вероятность безотказной работы, интенсивность отказов, средняя наработка до отказа и другие характеристики.
Предположим, что наблюдается работа N однородных объектов, каждое изделие работает до отказа, регистрируются значения времени до отказа 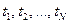 . Полученные значения разбиваются на интервалы длиной
. Полученные значения разбиваются на интервалы длиной 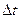 . Обозначим через
. Обозначим через 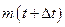 количество изделий, отказавших на участке времени
количество изделий, отказавших на участке времени 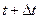 , а через
, а через 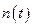 – количество изделий, оставшихся работоспособными к моменту времени t. Тогда оценка вероятности безотказной работы:
– количество изделий, оставшихся работоспособными к моменту времени t. Тогда оценка вероятности безотказной работы:
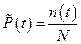 , (15)
, (15)
оценка плотности распределения (по гистограмме относительных частот):
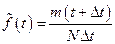 , (16)
, (16)
оценка интенсивности отказов:
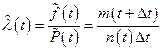 (17)
(17)
оценка средней наработки до отказа:
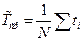
Пример 3
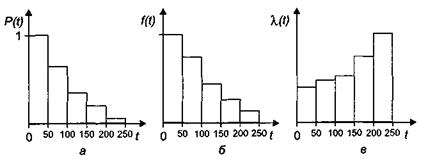
Испытано 100 лампочек. 42 перегорели в первые 50 ч. работы, 28 проработали от 50 до 100 ч., 16 – от 100 до 150, 10 – от 150 до 200, 4 – от 200 до 250 ч. Найти оценки характеристик надежности (табл. 2).
Taблица 2
| Наработка, ч. | 0 – 50 | 50 – 100 | 100 – 150 | 150 – 200 | 200 – 250 |
| |||||
| |||||
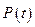
| 0,58 | 0,30 | 0,14 | 0,04 | |
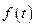
| 0,0084 | 0,0056 | 0,0032 | 0,0020 | 0,0008 |
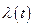
| 0,0084 | 0,00965 | 0,01067 | 0,01429 | 0,02 |
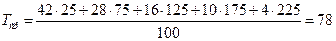 ч.
ч.
Графики характеристик надежности показаны на рис. 8.
| X(t) |
Рис. 8. Статистическая оценка показателей надежности:
а – вероятность безотказной работы; б – плотность распределения;
в – интенсивность отказов
По виду гистограммы относительных частот выдвигается гипотеза о виде распределения, проверяемая по одному из критериев согласия. Например, по критерию хи-квадрат вычисляется статистика
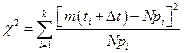 ,
,
где k – количество интервалов, 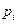 – расчетная вероятность попадания случайной величины в данный интервал:
– расчетная вероятность попадания случайной величины в данный интервал:
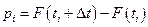 ,
,
где функция распределения 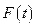 вычисляется в соответствии с предполагаемым распределением.
вычисляется в соответствии с предполагаемым распределением.
При экспоненциальном распределении
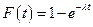
Для оценки параметра 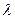 учитывается, что для экспоненциального распределения математическое ожидание – величина, обратная параметру
учитывается, что для экспоненциального распределения математическое ожидание – величина, обратная параметру 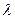 , т.е.
, т.е.
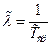 .
.
При нормальном распределении
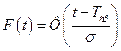 ,
,
где в качестве оценки дисперсии наработки используется
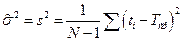 .
.
Гипотеза о предполагаемом распределении согласуется с опытом, если вычисленное значение 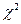 окажется меньше квантили, которое находится по таблице:
окажется меньше квантили, которое находится по таблице: 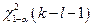 , где
, где 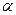 – уровень значимости, а l – количество неизвестных параметров, оцениваемых по выборке (для экспоненциального распределения
– уровень значимости, а l – количество неизвестных параметров, оцениваемых по выборке (для экспоненциального распределения 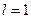 , для нормального
, для нормального 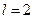 ).
).
В производственных условиях используют несколько различных типов испытаний на надежность. В зависимости от целей это могут быть определительные испытания, цель которых – оценка показателей надежности, и контрольные испытания для оценки уровня надежности исследуемого объекта. Контрольные испытания проводятся методами выборочного контроля при приемке продукции. В частности, широко используются методы последовательного контроля.
Испытания могут проводиться в лабораторных условиях или в условиях эксплуатации, при нормальной нагрузке и в ужесточенном режиме. Важной проблемой является длительность испытаний, поэтому часто применяют ускоренные испытания. Испытания характеризуются тремя параметрами:
– числом испытываемых изделий (N); в частном случае может испытываться и только одно изделие (N = 1);
– наличием или отсутствием восстановления (замены) вышедших из строя изделий (условное обозначение: М – восстановление, R – замена, U – без восстановления и замены);
– длительностью испытаний (условное обозначение: r – испытание до r-го отказа ( 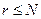 ), T – испытание длительностью Т, (
), T – испытание длительностью Т, ( 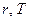 ) – испытание длительностью, равной
) – испытание длительностью, равной 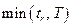 , где
, где 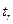 – момент r-го отказа, Т – заданный промежуток времени.
– момент r-го отказа, Т – заданный промежуток времени.
Соответствующие обозначения планов: [NMr], [NRr], [NUr], [NMT[, [NRT], [NUT], [NM(r, T)], и т.п. В частности, условное обозначение плана испытаний в приведенном выше примере: (N, U, r) при 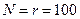 .
.
|
из
5.00
|
Обсуждение в статье: Показатели безотказности |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

