Надежность систем и резервирование

Рассмотрим надежность объекта, полагая, что он представляет собой систему, состоящую из n элементов. Введем следующие предположения:

– отказы элементов независимы (отказ одного из элементов не влияет на надежность других);

– состояние элементов системы однозначно определяет надежность всей системы;

– после отказа элементы не восстанавливаются.

Введем обозначения событий: событие А = {система надежна}, событие {j-й элемент надежен}.

Надежность j-го элемента

– это вероятность безотказной работы элемента за время t.

Вероятность отказа j-го элемента

.

Интенсивность отказов j-го элемента обозначим .

Надежность системы (вероятность ее безотказной работы):

.

Цель расчета – определение именно этого показателя. Вероятность отказа системы

.

Рассмотрим последовательное соединение элементов (рис. 9). Очевидно, система такого вида надежна тогда и только тогда, когда надежны все элементы (часто это обстоятельство принимают за определение последовательного соединения элементов): .

Рис. 9. Последовательное соединение элементов

С учетом независимости отказов надежность системы

, (18)

а вероятность отказа

.

Найдем интенсивность отказов системы:

.

При последовательном соединении интенсивность отказов системы равна сумме интенсивностей отказов ее элементов. При одинаковых надежностях элементов

, , , , .

Очевидно, при заданных вероятностях чем больше количество элементов в системе, тем ниже ее надежность. Например, при надежность системы из двух элементов составит:

,

из трех элементов:

и т.п.

При параллельном соединении (рис. 10) отказ системы произойдет тогда и только тогда, когда откажут все элементы:

;

вероятность отказа:

.

Тогда надежность системы:

. (19)

Рис. 10. Параллельное соединение элементов

Это обстоятельство используется для резервирования, когда для работы необходим один элемент, но его могут заместить другие в случае выхода этого элемента из строя.

Пример 4

Система состоит из двух последовательно соединенных элементов (рис. 11, а) с одинаковой надежностью . Сравнить надежность такой системы с надежностью резервированных систем: при общем резервировании (рис. 11, б) и поэлементном резервировании (комбинированная) (рис. 11, в).

Надежность системы по рис. 11, а найдена выше и составляет

.

Система по рис. 11, б – это параллельное соединение двух подсистем, каждая из которых состоит из двух последовательно соединенных элементов. Надежность каждой подсистемы равна , вероятность отказа , тогда в соответствии с формулой (19) получим

.

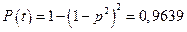Вероятность безотказной работы системы по рис. 11, в найдем как надежность двух последовательно соединенных подсистем. Надежность каждой подсистемы из двух параллельно соединенных элементов равна 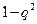, (здесь ); тогда надежность системы по формуле (18) составит:

.

Рис. 11. Расчет надежности систем при резервировании:

а – нерезервированная система;

б – система с общим резервированием;

в – система с поэлементным резервированием (комбинированная схема)

Резервные элементы могут быть постоянно нагружены, как и основной элемент; такой резерв называют нагруженным или горячим (именно такая ситуация рассмотрена в приведенном примере). Если же резервный элемент включается только при отказе основного элемента, то такой резерв называется холодным. Расчет холодного резервирования проводится с использованием аппарата теории марковских процессов.