Вопрос 20. Поле на границе раздела двух диэлектрических сред. Граничные условия для напряженности и вектора электростатической индукции электрического поля

Путь электрическое поле переходит из одного однородного диэлектрика в другой, который отличается только диэлектрической проницаемостью.

Разложим вектор Е₁ на две составляющие:

1) - перпендикулярную границе раздела диэлектрика.

2) - параллельную границе раздела диэлектрика.

Для того чтобы установить законы, согласно которым изменяются и 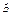при переходе воспользуемся теоремой о циркуляции вектора напряженности электрического поля и теоремой Гаусса.

Выберем контур который охватывает малую часть границы раздела. Стороны контура, параллельные границе раздела, имеют такую длину, что поле Е в ее пределах в каждом диэлектрике можно считать одинаковым, а высота контура пренебрежимо мала. Согласно теореме о циркуляции вектора Е:

(1)

При переходе электрического поля из одного диэлектрика в другой тангенциальная оказывается одинаковой по обе стороны границы раздела (не претерпевает скачка).

Условия для вектора .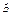

Возьмем очень малой высоты цилиндр, расположив его на границе раздела двух диэлектриков. Сечение цилиндра должно быть таким, чтобы в пределах каждого его торца вектор D был одинаков. Тогда согласно теореме Гаусса для вектора D: где 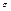- поверхностная плотность стороннего заряда на границе раздела. . Из этого соотношения видно, что нормальная составляющая вектора D претерпевает скачек при переходе границы раздела. Но если сторонние заряды на границе раздела отсутствуют ( ), то в этом случае нормальные составляющие вектора D скачка не испытывают, они оказываются одинаковыми по разные стороны границы раздела 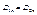(2). Таким образом, если на границе раздела двух однородных изотропных диэлектриков сторонних зарядов нет, то при переходе этой границы составляющие и 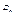изменяются непрерывно, без скачка. Составляющие же и претерпевают скачек.

Преломление линий Е и D.

Найдем соотношение между углами и 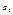. Если сторонних зарядов на границе раздела нет, то согласно (1) и (2) Из рисунка следует, что Отсюда с учетом предыдущих условий получаем закон преломления Е, а значит и D:

Это означает, что в диэлектрике с большим значением 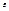линии Е и D будут составлять больший угол с нормалью к границе раздела.

Вопрос 21. Применение теоремы Гаусса для расчета электрических полей. Электрическое поле: 1) бесконечной равномерно заряженной плоскости; 2) вблизи заряженной металлической поверхности; 3) заряженного проводящего шара; 4) бесконечно равномерно заряженной нити; 5) однородно заряженного диэлектрического шара; 6) бесконечной равномерно заряженной по объему диэлектрической пластины конечной толщины.

1) Поле бесконечной равномерно заряженной плоскости. Пусть поверхностная плотность заряда . Благодаря равномерному распределению заряда по бесконечной плоскости, поле, созданное им, обладает плоской симметрией. Это означает, что линии электрического смещения 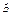направлены перпендикулярно плоскости. Кроме того, в симметричных относительно плоскости точках векторы 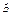одинаковы по модулю, но противоположны по направлению. Поток сквозь боковую поверхность цилиндра равен нулю, поэтому полный поток через всю поверхность цилиндра будет равен: , где 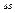- площадь каждого торца. Внутри цилиндра заключен заряд . Согласно теореме Гаусса откуда получаем выражение: 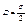, т.к. то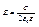

3) Поле заряженного проводящего шара.

Пусть заряд равномерно распределен по шару радиуса R. Поле такой системы центрально симметричное, поэтому для нахождения поля следует в качестве замкнутой поверхности взять концентрическую сферу.

1)

По теореме Гаусса:

Для точек сферы S1:

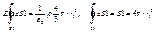
2)

Для точек сферы S2:

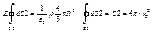
Формулы можно преобразовать с помощью:

4) Поле бесконечной равномерно заряженной нити.

Нить тонкая и равномерно заряженная. Заряд неподвижен. Поле обладает цилиндрической симметрией. На расстоянии R модуль напряженности электрического поля постоянен. Учитывая симметрию распределения заряда, в качестве гауссовской поверхности выберем цилиндр, геометрический центр которого совпадает с нитью. Длина образующей H. Радиус основания цилиндра R. - линейная плотность заряда. Согласно теореме Гаусса: . Полный поток вектора Е через цилиндр будет равен потоку через его боковую поверхность:

5) Поле однородно заряженного диэлектрического шара.

Расчет аналогичен полю заряженного проводящего шара. Для нахождения поля внутри шара нужно применить теорему Гаусса в виде . И за 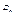принять

График зависимости Е от r поля равномерно заряженного диэлектрического шара. В рассмотренном случае диэлектрическая проницаемость вещества принята равной поэтому при перехода через поверхность шара напряженность скачкообразно меняется в 2 раза.

Вопрос 22. Электрическая емкость уединенного проводника. Емкость уединенного заряженного проводящего шара.

Рассмотрим процесс зарядки удаленного от других тел проводника. Сообщим ему заряд q. В результате этого заряд проводника станет равным . Этот заряд распределится по поверхности проводника так, чтобы напряженность поля внутри проводника стала равной нулю, а его поверхность стала эквипотенциальной. Пусть значение потенциала этой поверхности равно . Если теперь вновь сообщить проводнику такой же заряд q, то предыдущий заряд на проводнике не будет влиять на распределение нового заряда, так как внутри проводника напряженность поля 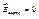. Следовательно новый заряд q распределится по поверхности точно так же, как и первый. В этом случае и заряд и потенциал проводника увеличится вдвое. При сообщении проводнику заряда q в n-ый раз все повторится: . Таким образом потенциал уединенного проводника будет все время пропорционален находящемуся на нем заряду .

где С – коэффициент пропорциональности называемый электроемкостью уединенного проводника. Физический смысл: (1). Электроемкость уединенного проводника численно равна заряду, который нужно сообщить этому незаряженному проводнику чтобы его потенциал стал равным единице . Единица емкости – фарад (Ф).

Емкость уединенного проводящего шара.

Радиус шара R. Шар находится в однородном и изотропном безграничном диэлектрике с проницаемостью 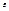. Сообщим шару заряд q и вычислим его потенциал (2).

Из (1) и (2) следует формула емкости уединенного проводящего шара:

Из этого выражения следует что электроемкость уединенного проводящего шара определяетя его размерами (R) и диэлектрическими свойствами среды, в которой он находится. В общем случае электроемкость уединенного проводника зависит также от его формы.